본 게시물은 문일철 교수님의 데이터 구조 및 분석을 참조하여 작성하였습니다.

배열 (Array)

배열(Array) 이란 기본적으로 동일한 자료형의 데이터를 인덱스를 활용하여 저장 및 접근할 수 있는 자료형입니다. 그렇기 때문에 배열의 각 요소에는 0부터 순차적으로 증가하는 인덱스가 할당되어 있습니다.

파이썬에서는 배열을 좀 더 일반화한 리스트(List)라는 자료형을 사용합니다. C, C++ 등의 언어는 배열에 들어가는 자료형의 종류와 배열의 크기를 미리 정해주어야 하지만 파이썬의 리스트는 이를 미리 지정하지 않고 리스트를 생성할 수 있습니다. 또한 리스트에서는 여러 자료형이 하나의 리스트에 들어가도록 할 수 있습니다.

x = ['a', 'b', 'd', 'e', 'f']

배열에서의 탐색(Search)

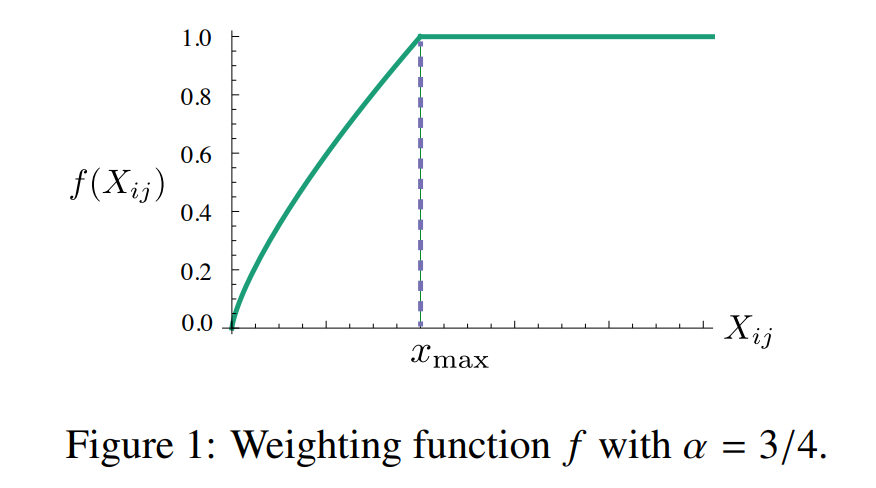
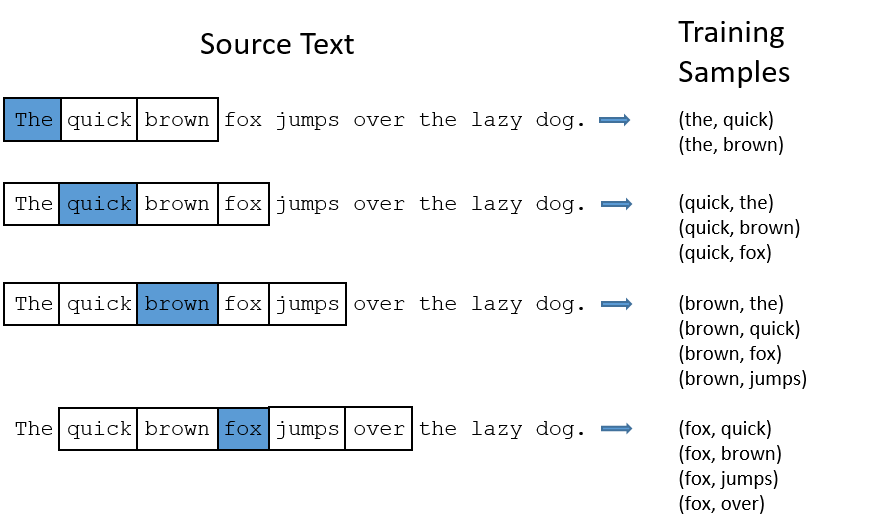
배열 안에 특정 요소가 있는 지를 탐색하는 알고리즘을 설계해 봅시다. 정렬된 배열의 경우 다른 알고리즘을 적용할 수도 있지만, 일반적인 경우는 0번째 인덱스부터 순차적으로 접근하여 그 값이 찾고자 하는 값인지 아닌 지를 비교합니다. 이를 선형 탐색(Linear search) 알고리즘이라고 합니다. 아래는 배열에서 선형 탐색 알고리즘이 이루어지는 과정을 도식화하여 나타낸 것입니다.

위에서 등장한 배열 x 에서 선형 탐색 알고리즘을 통해 'c' 와 'd' 를 찾는 과정을 생각해봅시다. 먼저 'c' 를 찾는 과정입니다. 우리는 'c' 가 없다는 것을 한눈에 알 수 있지만 컴퓨터는 한 번에 하나의 요소밖에 보지 못하므로 순차적으로 매 인덱스에 위치한 요소값을 확인하여 비교하여야 합니다. 알고리즘은 True 가 나올 때까지 진행되므로 배열 내에 없는 요소를 찾을 때는 모든 요소를 비교해야 합니다. 그렇기 때문에 배열의 길이인 $N$ 번의 Operation을 수행합니다. 이번에는 배열 안에 있는 'd' 를 찾는 과정입니다. 'c' 를 찾을 때와 같은 작업을 계속 반복하다가 해당 요소를 발견하면 종료합니다. 그렇기 때문에 찾고자 하는 값이 첫 번째로 있는 인덱스 (최대 $N$ 번)의 Operation을 수행하게 됩니다.

배열에서의 삽입(Insert)

이번에는 삽입 알고리즘 과정에 대해 생각해봅시다. 만약 위 배열 'b' 와 'd' 사이에 'c' 를 삽입하는 작업은 어떻게 할 수 있을까요? 배열에 특정 요소를 삽입할 때 원천적으로 발생하는 문제가 하나 있습니다. 위에서 배열은 크기가 정해져 있다고 했는데 어떻게 이미 만들어진 배열 안에 하나의 요소를 더 넣을 수 있을까요? 정담은 없습니다. 운전자 1명과 손님 4명이 타고 있는 택시에 손님을 태울 수 없는 것과 마찬가지입니다. 5명이 하나의 택시를 타려면 소형차가 아닌 중형보다 큰 새로운 차를 필요로 하는 것처럼, 배열도 정해진 개수보다 많은 요소를 삽입하려면 새로운 배열이 필요합니다.

우리의 목표는 하나의 요소를 삽입하는 것이므로 가장 먼저 원래의 배열보다 하나 더 큰 빈 배열을 만듭니다. 두 번째로는 새로운 요소를 삽입할 인덱스 이전까지의 참조(Reference)를 원래의 배열 x 에서 새로운 배열 y 로 복사합니다. 새로 삽입할 요소의 인덱스가 되면 그 참조를 우리가 삽입하고자 하는 값, 즉 'c' 에 연결합니다. 다시 다음 인덱스부터는 원래 배열 x 의 참조를 새로 만드는 배열의 하나씩 증가한 인덱스 y 에 복사합니다. 마지막으로 x 의 참조를 y 의 참조로 변경하면 삽입 과정이 완료됩니다. 아래는 이 과정을 도식화하여 나타낸 것입니다.

이 과정을 파이썬 코드로 구현하면 아래와 같습니다.

x = ['a', 'b', 'd', 'e', 'f']
idxInsert = 2
valInsert = 'c'

y = list(range(6))

for itr in range(0, idxInsert):
    y[itr] = x[itr]
    
y[idxInsert] = valInsert

for itr in range(idxInsert, len(x)):
    y[itr+1] = x[itr]
    
x = y

삽입 알고리즘에서는 Operation이 몇 번이나 일어날까요? 단계를 나누어 생각해봅시다. 원래 배열의 크기를 N, 새로운 요소를 삽입할 인덱스 idxInsert 를 a 라고 합시다. 그렇다면 그 0 부터 a-1 까지 참조를 복사하는 데 $a$ 번의 Operation을 수행합니다. 인덱스 a 에서 원하는 요소와 참조를 연결하는 과정에서는 $1$ 번의 Operation을 수행합니다. 인덱스 a+1 부터 N 까지의 참조를 복사하는 데에는 $N - a$ 번의 Operation을 수행합니다. 세 과정에서 수행하는 Operation의 개수를 합하면 삽입 알고리즘에 필요한 총 Operation 횟수가 $N + 1 = a + 1 + (N - a)$ 임을 알 수 있습니다.

배열에서의 삭제(Delete)

배열에서 특정 요소를 삭제하는 과정은 삽입 과정과 유사합니다. 배열에서 'd' 를 삭제하는 작업에 대해 생각해봅시다. 배열에는 빈자리도 있을 수 없으므로 하나의 요소를 삭제하기 위해서는 먼저 인덱스가 하나 적은 배열을 만들어야 합니다. 이후에는 삭제하려는 인덱스 이전에 있는 참조를 새로운 배열에 그대로 복사합니다. 삭제하려는 인덱스 이전에 있는 참조는 건너뛰게 되며 해당 인덱스 이후부터는 다시 새로운 배열의 하나씩 감소시킨 인덱스에 참조를 복사합니다. 마지막으로 원래의 배열 x 의 참조를 새로운 배열의 참조로 변경하면 삭제 과정이 완료됩니다.

이 과정을 파이썬 코드로 구현하면 아래와 같이 됩니다.

x = ['a', 'b', 'c', 'd', 'e', 'f']
idxDelete = 3

y = list(range(5))

for itr in range(0, idxDelete):
    y[itr] = x[itr]
    
for itr in range(idxDelete+1, len(x)):
    y[itr-1] = x[itr]
    
x = y

삭제 알고리즘에서는 Operation이 몇 번이나 일어날까요? 삽입과 마찬가지로 단계를 나누어 생각해봅시다. 원래 배열의 크기를 N, 삭제할 요소의 인덱스 idxDelete 를 b 라고 합시다. 그렇다면 그 0 부터 b-1 까지 참조를 복사하는 데 $b$ 번의 Operation을 수행합니다. 인덱스 b 에서는 아무런 Operation없이 건너뛰므로 고려하지 않으면 됩니다. 인덱스 b+1 부터 N 까지의 참조를 복사하는 데에는 $N - b$ 번의 Operation을 수행합니다. 세 과정에서 수행하는 Operation의 개수를 합하면 삭제 알고리즘에서는 총 $N + 1= b + 1 + (N - b)$ 회의 Operation이 필요함을 알 수 있습니다.

배열의 문제점

지금까지 알아본 것처럼 배열 속 요소를 탐색하는 과정 뿐만 아니라 새로운 요소를 삽입, 기존 요소를 삭제하는 작업을 위해서는 최대 $N$ 번의 Operation이 필요합니다. 배열 내에 수 개의 요소만 있을 경우에는 큰 상관이 없지만 배열의 크기 $N$ 이 $1,000,000$ 이상으로 매우 커지게 되면 삽입이나 삭제 과정에 그만큼의 Operation이 필요하므로 꽤 오랜 시간을 소모하게 될 것입니다. 선형 구조로 되어있는 배열은 삽입과 삭제에 불리합니다. 선형 구조에서는 크기가 $N$ 인 배열에 삽입 혹은 삭제를 수행하여 크기를 $N+1, N-1$ 로 만들 경우 모든 배열의 자리(인덱스)를 지정해 주어야 하기 때문입니다.

이런 문제를 개선하기 위해서는 선형 구조를 벗어나 새로운 자료구조의 세계로 들어가야 합니다. 이 자료구조에서는 삽입과 삭제를 오직 한 번의 Operation 만으로 수행할 수 있습니다. 그 자료구조가 바로 다음에 나올 연결 리스트(Linked List) 입니다.

본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 한국어 임베딩과 책의 저자인 Ratsgo님의 블로그를 참고하였습니다.

GloVe

Word2Vec에게도 단점이 있습니다. 시퀀스 내에 자주 사용되는 단어가 있으면 그 단어에 대해서 너무 많이 계산한다는 것입니다. 특히 아래는 위키피디아 - 대한민국의 첫 문단을 약간의 전처리 후에 형태소 분석한 것입니다.

“대한민국 은 동아시아 의 한반도 남부 에 있 는 민주 공화국 이 다 서쪽 으로 는 황해 를 사이 에 두 고 중화 인민공화국 이 동쪽 으로 는 동해 를 사이 에 두 고 일본 이 있 으며 북쪽 으로 는 조선 민주주의 인민공화국 과 맞닿 아 있 다 대한민국 의 수도 는 서울 특별시 이 고 실질 적 행정 수도 는 세종 특별자치시 이 다 국기 는 대한민국 국기법 에 따라 태극기 국가 는 관습 상 애국가 이 다 대한민국 내 에서 는 대한민국 을 간단히 한국 또는 남한 등 으로 도 부른다 조선 민주주의 인민공화국 에서 는 남조선 으로 불린다 대한민국 은 과거 엔 구한국 대한제국 과 구별 하 여 신 한국 이 라고 불리 기 도 하 였 다 연호 는 년 월 일 부터 서력기원 을 사용 한다”

위 문단에서 조사와 보조사인 “은”, “는”, “이”, “가”, “을”, “를” 등은 등장 횟수가 많기 때문에 학습 과정에서 해당 단어 시퀀스를 중복하여 계산하게 됩니다. 위 문단은 길이가 길지 않지만, 문단에서 ‘는’을 타겟 단어로 하는 시퀀스의 확률을 계산한다면 $P(\text{민주}\vert\text{는}), P(\text{황해}\vert\text{는}), P(\text{동해}\vert\text{는}), P(\text{조선}\vert\text{는}), P(\text{서울}\vert\text{는})$ 등 굉장히 많이 계산하게 될 것입니다.

서브샘플링(Sub-sampling)과 같은 기법을 활용하면 자주 등장하는 단어를 고의로 누락시켜 계산량을 보정해 줄 수는 있습니다만 완벽하게 문제를 해결하는 방법은 아닙니다. 이를 원천적으로 해결하기 위해서 등장한 방법이 GloVe(Global Vectors for word representation)입니다.

Glove는 행렬 분해법(Matrix factorization)에 기반하고 있습니다. 가장 먼저 동시 발생 행렬(Co-occurence)인 $X$를 만듭니다. $X$의 행과 열에는 말뭉치 내에 있는 모든 단어가 배치됩니다. 전체 단어의 개수가 $\vert V \vert$라면 $X$의 크기는 $\vert V \vert \times \vert V \vert$ 가 되겠습니다. 동시 발생 행렬 $X$의 성분인 $X_{ij}$ 는 $i$ 번째 행에 있는 단어가 $j$ 번째 열에 있는 단어와 함께 사용된 횟수를 나타냅니다. 즉 한 행의 성분인 $X_i$는 이를 전부 합친 것이므로 $i$ 번째 행에 있는 단어가 말뭉치 내에 등장한 횟수가 됩니다.

논문에서 사용한 예시를 통해서 Glove가 중복되는 시퀀스에 대한 계산을 보정하는 지를 알아보겠습니다. 아래 표는 특정 단어에 대하여 “ice”, “steam”이 각각 등장한 확률을 나타낸 것입니다. 표에 등장하는 조건부확률 $P(j\vert i)$, 즉 $i$ 단어가 주어졌을 때 $j$ 단어가 등장하는 확률을 구하는 식은 아래와 같습니다.

위 표에서 $P(\text{solid} \vert \text{ice}) = 1.9 \times 10^{-4}$라는 것은 “solid”와 “ice”가 동시에 등장한 횟수를 전체 말뭉치에 ice 라는 단어가 등장한 횟수로 나눈 것입니다. 이를 기억하며 표의 마지막 행에 집중해보겠습니다. $\frac{P(\text{solid} \vert \text{ice})}{P(\text{solid} \vert \text{steam})} = 8.9$ 는 무엇을 의미할까요?

(기준이 되는 단어가 다르기 때문에 횟수로는 비교할 수 없지만) 특정 문서에서 “solid”라는 단어가 등장하는 빈도는 “steam”보다 “ice”가 등장했을 때 더 높음을 나타냅니다. 즉 “solid”는 “ice”와 더 깊은 관련이 있다는 것이지요. 반대로 “gas”는 마지막 행의 수치가 $\ll 1$ 이므로 “ice”보다 “steam”과 함께 더 자주 등장하는 것으로 보아 “steam”과 더 깊은 관련이 있음을 알 수 있습니다. “water”와 “fashion”는 마지막 행의 수치가 $\approx 1$이므로 “ice”든 “steam”이든 등장하는 빈도에 별 차이가 없다는 것을 알 수 있습니다.

Objective Function

Glove의 목적 함수(Objective function)가 어떻게 구해지는지 알아보겠습니다. 위 3번째 행을 일반화한 $\frac{P(k \vert i)}{P(k \vert j)}$를 각각의 단어 $w_i, w_j, \tilde{w_k}$ 를 파라미터로 하는 함수 $F$로 나타내보겠습니다. $\tilde{w}$ 는 주변 단어에 대한 벡터, 즉 문맥(Context) 벡터를 나타냅니다.

기준이 되는 두 단어의 관계는 두 단어의 차인 $w_i - w_j$로 표현합니다. 또한 기준이 되는 두 단어와 타깃 단어 $w_k$ 에 대한 관계는 내적으로서 나타내기로 합니다. 이를 적용하면 $F$의 인자를 세 단어 벡터가 결합된 하나의 항으로 변형시킬 수 있습니다.

[F(w_i, w_j, \tilde{w}_k) = F(w_i - w_j, \tilde{w}_k) = F((w_i -w_j)^T \cdot \tilde{w}_k)]

이 $F$ 를 이용하여 표 3행 2열에 있는 성분, $\frac{P(\text{solid} \vert \text{ice})}{P(\text{solid} \vert \text{steam})}$ 와 역수를 나타내면 아래와 같이 나타낼 수 있습니다.

[\begin{aligned} \frac{P(\text{solid} \vert \text{ice})}{P(\text{solid} \vert \text{steam})} &= F((\text{ice} - \text{steam})^T\text{solid})
\frac{P(\text{solid} \vert \text{steam})}{P(\text{solid} \vert \text{ice})} &= F((\text{steam} - \text{ice})^T\text{solid})
\therefore F((\text{ice} - \text{steam})^T\text{solid}) &= \frac{1}{F((\text{steam} - \text{ice})^T\text{solid})} \end{aligned}]

준동형 사상(Homomorphism)이라는 방법을 사용하여 함수 $F$의 형태를 유추해볼 수 있습니다. 아래 수식을 통해서 함수 내의 변수는 덧셈에 대한 역원 관계에 있고, 함숫값은 곱셈에 대한 역원관계가 있음을 알 수 있습니다.

[\begin{aligned} (\text{ice} - \text{steam})^T\text{solid} &= - (\text{steam} - \text{ice})^T\text{solid}
F((\text{ice} - \text{steam})^T\text{solid}) &= \frac{1}{F((\text{steam} - \text{ice})^T\text{solid})}
\therefore F(a+b) &= F(a)F(b) \end{aligned}]

즉, $F$는 임의의 $a,b$에 대하여 $F(a+b) = F(a)F(b)$를 만족합니다. 이 조건을 만족하는 함수 중 가장 간단한 형태는 $e^x$ 형태의 지수함수(Exponential function)입니다. $F(x) = \exp(x)$로 두고 식을 변형시킬 수 있습니다.

[\begin{aligned} F\bigg((w_i-w_j)^T \cdot \tilde{w_k}\bigg) &= \frac{F(w_i^T\tilde{w_k})}{F(w_j^T\tilde{w_k})}
\exp(w_i^T\tilde{w_k}-w_j^T\tilde{w_k}) &= \frac{\exp(w_i^T\tilde{w_k})}{\exp(w_j^T\tilde{w_k})} \end{aligned}]

$P_{ik} = \exp(w_i^T\tilde{w}_k)$ 이므로 식을 다음과 같이 변형할 수 있습니다.

[\begin{aligned} w_i^T\tilde{w}k = \log P{ik} &= \log X_{ik} - \log X_i
\because P_{ik} &= \frac{X_{ik}}{X_i}
\end{aligned}]

$\log X_i$ 는 상수이므로 2개의 상수의 합 $b_i+ \tilde{b_k}$ 로 치환하여 나타낼 수 있습니다. 치환 후에는 다음과 같이 식이 변하게 됩니다.

[\begin{aligned} w_i^T\tilde{w}k &= \log X{ik} - b_i - \tilde{b_k}
w_i^T\tilde{w}k + b_i + \tilde{b_k} &= \log X{ik} \end{aligned}]

위 식을 이용하여 GloVe의 목적 함수(Objective function)를 다음과 같이 쓸 수 있습니다. 여기서 마지막 항에 해당하는 $\log X_{ij}$는 데이터셋을 통해서 이미 알고있는 것이고 나머지 $w_i, \tilde{w_j}, b_i, \tilde{b_j}$는 학습이 되는 미지수입니다.

[J = \sum_{i,j=1}^V (w_i^T\tilde{w}j + b_i + \tilde{b_j} - \log X{ij})^2]

목표는 이 오차를 최소화 시키는 것이므로 $\text{argmin}_{w,b} J(w,b)$ 가 됩니다. 논문에서는 알고리즘의 성능을 높이기 위해서 목적 함수에 동시 발생 행렬의 원소를 인자로 가지는 하나의 함수 $f$ 를 더 적용했습니다.

논문에서 함수 $f$가 만족해야 하는 조건으로 제시한 것은 3가지 입니다. 첫 번째로 $f(0) = 0$ 이어야 합니다. 두 번째로는 동시 발생 횟수가 적은 단어에 과한 가중치를 부여하지 않기 위해서 증가 함수여야 합니다. 세 번째는 동시 발생 횟수가 높은 단어에도 과한 가중치를 부여하지 않기 위해 상대적으로 적은 값을 적용하는 함수여야 합니다. 이 모든 조건을 만족하는 함수로 논문에서 제시한 함수는 다음과 같습니다.

[f(x) = \begin{cases} \big(\frac{x}{x_\text{max}}\big)^\alpha \quad \text{ if} \quad x < x_\text{max}\ 1 \qquad \qquad \text{otherwise}\end{cases}]

$\alpha = 0.75$일 때, 위 함수의 그래프는 아래와 같습니다. 이 함수를 적용한 목적함수 $J$ 는 그 아래 수식과 같이 변하게 되어, 최종적인 $J$ 를 줄이는 것을 목표로 학습하게 됩니다.

이미지 출처 : lovit.github.io

[\Rightarrow J = \sum_{i,j=1}^V f(X_{ij})(w_i^T\tilde{w}j + b_i + \tilde{b_j} - \log X{ij})^2]

Fasttext

지금까지 등장했던 확률기반 신경망 모델(NPLM), Word2Vec, GloVe는 단어가 가진 형태적 특성을 무시하고 있다는 한계점을 가지고 있습니다. 이런 문제 때문에 형태소 변화가 다양한 언어인 터키어나 핀란드어에는 잘 작동하지 않는다는 단점을 가지고 있습니다. 예를 들면, 다음과 같은 것입니다.

터키어 단어 : “çevrenizdekilere” = “çevreniz + de + ki + ler + e” (5개 형태소의 합)

핀란드 단어 : “sanoinhan” = “sano + i + n + han” (4개 형태소의 합)

이렇게 하나의 단어가 여러 가지 형태소의 합으로 되어있는 경우에는 형태소 분석을 제대로 해주지 않는다면 제대로 된 임베딩을 하기가 어렵습니다. Fasttext는 이런 한계점을 극복하기 위해서 고안된 방법입니다. Fasttext는 단어 혹은 형태소 단위가 아니라 캐릭터(Character,철자) 단위로 접근합니다. 이를 서브워드(Subword) 모델이라고도 합니다.

Fasttext는 그럼 하나의 단어를 어떻게 표현하는 것일까요? 각 캐릭터의 N-gram 표현을 벡터로 나타내며 이 벡터들의 합을 단어로 표현합니다. $N = 3, 4, 5, 6$ 일 때의 캐릭터 시퀀스를 만들어 각각에 임베딩 벡터를 부여한 뒤 원래 단어를 포함한 벡터까지의 합을 한 단어의 임베딩 벡터로 계산합니다. 위에서 예를 들었던 “sanoinhan”이라는 단어가 Fasttext에서는 어떻게 임베딩 되는 지를 보겠습니다. Fasttext에서는 양 옆에 ”<”,”>“을 붙여 단어를 구분합니다.

<sanoinhan>을 $N = 3$ 으로 나눈 캐릭터 시퀀스는 ”<sa”, “san”, “ano”, … ,”an>“으로 총 11개가 있습니다. 원래 단어는 sanoinhan 입니다.

총 12개의 벡터를 더하여 단어의 최종 임베딩 벡터로 사용합니다. (물론 4, 5, 6-gram 캐릭터 시퀀스까지 적용하면 갯수가 더 많아집니다.) 아래 그림에서도 “eating”이라는 단어를 3-gram의 캐릭터로 자른 뒤에 원래 단어와의 합을 통해 단어 임베딩 벡터를 나타내고 있습니다.

이미지 출처 : amitness.com

Fasttext에 서브워드 모델을 적용할 수 있는 바탕에는 Word2Vec의 목적 함수가 있습니다. 네거티브 샘플링을 사용한 Word2Vec의 목적 함수는 다음과 같았습니다.

[J_t(\theta) = \log \sigma(u_o^Tv_c) + \sum^k_{i=1}E_{i \sim P(w)}[\log \sigma(-u_i^Tv_c)]]

위 식을 보면 각 시그모이드 함수에 들어가는 파라미터, 즉 Score는 임베딩 벡터와 가중치 벡터의 내적으로 이루어져 있는 것을 알 수 있습니다. 그래서 서브워드 모델에서도 Score를 다음과 같이 두 벡터의 내적 값을 모든 시퀀스에 대해 더하여 도출합니다. $G_w (\subset {1, \cdots , G})$는 단어 내에 등장하는 모든 캐릭터 시퀀스입니다.

[\text{score}(w,c) = \sum_{g \in G_w} \mathbf{z}_g^T\mathbf{v}_c]

Fasttext는 Score를 계산하는 방법만 다를 뿐이지 나머지 목적 함수에 대해서는 네거티브 샘플링을 적용한 Word2Vec 모델과 동일합니다.

위에서도 설명한 것처럼 Fasttext는 단어의 형태 변화에 대해 강건(Robust)합니다. 아래처럼 단어의 원형에 다른 접미사 등이 붙더라도 서브워드로 분리하기 때문에 좋은 성능을 보여줍니다.

이미지 출처 : amitness.com

이런 특징 덕분에 교착어¹인 한국어에 적용하여도 꽤 높은 임베딩 성능을 보인다는 장점을 가지고 있습니다.

본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 책을 참고하였습니다.

Word2Vec

지난번 게시물에 있었던 확률기반 신경망 언어 모델(NPLM)은 처음으로 단어 임베딩을 언어 모델에 사용하였습니다. 이번에는 단어 임베딩에서 가장 많이 쓰이는 모델인 Word2Vec에 대해서 알아보겠습니다. Word2Vec에는 크게 CBoW(Continuous Bag-of-Words)와 Skip-gram의 2가지 방법이 있습니다.

CBoW & Skip-gram

NPLM에서도 가정했던 것처럼 Word2Vec의 두 방법 CBoW와 Skip-gram은 모두 “특정 단어 주변에 있는 단어는 유사한 관계를 맺고 있을 것이다”라는 전제를 하고 있습니다. 이런 전제에 따라

결정적인 차이는 학습의 기준이 되는 단어와 학습할 단어의 차이에 있습니다. 윤동주 시인의 시를 통해서 CBoW와 Skip-gram이 어떻게 학습을 해가는지를 알아보겠습니다. 아래는 Mecab 으로 추출한 별헤는 밤의 형태소 일부입니다.

“… 어머님 나 는 별 하나 에 아름다운 말 한마디 씩 불러 봅니다 …”

이 가사를 CBoW를 활용하면 아래의 빈칸에 들어갈 단어를 예상하는 과정으로 학습이 진행됩니다.

“… 나 는 [ __ ] 하나 에 … “

“… 는 별 [ ____ ] 에 아름다운 …”

“… 별 하나 [ __ ] 아름다운 말 …”

“… 하나 에 [ _________ ] 말 한마디 …”

Skip-gram을 진행하면 다음의 빈칸에 들어갈 단어를 예상하는 과정으로 학습이 진행되지요.

“… [ __ ] [ __ ]별 [ ____ ] [ __ ] …”

“… [ __ ] [ __ ]하나 [ __ ] [________ ] …”

“… [ __ ] [ ____ ] 에 [ _________ ] [ __ ] …”

“… [ ____ ] [ __ ] 아름다운 [ __ ] [ ______ ] …”

위 처럼 CBoW는 주변 단어(Context)를 보고 타겟 단어 $w_t$ 를 예측하게 되고, Skip-gram은 타겟 단어 $w_t$ 를 보고 주변 단어 $C$ 를 입력하게 됩니다. 얼핏 생각해보면 더 많은 정보를 받아서 단어를 예측하는 CBoW의 성능이 좋을 것으로 생각하기 쉽습니다. 실제로는 Skip-gram 방법이 역전파를 통해 더 많은 학습 정보를 받을 수 있습니다. 아래는 학습이 되는 과정을 도식화한 이미지입니다.

이미지 출처 : researchgate.net

위 그림을 역전파의 관점에서 생각해보면 CBoW는 타겟 단어 $w_t$의 학습 정보를 주변 단어 4개가 모두 나누어 받게 됩니다. 반대로 Skip-gram은 타겟 단어 $w_t$ 가 무려 주변 단어 4개의 학습 정보를 받게 됩니다. 실제로 Skip-gram이 성능이 더 좋지만 하나의 타겟 단어를 학습하는데 4단어에 대한 학습을 진행하므로 시간이 더 오래 걸리고 더 많은 컴퓨팅 자원을 필요로 한다는 단점이 있습니다.

Structure

실제로는 모델의 성능 덕분에 CBoW보다는 Skip-gram이 더 많이 사용됩니다. 그렇기 때문에 이번 게시물에서는 Skip-gram을 중심으로 어떻게 학습이 진행되는 지를 알아보겠습니다. 일단 Skip-gram 모델의 기본적인 구조는 아래와 같이 생겼습니다.

이미지 출처 : mccormickml.com

가장 왼쪽에 있는 입력 벡터는 원-핫 인코딩을 거친 벡터로 우리가 알고 있는 타겟 단어만 $1$ 로 표시됩니다. 총 10,000개의 단어가 있을 때 300차원으로 임베딩 하기 위해서는 아래와 같은 가중치 행렬(Weight matrix, 주황색)가 필요하게 되고 이를 참조(Lookup)하여 단어 임베딩 벡터로 이루어진 행렬(파란색)을 만들게 됩니다.

이미지 출처 : mccormickml.com

임베딩을 마친 단어 임베딩 벡터는 출력층에서 소프트맥스 함수를 통해서 주변 단어를 각각 예측하게 됩니다.

이미지 출처 : mccormickml.com

실제 학습과정에서는 4개의 단어를 한꺼번에 학습 하는 것이 아니라 (타겟단어, 주변단어)처럼 타겟 단어와 각 주변 단어의 쌍을 만들어 각각을 학습합니다. 아래 이미지는 모델에서 이런 방식으로 학습 샘플을 만드는 것을 잘 나타내는 그림입니다.

이미지 출처 : mccormickml.com

Skip-gram with Gradient Ascent

Skip-gram의 목적 함수 $J(\theta)$를 다음과 같이 나타낼 수 있습니다. $\theta$ 는 파라미터 행렬이며 $t$ 는 각 타겟 단어인 $w_t$ 를 가리킵니다.

그럼 이 목적함수를 바탕으로 Skip-gram에서 경사 상승법을 통해 학습이 진행되는 과정을 살펴보겠습니다. 수식의 단순화를 위하여 $w_{t+j} \rightarrow o, w_t \rightarrow c$(outside, center)로 나타내면 주변 단어의 확률을 아래와 같이 나타낼 수 있습니다.

위 확률을 최대화하는 것이 목적입니다. 타겟 단어마다의 목적 함수 $J_t(\theta)$ 와 $\text{argmax}$ 를 사용하면 식을 아래와 같이 나타낼 수 있습니다.

확률을 최대화 하는 $v_c$를 찾는 것아야 하기 때문에 $v_c$로 편미분한 식을 $0$ 으로 만드는 $v_c$를 찾아야합니다. 수식으로 알아보도록 하겠습니다.

[\begin{aligned} \frac{\partial}{\partial v_c} \log p(o|c) &= \frac{\partial}{\partial v_c} \log \frac{\exp(u_o^Tv_c)}{\sum^W_{w=1} \exp(u_w^Tv_c)}
&= \frac{\partial}{\partial v_c} u_o^Tv_c-\frac{\partial}{\partial v_c} \log \sum^W_{w=1} \exp(u^T_w v_c)
&= u_o - \frac{1}{\sum^W_{w=1} \exp(u^T_w v_c)} \cdot \sum^W_{w=1} \exp(u^T_w v_c) \cdot u_w
&= u_o - \sum^W_{w=1}\frac{\exp(u^T_w v_c)}{\sum^W_{w=1} \exp(u^T_w v_c)} \cdot u_w
&= u_o - \sum^W_{w=1} P(w|c) \cdot u_w \end{aligned}]

확률을 최대화 하는 것이 목적이므로 경사 상승법(Gradient Ascent)을 적용하여 가중치 벡터 $v_c$ 를 개선해나가게 됩니다.

Skip-gram with Sampling

Skip-gram의 단점은 계산량이 많아 시간이 오래 걸린다는 점입니다. 아무런 처리가 없을 때, $V$개의 단어를 가진 말뭉치를 $N$차원의 임베딩 벡터로 학습하려면 $2\times V\times N$ 만큼의 가중치를 학습해야 합니다. 위 그림처럼 “brown”이 타깃 단어이고 주변 단어에 “fox”가 있을 때 (brown, fox)로 학습하고, “fox”가 타깃 단어이고 주변 단어에 “brown”이 있을 때에는 (fox, brown)을 학습하기 때문입니다. 이를 위해 고안된 샘플링(Sampling) 기법은 중요도가 떨어지는 단어의 개수를 줄임으로써 임베딩 벡터의 성능을 떨어뜨리지 않으면서도 계산량을 줄일 수 있도록 하는 방법입니다.

Sub-sampling

서브샘플링(Sub-sampling)은 자주 등장하는 단어를 학습 대상에서 제외하는 방법입니다. 아래 식에서 $P(w_i)$는 단어 빈도 $f(w_i)$ 에 따라서 이 값이 높은 단어를 누락시키는 확률입니다. $t$ 는 임계값(threshold)입니다.

[P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}}]

예를 들어, 총 말뭉치에 등장하는 단어 중 10,000번에 1번 등장하는 단어 $w_1$이 학습에서 누락될 확률과 100번에 1번 등장하는 단어 $w_2$가 학습에서 누락될 확률을 비교해봅시다. 이 때 $t = 10^{-5}$ 로 설정하겠습니다.

[\begin{aligned} P(w_1) &= 1 - \sqrt{\frac{10^{-5}}{10^{-4}}} = 1 - \sqrt{\frac{1}{10}} = 0.6838 \qquad \because f(w_1) = \frac{1}{10000} = 10^{-4}
P(w_2) &= 1 - \sqrt{\frac{10^{-5}}{10^{-2}}} = 1 - \sqrt{\frac{1}{1000}} = 0.9684 \qquad \because f(w_2) = \frac{1}{100} = 10^{-2} \end{aligned}]

위 식을 보면 $w_1$ 은 말뭉치에 100번 등장할 때 약 68개의 단어가 누락되므로 32개의 단어만 학습에 사용됩니다. 하지만 $w_2$ 는 말뭉치에 1000번이나 등장하더라도 968개의 단어가 누락되므로 32개의 단어만 학습에 사용됩니다. 이렇게 서브샘플링을 하면 자주 나오는 단어들에 대한 확률을 급격히 낮춤으로써 계산량을 줄일 수 있습니다.

Negative Sampling

네거티브 샘플링을 설명하기 위해서 위에서 사용했던 Skip-gram의 구조 이미지를 다시 가져와 보겠습니다.

이미지 출처 : mccormickml.com

이 구조에 따르면 총 10,000단어에 대한 300개의 임베딩 벡터를 학습하기 위해서 소프트맥스 단계의 행렬의 요소는 $10,000 \times 300 = 3,000,000$개가 됩니다. 각각의 요소를 경사 상승법으로 반복해서 학습하기에는 너무 많은 양이지요. 네거티브 샘플링(Negative Sampling)은 수많은 파라미터 중 일부만을 학습하기 위해 고안된 전략입니다.

네거티브 샘플링 전략을 사용하지 않았을 때는 타겟 단어 $w_t$와 주변 단어 중 하나인 $w_o$에 대하여 학습 샘플이 $(w_t, w_o)$로 계산됩니다. 결국 하나의 계산마다 $w_o$를 구할 때 10,000개 단어 전부를 예측의 대상으로 하기 때문에, 소프트맥스의 계산량이 매우 많습니다. 네거티브 샘플링은 예측 대상을 포지티브 샘플(Positive sample) $1$개와 네거티브 샘플(Negative sample) $k$개로 구성함으로써 소프트맥스 계산을 줄일 수 있습니다.

위에서 포지티브 샘플은 $w_o$ 에 해당하는 단어이고, 네거티브 샘플은 $w_o$에 해당하지 않는 단어입니다. 위에서 했던 <별 헤는="" 밤="">을 예시로 다시 가져와 보겠습니다.

… 어머님 나 는 별 하나 에 아름다운 말 한마디 씩 불러 봅니다 소학교 때 책상 을 같이 했 던 아이 들 의 이름 과 패 경 옥 이런 이국 소녀 들 의 이름 과 벌써 애기 어머니 된 계집애 들 의 이름 과 가난 한 이웃 사람 들 의 이름 과 비둘기 강아지 토끼 노새 노루 프란시스 쟘 라이너 마리아 릴케 이런 시인 의 이름 을 불러 봅니다 …

위에서 첫 번째 줄에 있는 “아름다운” 이라는 단어를 학습한다고 해봅시다. 왼쪽과 오른쪽 각각 2개의 단어를 예측할 때 포지티브 샘플에 해당하는 단어는 “하나”, “에”, “말”, “한마디” 입니다. 이 네 단어를 제외한 모든 단어는 Negative sample에 해당합니다. 즉 네거티브 샘플링을 사용하면 예측 대상이 전체 단어의 개수인 10,000개에서 $k+1$ 개로 줄어듭니다. 이렇게 샘플링한 후에는 $k+1$ 개 각각의 학습 세트에 대해 이 세트가 포지티브 샘플인지 네거티브 샘플인지를 예측하는 이진 분류(Binary classification) 작업을 수행합니다.

일반적으로 학습 데이터가 작은 경우에는 $5 \leq k \leq 20$ 정도가 적당하며, 말뭉치가 클 때는 $2 \leq k \leq 5$ 정도로 조정합니다. 예를 들어, “아름다운”을 타겟 단어로 하여 $k = 5$로 네거티브 샘플링하여 학습한다고 하면 학습 데이터셋을 아래와 같이 구성하게 됩니다. 아래 표에서 $w_t$ 는 타겟 단어이며 $w_p$ 는 각 포지티브 샘플이고, $w_{n}$ 은 각각의 네거티브 샘플입니다.

각각에 대해 이진 분류를 수행하므로 $k = 5$인 경우에는 $(1+5) \times 300 = 1,800$ 개가 됩니다. 학습해야 할 파라미터의 개수가 $3,000,000 \rightarrow 1,800$ 로 매우 많이 줄어든 것을 볼 수 있습니다.

그런데 네거티브 샘플을 구성하는 단어는 어떤 기준으로 뽑는 것일까요? 논문에서는 말뭉치에 자주 등장하지 않는 단어에 가중치를 줄 수 있도록 네거티브 샘플 확률을 설정하였습니다. $f(w_i)$를 말뭉치의 단어 $w_i$가 등장할 빈도라고 할 때 네거티브 샘플이 될 확률 $P(w_i)$은 아래와 같습니다.

[P(w_i) = \frac{f(w_i)^{3/4}}{\sum_{j=0}^n (f(w_i)^{3/4})}]

예를 들어, 전체 말뭉치가 4개의 단어 $w_1, w_2, w_3, w_4$로만 구성되어 있고 각 단어의 빈도는 $f(w_1) = 0.1, f(w_2) = 0.2, f(w_3) = 0.3, f(w_4) = 0.4$ 라고 해봅시다. 이 때, 각 단어가 네거티브 샘플로 뽑힐 확률은 다음과 같습니다.

[\begin{aligned} P(w_1) = \frac{0.1^{3/4}}{0.1^3/4+0.2^3/4+0.3^3/4+0.4^3/4} = 0.1284
P(w_2) = \frac{0.2^{3/4}}{0.1^3/4+0.2^3/4+0.3^3/4+0.4^3/4} = 0.2159
P(w_3) = \frac{0.3^{3/4}}{0.1^3/4+0.2^3/4+0.3^3/4+0.4^3/4} = 0.2926
P(w_4) = \frac{0.4^{3/4}}{0.1^3/4+0.2^3/4+0.3^3/4+0.4^3/4} = 0.3631 \end{aligned}]

빈도가 적은 $w_1, w_2$ 는 원래 단어의 빈도보다 네거티브 샘플이 될 확률이 늘어나는 것을 볼 수 있고, 빈도가 높은 $w_3, w_4$ 는 원래 단어의 빈도보다 낮게 계산되는 것을 볼 수 있습니다.

네거티브 샘플링을 사용하면 각 이진 분류에 대해 시그모이드 함수 $\sigma$ 를 활성화 함수로 사용하게 됩니다. 네거티브 샘플링을 사용하여 변화된 타겟 단어 마다의 목적 함수 $J(\theta)$는 다음과 같이 변하게 됩니다.

[J_t (\theta) = \log \sigma(u_o^T v_c) + \sum_{i=1}^T E_{i \sim P(W)} \big[\log \sigma(-u_i^T v_c)\big] \]

Word Pairs or Phrases to Word

계산량을 줄이는 마지막 방법으로 통상적으로 쓰이는 관용어구를 하나의 단어로 취급하는 방법이 있습니다. 예를 들어, “Boston Globe”(신문사 이름)과 같은 고유명사나 “this is” 처럼 통상적으로 쓰이는 관용어구를 하나의 단어로 처리합니다.

본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 책을 참고하였습니다.

Distributed Representation

지금까지 알아본 Bag of Words, TF-IDF, N-gram 방법론은 단어를 등장 횟수 기반으로 벡터로 표현(Count-based representation)하는 방식이었습니다. 이번에는 등장 횟수가 아닌 단어의 분산 표현(Distributed representation)방법에 대해 알아볼 것입니다.

횟수 기반 표현을 사용하지 않고 단어를 벡터화하는 가장 단순하고 직관적인 방법은 원-핫 인코딩(One-hot Encoding)입니다. 원-핫 인코딩은 적용하는 방법은 다음과 같습니다. 일단 문서에 존재하는 단어의 개수 만큼의 차원을 가진 영벡터를 만듭니다. 그리고 단어가 등장하는 순서에 따라 해당 인덱스를 1로 변환한 뒤 그 단어의 벡터로 매칭시켜줍니다. 예를 들어, “What’s your name? My name is Yngie.” 라는 문장에 있는 단어를 원-핫 인코딩을 사용하여 벡터로 표현하면 다음과 같습니다.

[\begin{aligned} \text{what} : \left[{\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \end{array}}\right]
\text{is} : \left[{\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \end{array}}\right]
\text{your} : \left[{\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \end{array}}\right]
\text{name} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right]
\text{my} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 1 & 0 \end{array}}\right]
\text{Yngie} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 1 \end{array}}\right] \end{aligned}]

원-핫 인코딩은 단순하고 이해하기 쉽다는 장점이 있습니다. 하지만 단어끼리의 관계를 모사할 수가 없게 됩니다. 벡터 간 유사도를 판단하는 방법은 다양하지만, 단어 벡터 사이의 유사도를 판단하는 데에는 주로 코사인 유사도(Cosine similarity)가 사용됩니다. 코사인 유사도의 수식은 다음과 같습니다.

[\text{similarity}(\vec{x},\vec{y}) = \frac{\vec{x} \cdot \vec{y}}{\Vert\vec{x}\Vert \Vert\vec{y}\Vert} = \frac{x_1y_1 + \cdots + x_ny_n}{\sqrt{x_1^2+\cdots+x_n^2} \sqrt{y_1^2+\cdots+y_n^2}}]

원-핫 인코딩으로 생성된 임의의 서로 다른 두 단어 벡터 $\vec{x_o}, \vec{y_o}$ 의 단어간 유사도를 구하기 위해 코사인 유사도 식에 대입하면 어떻게 될까요? 결과만 보자면 모두 0이 나오게 됩니다. 원-핫 인코딩으로 생성된 서로 다른 벡터를 내적한 값 $\vec{x_o} \cdot \vec{y_o}$ 은 언제나 0이 나오기 때문입니다. 이 때문에 원-핫 인코딩은 단어의 의미 관계를 전혀 표현하지 못하게 됩니다.

이런 문제를 해결하기 위해서 분산 표현 방식인 단어 임베딩(Word Embedding)이 고안되었습니다. 임베딩은 단어를 문서 내 단어의 개수 $\vert V \vert$보다 훨씬 작은 숫자인 $n$ 차원의 벡터로 나타냅니다. 임베딩을 통해 나타내어지는 단어 벡터는 성분이 0, 1이 아닌 연속적인 숫자로 구성되어 있습니다. 그렇기 때문에 단어 벡터끼리 내적하여도 0이 아니게 되며 단어 간의 의미(Semantic) 관계가 보존된다는 장점을 가지고 있습니다. 아래 그림은 임베딩을 통해 추출해낸 단어 벡터 간의 관계를 시각화한 것입니다.

이미지 출처 : towardsdatascience.com

Neural Probabilistic Language Model

확률론적 신경망 언어 모델(Neural Probabilistic Language Model, NPLM)은 기존 단어 횟수 기반의 언어 모델(Language models)의 단점을 극복하고자 만들어진 방법입니다.

신경망 언어 모델에서 각 단어는 임베딩을 통해 $n$ 차원의 벡터로 표현됩니다. 이 단어 벡터를 언어 모델에 적용했을 때의 장점은 무엇일까요? 기존의 언어 모델은 횟수를 기반으로 등장 확률을 결정하기 때문에 말뭉치에 한 번도 등장하지 않은 시퀀스에 대해서는 등장 확률이 0이 된다는 단점이 있었습니다. 예를 들어, “마라룽샤를 요리하다.” 라는 단어 시퀀스가 말뭉치에 등장하지 않는다면 이 시퀀스가 생성될 확률 역시 0이 됩니다.

하지만 임베딩을 통해 표현된 단어 벡터는 의미 관계를 가지고 있기 때문에 다릅니다. 예를 들어, (마라탕, 마라샹궈, 마라룽샤)라는 세 단어묶음, (요리하다, 먹다) 의 관계가 비슷하다고 학습한 모델이 있다고 합시다. 이 모델은 말뭉치에 “마라탕을 먹다” 라는 시퀀스만 있더라도 “마라샹궈를 먹다, 마라탕을 요리하다, 마라룽샤를 먹다, 마라룽샤를 요리하다” 등 다양한 단어 시퀀스를 생성할 수 있게 됩니다. 이제 더 이상 말뭉치 시퀀스에 집착하지 않아도 되는 것이지요.

모델 학습

확률론적 신경망 언어 모델은 기본적으로 N-gram 방식을 사용하여 단어를 추론합니다. 즉, 타겟 단어의 확률을 구하기 위한 조건으로 이전 $N-1$ 개의 단어 벡터를 고려합니다. 아래 그림은 모델의 구조를 이미지로 나타낸 것입니다.

이미지 출처 : imgur.com

먼저 입력 벡터 신경망에 들어갈 $\mathbf{x_t}$ 가 어떻게 생성되는지 알아보겠습니다. 이 과정은 커다란 행렬 $C$ 에서 타겟 단어인 $w_t$ 를 참조(look-up)하는 방식으로 이루어집니다. 위 그림에서도 각 단어인 $w$ 에 맞는 행을 참조 $C(w)$ 하여 벡터화하는 것을 볼 수 있습니다. 전체 $\vert V \vert$ 개 단어 모두를 $n$ 차원 벡터로 나타내기 위해 참조하는 것이므로 $C$ 의 크기는 $\vert V \vert \times n$ 이 됩니다.

실제의 연산은 모든 단어를 원-핫 인코딩을 통해 원-핫 벡터 $w_t$ 로 나타낸 뒤에 $C$ 와 내적하는 과정으로 이루어집니다. 원-핫 인코딩에서 사용했던 “What’s your name? My name is Yngie.” 문장을 예시로 다시 가져와보겠습니다.

[\begin{aligned} \text{what} : \left[{\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \end{array}}\right]
\text{is} : \left[{\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \end{array}}\right]
\text{your} : \left[{\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \end{array}}\right]
\text{name} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right]
\text{my} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 1 & 0 \end{array}}\right]
\text{Yngie} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 1 \end{array}}\right] \end{aligned}]

이 단어를 5차원 벡터로 나타내려면 참조할 행렬 $C$ 의 사이즈는 어떻게 되어야 할까요? 단어의 개수 $\vert V\vert = 6$ 이고 나타내고자 하는 임베딩 벡터의 차원 $n = 5$ 이므로 $6 \times 5$ 가 되어야 하겠습니다. 행렬 $C$ 의 성분은 정해져 있는 것이 아니고 초기에 임의의 값을 넣어준 후 학습 과정에서 갱신되는 것이므로 임의의 값을 넣어 만들어 보겠습니다.

[C : \left[{\begin{array}{ccccc} 10 & 2 & 3 & 2 & 4 \ 4 & 9 & 7 & 3 & 5 \ 1 & 4 & 11 & 3 & 7 \ 7 & 7 & 5 & 4 & 2 \ 9 & 8 & 3 & 2 & 5 \ 8 & 2 & 3 & 1 & 7 \end{array}}\right]]

단어의 원-핫 벡터 $w_t$ 와 $C$ 를 내적하면 각 단어의 벡터 $\mathbf{x}_t$ 를 구할 수 있게 됩니다. $C$ 의 각 행이 단어 벡터가 되는 것을 알 수 있습니다. 예를 들어, “name” 의 임베딩 벡터 $\mathbf{x}_4$ 가 만들어지는 과정을 보겠습니다.

[\left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right] \cdot \left[{\begin{array}{ccccc} 10 & 2 & 3 & 2 & 4 \ 4 & 9 & 7 & 3 & 5 \ 1 & 4 & 11 & 3 & 7 \ 7 & 7 & 5 & 4 & 2 \ 9 & 8 & 3 & 2 & 5 \ 8 & 2 & 3 & 1 & 7 \end{array}}\right] = \left[{\begin{array}{ccccc} 7 & 7 & 5 & 4 & 2 \end{array}}\right]]

N-gram 방식을 사용하여 타겟 단어의 확률을 예측하기 때문에 입력 데이터는 $N-1$ 개의 단어 벡터가 됩니다. 예를 들어, “What’s your name? My name is Yngie.” 라는 문장에서 첫 번째 “name” 을 Tri-gram, 즉 $N=3$ 으로 예측한다면 “is, your” 의 임베딩 벡터를 입력하게 되므로 입력 데이터는 다음과 같아집니다. 아래 식에서 $\mathbf{x_2}, \mathbf{x_3}$ 는 각각 “is” 와 “your” 의 임베딩 벡터를 나타낸 것입니다.

[\therefore \mathbf{x} = [\mathbf{x}_2, \mathbf{x}_3] = [\left[{\begin{array}{ccccc} 4 & 9 & 7 & 3 & 5 \end{array}}\right], \left[{\begin{array}{ccccc} 1 & 4 & 11 & 3 & 7 \end{array}}\right]]

은닉층에 들어간 입력 벡터는 다음의 함수를 거쳐 출력층에 들어가는 벡터 $\mathbf{y}_{w_t}$ 가 됩니다.

[\mathbf{y}_{w_t} = b + W\mathbf{x} + U\cdot\tanh(d+H\mathbf{x})]

$W$ 는 단어 벡터 자체에 부여되는 가중치 행렬이고 $H$ 는 은닉층에서 단어 벡터에 가해지는 가중치입니다. 위 식에서 출력층에 들어가는 벡터를 생성하는 함수에서 2개의 가중치 행렬 $W, H$ 이 있는 이유는 임베딩 벡터, 즉 참조 테이블 $C$ 와 확률 함수의 변수를 동시에 학습하기 때문입니다. 위에서 본 그림을 다시 가져와보면 가장 왼쪽에 단어 벡터가 바로 출력층으로 바로 들어가는 경로(점선)가 있고, 은닉층을 거쳐 들어가는 경로(실선)가 있는 것을 알 수 있습니다.

이미지 출처 : imgur.com

출력층에서 계산되는 타겟 단어의 확률 $P$ 는 소프트맥스 함수에 의해서 구해집니다. 수식으로 나타내면 다음과 같습니다.

학습 이후

확률론적 신경망 언어 모델을 포함한 이후의 언어 모델은 위에서 말했던 것과 같이 단어의 의미 관계를 학습하기 때문에 말뭉치에 등장하지 않는 단어라도 생성해낼 수 있다는 장점이 있습니다. 단순한 예시로 다음과 같은 세 문장이 있는 말뭉치가 있다고 해봅시다.

“there are three teams left for qualification.” , “four teams have passed the first round.”, “four groups are playing in the field.”

신경망 언어 모델은 단어의 관계를 파악하기 때문에 말뭉치에는 없는 “three groups” 라는 단어 시퀀스를 만들어 낼 수 있게 됩니다.

확률론적 신경망 언어 모델은 2003년에 발표된 모델으로서 이후 등장하는 다양한 임베딩 방법보다는 성능이 좋지 않습니다. 하지만 임베딩을 통해 단어의 의미 관계를 보존하는 방식을 제안했다는 점에서 의의가 적지 않습니다.

본 포스트의 내용은 조경현 교수님의 강의 , 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 , 자연어 처리 인 액션 , 딥 러닝을 이용한 자연어 처리 입문 책을 참고하였습니다.

Language Model

이번 시간에 알아볼 N-gram(엔그램) 은 언어 모델(Language Models, LM) 에서 사용되는 횟수 기반의 벡터 표현방식(Count-based representation) 입니다. N-gram을 알아보기 전에 먼저 언어 모델이 무엇인지에 대해 간략하게 알아보도록 합시다.

언어 모델이란 무엇일까요? 언어 모델의 입력과 출력값을 보며 어떤 것을 수행하고자 하는 지를 유추해봅시다. 언어 모델에 입력되는 것은 하나의 문장이고, 출력값은 입력했던 문장에 대한 확률입니다. 이 확률은 입력은 문장이 얼마나 그럴듯한 지를 계산한 값입니다. 즉, 언어 모델의 목적은 가장 자연스러운 단어의 시퀀스를 찾아내는 것입니다. 수식으로 나타내면 다음과 같습니다.

[P(X) = P(x_1, x_2, \cdots, x_T)]

언어 모델은 말뭉치 내에 있는 수많은 단어 중 가장 적절한 결합을 찾아내기 위한 작업이므로 비지도 학습(Unsupervised Learning) 입니다. 하지만 비지도 학습은 어려우며 기법도 많이 나와있지 않습니다. 그렇기 때문에 단어(토큰)에 순서를 부여하여 연속되는 지도 학습(Supervised Learning)으로 바꾸어주기로 합니다.

Autoregressive Language Model

어떻게 지도학습으로 바꿀 수 있을까요? 자기회귀 언어모델(Autoregressive language model)이라는 방법을 사용합니다. 자기회귀 모델을 사용하면 다음에 올 토큰의 분포를 이전 모든 토큰들의 조건부 확률로 표현합니다. 그리고 이 방법을 문장이 끝나는 토큰 end of sentence 이 올 때까지 반복하면 하나의 문장이 완성되는 방식입니다. 자기회귀 언어모델을 사용하여 언어모델의 식을 변형해봅시다.

[\begin{aligned} P(X) &= P(x_1, x_2, \cdots, x_T)
&= P(x_1)P(x_2\vert x_1)P(x_3\vert x_1, x_2) … P(x_T\vert x_1, x_2 … x_{T-1})
&\because P(a,b) = P(a)P(b \vert a) \end{aligned}]

가장 아래 식을 풀어 설명해봅시다. 첫 번째 항인 $P(x_1)$ 은 단어 $x_1$ 이 문장의 첫 번째 자리로 올 확률입니다. 두 번째 항인 $P(x_2\vert x_1)$ 은 무엇일까요? 문장의 첫 번째 단어가 $x_1$ 일 때, 그 뒤에 $x_2$ 가 위치할 확률이 됩니다. 이렇게 문장이 끝나는 토큰이 올 때까지 구하는 것을 자기회귀 언어모델이라고 합니다.

자기회귀 언어모델의 하나마다의 입력과 출력은 어떻게 될까요? 이제는 문장 전체가 아니라 목표하는 토큰인 $x_T$ 이전까지의 모든 토큰의 시퀀스 $x_1, x_2 … x_{T-1}$ 를 입력합니다. 출력값은 $x_T$ 자리에 올 가능성이 있는 토큰들의 확률 분포가 됩니다.

하나의 예시를 들어봅시다. 자기회귀 언어모델은 “In Korea, more than half of residents speak Korean.” 이라는 문장을 어떻게 생성하게 될까요? 일단은 “In” 이 문장 맨 앞에 오는 것이 적절한지에 대한 확률(Scoring)을 계산합니다. 그 다음에는 “Korea” 가 “In” 뒤에 오는 것이 적절한지에 대한 확률을 계산합니다. 이 과정을 모든 단어에 대하여 반복합니다. 마지막 “Korean” 에 대한 확률은 “Korean” 이 “In Korea, more than half of residents speak” 뒤에 오는 것이 적절한가? 라는 질문에 대한 답이 됩니다. 예를 들어, “In Korea, more than half of residents speak Korean.” 와 “In Korea, more than half of residents speak Finnish.” 라는 선택지에서 전자의 확률이 더 높다고 판단하는 것이지요.

각 경우의 조건부 확률은 말뭉치에 등장하는 단어 시퀀스의 횟수를 통해 계산됩니다. 횟수의 통계로부터 계산하기 때문에 이 방법을 이후에 등장하는 신경망 기반의 언어모델과 구분하여 통계 기반의 언어 모델(Statistical Language Models) 이라고도 합니다. 예를 들어, 말뭉치에 “In Korea, more” 이라는 단어 시퀀스가 1000번 등장하였고 “In Korea, more than” 이 라는 단어 시퀀스가 600번 등장하였다면 조건부 확률 $P(\text{than} \vert\text{In Korea, more})$ 은 다음과 같이 계산됩니다.

[P(\text{than} \vert\text{In Korea, more}) = \frac{P(\text{In Korea, more than})}{P(\text{In Korea, more})} = \frac{600}{1000} = 0.6]

Sparsity

자기회귀 모델은 비지도 학습을 지도 학습으로 변화시켜 주지면 한 가지 문제를 가지고 있습니다. 가장 큰 문제는 데이터의 희소성(Sparsity)에 대한 문제입니다. 만약 말뭉치에 “In Korea, more than half of” 란 표현은 $k$ 번 등장하지만, “In Korea, more than half of residents” 란 표현은 한 번도 등장하지 않는다면 어떻게 될까요? “In Korea, more than half of residents speak Korean.” 라는 문장이 등장할 확률은 0이 됩니다. 수식으로 알아보도록 합시다.

[P(\text{residents} \vert \text{In Korea, more than half of}) = \frac{P(\text{In Korea, more than half of residents})}{P(\text{In Korea, more than half of})} = \frac{0}{k} = 0]

“In Korea, more than half of residents speak Korean.” 은 현실에서 사용 가능한 자연스러운 문장입니다. 하지만 말뭉치에 등장하지 않았다는 이유만으로 언어 모델은 이 문장을 생성할 수 없게 됩니다. 물론 말뭉치의 크기를 키우면 이런 문제가 줄어들기는 하지만 원천적으로 문제를 해결하기 위한 방법은 아닙니다. 이런 문제를 크게 개선하기 위해 나온 방법이 바로 N-gram 입니다.

N-gram

N-gram(엔그램) 은 Bag of Words , TF-IDF 와 같이 횟수를 사용하여 단어를 벡터로 표현(Count-based representation) 하는 방법입니다. 이전 두 방법을 사용할 때에는 한 개의 단어만을 분석 대상으로 삼았지만 N-gram은 한 단어 이상의 단어 시퀀스를 분석 대상으로 삼습니다. N-gram 앞에 N에 따라서 단어 시퀀스를 몇 개의 단어로 구성할 지를 결정하게 됩니다. $N = 1, 2, 3$ 인 경우를 각각 Uni-gram, Bi-gram, Tri-gram 이라 부르며 $N >= 4$ 일 때는 그냥 4-gram, 5-gram 의 방식으로 부릅니다. 아래의 그림을 통해 Uni-gram, Bi-gram, Tri-gram에서 단어 시퀀스가 어떻게 구성되는 지를 알아봅시다.

이미지 출처 : deepai.org

각각의 방법으로 $i$ 번째 토큰인 $x_i$ 의 조건부 확률을 구하면 다음과 같습니다.

[\begin{aligned} \text{Uni-gram : } P(x_i|x_1, x_2, \cdots , x_{i-1}) &\approx P(x_i)
\text{Bi-gram : } P(x_i|x_1, x_2, \cdots , x_{i-1}) &\approx P(x_i|x_{i-1})
\text{Tri-gram : } P(x_i|x_1, x_2, \cdots , x_{i-1}) &\approx P(x_i|x_{i-2}, x_{i-1}) \end{aligned}]

위와 같이 식을 변형할 수 있는 이유는 마르코프 가정(Markov assumption) 덕분입니다. 마르코프 가정이란 특정 시점에서 어떤 상태의 확률은 최근 상태에만 의존한다는 가정입니다. 즉, $x_i$ 의 확률을 그 이전에 있는 수 개의 토큰으로부터 추론할 수 있다는 것이지요. 수식으로 나타내면 다음과 같고 그 아래는 마르코프 가정을 사용한 마르코프 체인을 이미지로 나타낸 것입니다.

이미지 출처 : machlearnwiki

총 $T$ 개의 토큰으로 구성된 문장의 확률을 N-gram을 사용하여 나타내면 다음과 같이 됩니다.

[\begin{aligned} P(x_1, x_2, \cdots , x_T) &\approx \prod^T_{i=1} P(x_i|x_{i-k}, \cdots , x_{i-1}) \quad \text{[N-gram]}, N=k+1
&\approx \prod^T_{i=1} P(x_i) \quad \text{[Uni-gram]}
&\approx \prod^T_{i=1} P(x_i|x_{i-1}) \quad \text{[Bi-gram]}
&\approx \prod^T_{i=1} P(x_i|x_{i-1},x_{i-2}) \quad \text{[Tri-gram]} \end{aligned}]

N-gram이 어떻게 희소성 문제를 해결하는지 알아봅시다. 이전에 들었던 예시를 그대로 가져와 봅시다. 말뭉치에 “In Korea, more than half of” 라는 표현은 등장하지만 “In Korea, more than half of residents” 란 표현은 한 번도 등장하지 않는 경우를 가정하였습니다. N-gram은 문장의 처음부터 조건을 걸어주지 않아도 되기 때문에 조건이 매우 간단해집니다.

예를 들어, Bi-gram을 사용할 때 “of residents” 라는 단어가 한 번 이상 말뭉치에 등장한다면 “In Korea, more than half of” 의 뒤에 “residents” 라는 토큰이 올 확률은 0이 아니게 됩니다. 전체 문장인 “In Korea, more than half of residents speak Korean.” 의 확률을 구할 때도 “In Korea”, “Korea, more”, “more than”, … , “speak Korean.” 의 횟수만 세어가며 구하게 되지요. 하지만 N-gram도 여러 문제를 가지고 있습니다. 어떤 문제를 발생시킬까요?

Problems of N-grams

N-gram의 첫 번째 문제는 장기 의존성(Long-term dependency) 의 부재입니다. 이전에는 목표 토큰 이전에 있는 모든 토큰을 고려하여 목표 토큰의 확률을 계산하였습니다. 하지만 N-gram에서는 일부 단어 시퀀스의 횟수만을 가지고 판단하기 때문에 문장 앞쪽의 문맥을 고려하지 않은 채 토큰을 선택하게 됩니다.

위에서 사용했던 다른 예시를 다시 가져와 봅시다. “In Korea, more than half of residents speak Korean.” 와 “In Korea, more than half of residents speak Finnish.” 중 더 적절한 문장을 고르는 문제입니다. 마지막 단어 토큰을 선택할 때 이전에 위치한 모든 토큰을 고려한다면 당연히 “In Korea, more than half of residents speak Korean.” 를 선택할 것입니다. 말뭉치에 “In Korea, more than half of residents speak Korean.” 가 등장할 확률이 “In Korea, more than half of residents speak Finnish.” 가 등장할 확률보다는 높겠지요.

하지만 N-gram을 사용하면 어떻게 될까요? 다시 Bi-gram을 사용하는 경우를 생각해봅시다. 우리가 준비한 말뭉치에 “speak Finnish.” 라는 시퀀스가 “speak Korean.” 보다 많이 등장할 수 있습니다. 이렇게 된다면 충분히 “In Korea, more than half of residents speak Finnish.” 라는 사실과 다른 문장을 컴퓨터가 만들 수 있게 됩니다.

실제로 N-gram을 사용할 때는 $N=1 \sim 5$ 까지 여러 N-gram을 섞어 사용하여 이런 문제를 해결합니다. 의존성 분석(Dependency parsing)도 장기 의존성 문제를 해결하기 위한 방법입니다. 의존성 분석의 방법에는 Shift reduce parsing 과 같은 Transition-based Model과 토큰끼리의 의존성 구조를 그래프로 표현한 Graph-based Model이 있습니다.

이미지 출처 : researchgate.net

그런데 $N$ 을 $7,8$ 정도로 늘리면 장기 의존성 문제가 해결되지 않을까요? 그런데 왜 N을 증가시키지 않는 것일까요? $N$ 을 증가시키면 이전에 살펴보았던 희소성 문제가 부활하게 됩니다. 실제로 $N >= 7$ 인 N-gram에서는 대부분의 시퀀스 등장 확률이 0이 됩니다. 그리고 Bi-gram과 같이 짧은 단어 시퀀스에서도 희소성(Sparsity) 문제는 여전히 발생합니다.

예를 들어, “마라룽샤를 요리하다.” 라는 단어는 실제로 사용할 수 있는 단어이지만 실제로 많이 쓰는 단어는 아니기 때문에 우리가 학습에 사용할 말뭉치에 없을 수도 있습니다. “마라룽샤를 요리하다” 는 “컵을 요리하다”, “책꽂이를 요리하다” 와 달리 자연스러운 문장임에도 등장 확률은 0이 됩니다. N-gram 모델에서 발생하는 희소성 문제를 해결하기 위해서 스무딩(Smoothing) 과 백오프(Backoff) 라는 방법이 사용되고 있습니다.

스무딩은 발생 횟수가 0이 되지 않도록 단어 시퀀스의 출현 빈도를 보정해주는 방법입니다. 가장 기본적인 스무딩으로는 모든 단어 시퀀스의 출현 빈도에 작은 값을 더해주는 방법이 있습니다. 아래는 모든 단어 시퀀스의 출현 횟수에 $k$ 를 더해주는 스무딩을 수식으로 나타낸 것입니다.

백오프는 $p=0$ 이 되는 경우에만 $N$ 을 더 작게하는 방법입니다. 예를 들어, Bi-gram을 사용하면서 “마라룽샤를 요리하다” 가 없을 경우에는 Uni-gram을 사용하여 “마라룽샤를” 을 찾습니다. 백오프를 사용할 경우에는 보정을 위해서 Correction factor $\alpha, \beta$ 를 사용해줍니다. 수식으로 표현하면 아래와 같습니다.

[c(x_{-N}, … ,x) = \begin{cases}{\alpha}c(x_{-N+1}, … ,x) + \beta \quad \text{if } c(x_{-N}, … ,x) = 0 \ c(x_{-N}, … ,x) \qquad \qquad \text{ otherwise} \end{cases}]

가장 널리 사용되는 방법으로는 Kneser-Ney(KN) 스무딩 방법이 있습니다. 기본적인 아이디어는 목적이 되는 단어 $w$ 이전에 나타나는 단어 $v$ 가 얼마나 다양한 지를 알아내는 데에 있습니다. $v$ 가 클수록 말뭉치에서 나타나지 않는 단어 시퀀스가 될 가능성이 높기 때문입니다. KN 스무딩은 다음의 수식을 사용하여 단어가 나타날 확률 $P_{KN}$ 을 나타냅니다.

[P_{KN} (w_i|w_{i-1}) = \frac{\max(\text{Count}(w_{i-1},w_i) - d,0)}{\text{Count}(w_i)} + \lambda(w_{i-1}) \times \text{Score}{\text{continuation}}(w_i)
\begin{aligned} \text{where} \quad &\lambda(w{i-1}) = \frac{d}{\sum_v \text{Count}(w_{i-1})} \times |{w:c(w_{i-1},v) > 0}|
&\text{Score}{\text{continuation}}(w_i) = \frac{|{v:\text{Count}(v,w) > 0}|}{\sum{w^{\prime}}|{v:\text{Count}(v,w^{\prime}) > 0}|} \end{aligned}]

위 식에서 $d$ 는 하이퍼파라미터이며 일반적으로는 0.75를 사용합니다. 또한 Score를 산출하는 식에서 $w^\prime$ 은 $v$ 뒤에 등장하는 다른 단어를 나타냅니다. KN 스무딩은 KenLM 패키지 내에 구현되어 있습니다.