재귀와 병합 정렬(Recursion & Merge Sort)
29 Jun 2020 | Data Structure
본 게시물은 문일철 교수님의 데이터 구조 및 분석을 참조하여 작성하였습니다.
Recursions
Divide & Conquer

이미지 출처 : wikipedia : Fractal
어떤 문제들은 위 그림에서 볼 수 있는 것처럼 작게 나누더라도 동일한 구조를 가지는 경우가 있습니다. 예를 들어, 그림과 같은 조직도를 가진 회사에서 예산을 나누는 경우를 생각해보겠습니다.

이미지 출처 : swuc21.com
정해진 총 예산을 $\mathbf{N}$ 이라 합시다. 이를 Sales, Manufacturing, Customer Support에 $N_1, N_2, N_3$ 로 나눠 배정하게 됩니다. 그리고 Manufacturing 내에 있는 Department는 $N_2$ 를 또 다시 부서 내부의 각 팀에 $n_1, n_2,n_3$ 만큼 배정합니다.
이렇게 어떤 문제는 더 작게 나누더라도 구조적으로는 동일한 문제가 반복됩니다. 이렇게 문제를 나누어 생각해도 동일한 구조를 가지는(Self-similar) 문제를 Repeating Problem 이라고 합니다. 이 때 문제를 작게 나누는 행위를 분할(Divide) , 그리고 나눈 문제를 해결하는 것을 정복(Conquer) 이라고 합니다. 마치 아래의 마트료시카 인형처럼 큰 문제를 계속 작게 분할해나가고, 가장 작은 문제부터 정복해 올라오게 되지요.

이미지 출처 : dookinternational.com
이러한 Repeating Problem에 해당하는 문제는 어떤 것들이 있을까요? 대표적인 형태는 수학에서 점화식(Mathmatical Induction)으로 나타나는 것들입니다. 가장 대표적인 예시로 팩토리얼(Factorial)을 구하는 과정이 이에 해당합니다. 팩토리얼을 구하는 과정을 수식으로 나타내면 아래와 같습니다.
[\text{Factorial}(n) = \begin{cases} 1 \qquad \qquad \qquad \qquad \qquad \text{if} \quad n = 0\ n \times n-1 \times \cdots \times 2 \times 1 \quad \text{if} \quad n > 0 \end{cases}
\text{Factorial}(n) = \begin{cases} 1 \qquad \qquad \qquad \qquad \qquad \text{if} \quad n = 0\ n \times\text{Factorial}(n-1) \qquad \text{if} \quad n > 0 \end{cases}]
Recursion
위와 같이 Repeating problem을 분할과 정복을 사용하여 푸는 가장 일반적인 방법이 바로 재귀(Recursion)입니다. 재귀의 코드는 일반적으로 다음과 같은 형태를 띠고 있습니다.
def recursionFunction(target):
if escapeCondition: # 탈출을 위한 조건문
return Value
# ... 함수 내용
recursionFunction(target_) # 재귀 호출
재귀 함수에는 두 가지의 필수적인 요소가 있습니다. 하나는 탈출을 위한 조건문입니다. 이 조건문이 있어야 분할한 문제를 하나씩 정복하여 원하는 값을 얻을 수 있습니다. 두 번째는 다시 자신을 호출하는 함수 호출문입니다. 대신 함수 안에서 호출되는 함수의 인자는 원래 함수의 인자를 축소한 것이어야 합니다. 더 작은 문제로 나아가기 위함입니다.
글로만 이해하기는 어려우니 예시 코드를 보겠습니다. 아래는 재귀 문제의 대표적인 예시인 피보나치 수열을 파이썬 코드로 구현한 것입니다.
def Fibonacci(n):
if n == 0:
return 0
if n == 1:
return 1
intRet = Fibonacci(n-1) + Fibonacci(n-2)
return intRet
함수 코드의 상단에는 각 상황에서의 탈출문이 구현되어 있는 것을 볼 수 있습니다. 그 아래에는 더 작은 인자를 가지는 피보나치 함수를 다시 호출하고 있는 것을 볼 수 있습니다. 임의의 인자를 넣어 이 재귀 함수의 인자가 어떻게 작동하는 지 보도록 하겠습니다. $n=5$, 즉 Fibonacci(5) 일 때 이 함수가 호출되는 과정을 그림으로 나타내면 아래와 같이 됩니다.

이미지 출처 : andreagrandi.it
가장 먼저 $fib(5)$ 로부터 $fib(4), fib(3)$ 이 호출됩니다. 이 중에서 $fib(4)$가 있는 왼쪽을 먼저 보겠습니다. $fib(4)$는 다시 $fib(3)$과 $fib(2)$를 호출합니다. 여기서 $fib(4)$ 왼쪽 아래의 $fib(3)$ 이하의 형태와 $fib(5)$ 오른쪽 아래의 $fib(3)$ 이하의 형태가 동일한 것을 볼 수 있습니다. $fib(4)$ 오른쪽 아래의 $fib(2)$ 이하의 형태와 $fib(3)$ 왼쪽 아래의 $fib(2)$ 이하의 형태 역시 동일한 것도 볼 수 있지요. 이렇게 동일한 형태가 계속 반복되면서 호출 그래프의 맨 아래에는 $fib(1)$과 $fib(0)$만 남게 됩니다.
이 $fib(1)$과 $fib(0)$은 탈출 조건문에 의해 값을 구할 수 있습니다. 이 값으로부터 $fib(2),fib(3),fib(4),fib(5)$의 값을 차례대로 구해나가게 됩니다.
in Stackframe
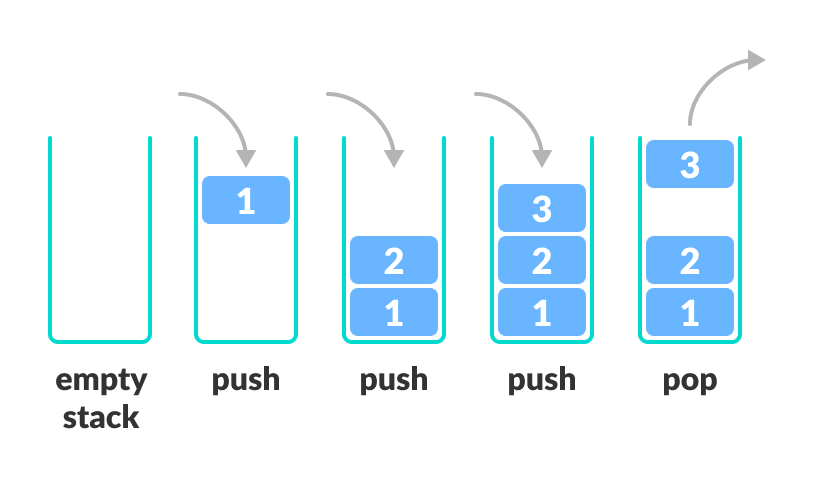
이렇게 재귀 함수를 호출하면 컴퓨터 안에서는 어떤 일이 일어나는지 알아보겠습니다. 재귀 함수가 호출되면 컴퓨터는 스택 프레임(Stack frame) 내부에 함수 호출 아이템(Item)을 쌓아갑니다. 스택 프래임이란 함수 호출 이력을 저장하는 스택이며 쌓이는 아이템은 함수 내에 있는 지역 변수와 함수 호출 인자가 포함되어 있습니다. 함수가 호출되면 아이템이 push 되고, 함수가 끝나거나 리턴되면 호출 요청되면 아이템이 pop 됩니다.
아래는 재귀로 구현한 피보나치 함수를 호출했을 때 스택 프레임 $fib(5)$ 는 너무 복잡하므로 한 단계 낮은 인자인 $fib(4)$를 컴퓨터가 어떻게 처리하는 지에 대한 그림입니다.

이미지 출처 : knowledge-cess.com
위 그림을 보면 가장 먼저 호출된 $fib(4)$ 가 push 됩니다. 그 위로 $fib(3), fib(2)$ 가 호출되어 push 되고 있는 것을 볼 수 있습니다. 계속해서 이렇게 호출된 함수들이 분할한 함수 호출을 계속해서 쌓아나갑니다. 이렇게 호출된 모든 함수가 스택 프레임에 쌓이게 되면 맨 위쪽부터 pop 이 되며 빠져나갑니다. 아이템이 차례대로 pop 되면 스택 프레임의 맨 아래에서 처음에 호출했던 $fib(4)$의 값을 구할 수 있게 됩니다.
Merge Sort
병합 정렬(Merge sort)은 다양한 정렬 중에서 재귀를 이용합 정렬 방법을 사용합니다. 병합 정렬은 분할에 해당하는 분해(Decomposition)와 정복에 해당하는 통합(Aggregation)으로 이루어져 있는 분할-정복 알고리즘 중 하나입니다. 분해는 하나의 리스트를 반씩 토막내는 메커니즘이고 통합은 2개의 리스트의 요소를 작은 순서대로 하나의 리스트로 합쳐 배열하는 메커니즘입니다.

이미지 출처 : wikipedia.org
병합 정렬을 파이썬 코드로 구현하면 다음과 같이 쓸 수 있다.
import random
def performMergeSort(lstElementToSort):
# 탈출을 위한 조건문
if len(lstElementToSort) == 1:
return lstElementToSort
"""
Decomposition
1개를 길이가 같은 2개의 리스트로 분리한다
"""
lstSubElementToSort1 = []
lstSubElementToSort2 = []
for itr in range(len(lstElementToSort)):
if len(lstElementToSort)/2 > itr:
lstElementToSort1.append(lstElementToSort[itr])
else:
lstElementToSort2.append(lstElementToSort[itr])
"""
Recursion
리스트의 원소가 1개가 될 때까지 분리 과정을 반복한다
"""
lstSubElementToSort1 = performMergeSort(lstSubElementToSort1)
lstSubElementToSort2 = performMergeSort(lstSubElementToSort2)
"""
Aggregation
각 리스트 앞부분 부터 요소의 크기를 순차적으로 비교한 뒤
크기가 작은 것부터 새로운 리스트의 앞부분에 배치한다
"""
idxCount1 = 0
idxCount2 = 0
for itr in range(len(lstElementToSort)):
if idxCount1 == len(lstSubElementToSort1):
lstElementToSort[itr] = lstSubElementToSort2[idxCount2]
idxCount2 += 1
elif idxCount2 == len(lstSubElementToSort2):
lstElementToSort[itr] = lstSubElementToSort1[idxCount1]
idxCount1 += 1
elif lstSubElementToSort1[idxCount1] > lstSubElementToSort2[idxCount2]:
lstElementToSort[itr] = lstSubElementToSort2[idxCount2]
idxCount2 += 1
else:
lstElementToSort[itr] = lstSubElementToSort1[idxCount1]
idxCount1 += 1
return lstElementToSort
Problems
재귀 호출에도 문제점이 있습니다. 재귀 호출의 문제점을 단적으로 보여줄 수 있는 사례가 바로 피보나치 수열입니다. 위에서 보았던 피보나치 함수의 호출 그래프를 다시 가져와 보겠습니다.

이미지 출처 : andreagrandi.it
이어서 피보나치 함수의 인자를 5에서 7로 늘리면 어떻게 되는 지도 보겠습니다.

이미지 출처 : semanticscholar.org
인자가 5에서 7로만 늘어났는데도 함수 호출 그래프가 엄청나게 복잡해진 것을 볼 수 있습니다. 만약 $fib(10), fib(20)$ 정도를 호출한다면 지면이 허용하지 않을 정도로 함수 그래프가 복잡해질 것입니다. 함수 그래프가 이렇게 복잡해지는 이유는 무엇일까요? 바로 탈출문이 나올 때까지 분할 과정을 계속하기 때문입니다. 위 그림에서도 $fib(0), fib(1)$이 나올 때까지 모두 분할하기 때문에 $fib(0)$은 8번, $fib(1)$은 무려 13번이나 호출되고 있습니다.
이 때문에 재귀를 사용했을 때 걸리는 시간은 $N$이 일정 수준 이상으로 커지면 기하급수적으로 늘어나게 됩니다. 아래는 재귀로 구현된 피보나치 함수를 사용했을 때 걸리는 시간을 그래프로 나타낸 것입니다. $N \geq 30$ 일 때는 엄청나게 많은 시간이 걸리는 것을 볼 수 있지요.

이미지 출처 : proc-x.com
이런 문제를 어떻게 해결할 수 있을까요? 재귀의 문제는 모든 함수를 탈출문이 나올 때까지 쪼갠다는 것이었습니다. 끝까지 쪼개지 않고 $fib(2)$를 한 번 구한다면 분할 없이 그 값을 바로 가져오고, $fib(3)$도 값을 알고난 후에는 분할 없이 그 값을 그대로 가져올 수 있다면 훨씬 빠르게 원하는 값을 구할 수 있을 것입니다. $fib(2), fib(3), \cdots$ 등의 값을 구하여 어디엔가 저장해 놓고 가져오기만 하는 것이지요.
이런 방식을 사용하여 재귀의 함수 호출 문제를 풀어낼 수 있습니다. 이것이 바로 다음에 등장할 동적 프로그래밍(Dynamic programming)입니다.
본 게시물은 문일철 교수님의 데이터 구조 및 분석을 참조하여 작성하였습니다.
Recursions
Divide & Conquer

이미지 출처 : wikipedia : Fractal
어떤 문제들은 위 그림에서 볼 수 있는 것처럼 작게 나누더라도 동일한 구조를 가지는 경우가 있습니다. 예를 들어, 그림과 같은 조직도를 가진 회사에서 예산을 나누는 경우를 생각해보겠습니다.

이미지 출처 : swuc21.com
정해진 총 예산을 $\mathbf{N}$ 이라 합시다. 이를 Sales, Manufacturing, Customer Support에 $N_1, N_2, N_3$ 로 나눠 배정하게 됩니다. 그리고 Manufacturing 내에 있는 Department는 $N_2$ 를 또 다시 부서 내부의 각 팀에 $n_1, n_2,n_3$ 만큼 배정합니다.
이렇게 어떤 문제는 더 작게 나누더라도 구조적으로는 동일한 문제가 반복됩니다. 이렇게 문제를 나누어 생각해도 동일한 구조를 가지는(Self-similar) 문제를 Repeating Problem 이라고 합니다. 이 때 문제를 작게 나누는 행위를 분할(Divide) , 그리고 나눈 문제를 해결하는 것을 정복(Conquer) 이라고 합니다. 마치 아래의 마트료시카 인형처럼 큰 문제를 계속 작게 분할해나가고, 가장 작은 문제부터 정복해 올라오게 되지요.

이미지 출처 : dookinternational.com
이러한 Repeating Problem에 해당하는 문제는 어떤 것들이 있을까요? 대표적인 형태는 수학에서 점화식(Mathmatical Induction)으로 나타나는 것들입니다. 가장 대표적인 예시로 팩토리얼(Factorial)을 구하는 과정이 이에 해당합니다. 팩토리얼을 구하는 과정을 수식으로 나타내면 아래와 같습니다.
[\text{Factorial}(n) = \begin{cases} 1 \qquad \qquad \qquad \qquad \qquad \text{if} \quad n = 0\ n \times n-1 \times \cdots \times 2 \times 1 \quad \text{if} \quad n > 0 \end{cases}
\text{Factorial}(n) = \begin{cases} 1 \qquad \qquad \qquad \qquad \qquad \text{if} \quad n = 0\ n \times\text{Factorial}(n-1) \qquad \text{if} \quad n > 0 \end{cases}]
Recursion
위와 같이 Repeating problem을 분할과 정복을 사용하여 푸는 가장 일반적인 방법이 바로 재귀(Recursion)입니다. 재귀의 코드는 일반적으로 다음과 같은 형태를 띠고 있습니다.
def recursionFunction(target):
if escapeCondition: # 탈출을 위한 조건문
return Value
# ... 함수 내용
recursionFunction(target_) # 재귀 호출
재귀 함수에는 두 가지의 필수적인 요소가 있습니다. 하나는 탈출을 위한 조건문입니다. 이 조건문이 있어야 분할한 문제를 하나씩 정복하여 원하는 값을 얻을 수 있습니다. 두 번째는 다시 자신을 호출하는 함수 호출문입니다. 대신 함수 안에서 호출되는 함수의 인자는 원래 함수의 인자를 축소한 것이어야 합니다. 더 작은 문제로 나아가기 위함입니다.
글로만 이해하기는 어려우니 예시 코드를 보겠습니다. 아래는 재귀 문제의 대표적인 예시인 피보나치 수열을 파이썬 코드로 구현한 것입니다.
def Fibonacci(n):
if n == 0:
return 0
if n == 1:
return 1
intRet = Fibonacci(n-1) + Fibonacci(n-2)
return intRet
함수 코드의 상단에는 각 상황에서의 탈출문이 구현되어 있는 것을 볼 수 있습니다. 그 아래에는 더 작은 인자를 가지는 피보나치 함수를 다시 호출하고 있는 것을 볼 수 있습니다. 임의의 인자를 넣어 이 재귀 함수의 인자가 어떻게 작동하는 지 보도록 하겠습니다. $n=5$, 즉 Fibonacci(5) 일 때 이 함수가 호출되는 과정을 그림으로 나타내면 아래와 같이 됩니다.

이미지 출처 : andreagrandi.it
가장 먼저 $fib(5)$ 로부터 $fib(4), fib(3)$ 이 호출됩니다. 이 중에서 $fib(4)$가 있는 왼쪽을 먼저 보겠습니다. $fib(4)$는 다시 $fib(3)$과 $fib(2)$를 호출합니다. 여기서 $fib(4)$ 왼쪽 아래의 $fib(3)$ 이하의 형태와 $fib(5)$ 오른쪽 아래의 $fib(3)$ 이하의 형태가 동일한 것을 볼 수 있습니다. $fib(4)$ 오른쪽 아래의 $fib(2)$ 이하의 형태와 $fib(3)$ 왼쪽 아래의 $fib(2)$ 이하의 형태 역시 동일한 것도 볼 수 있지요. 이렇게 동일한 형태가 계속 반복되면서 호출 그래프의 맨 아래에는 $fib(1)$과 $fib(0)$만 남게 됩니다.
이 $fib(1)$과 $fib(0)$은 탈출 조건문에 의해 값을 구할 수 있습니다. 이 값으로부터 $fib(2),fib(3),fib(4),fib(5)$의 값을 차례대로 구해나가게 됩니다.
in Stackframe
이렇게 재귀 함수를 호출하면 컴퓨터 안에서는 어떤 일이 일어나는지 알아보겠습니다. 재귀 함수가 호출되면 컴퓨터는 스택 프레임(Stack frame) 내부에 함수 호출 아이템(Item)을 쌓아갑니다. 스택 프래임이란 함수 호출 이력을 저장하는 스택이며 쌓이는 아이템은 함수 내에 있는 지역 변수와 함수 호출 인자가 포함되어 있습니다. 함수가 호출되면 아이템이 push 되고, 함수가 끝나거나 리턴되면 호출 요청되면 아이템이 pop 됩니다.
아래는 재귀로 구현한 피보나치 함수를 호출했을 때 스택 프레임 $fib(5)$ 는 너무 복잡하므로 한 단계 낮은 인자인 $fib(4)$를 컴퓨터가 어떻게 처리하는 지에 대한 그림입니다.

이미지 출처 : knowledge-cess.com
위 그림을 보면 가장 먼저 호출된 $fib(4)$ 가 push 됩니다. 그 위로 $fib(3), fib(2)$ 가 호출되어 push 되고 있는 것을 볼 수 있습니다. 계속해서 이렇게 호출된 함수들이 분할한 함수 호출을 계속해서 쌓아나갑니다. 이렇게 호출된 모든 함수가 스택 프레임에 쌓이게 되면 맨 위쪽부터 pop 이 되며 빠져나갑니다. 아이템이 차례대로 pop 되면 스택 프레임의 맨 아래에서 처음에 호출했던 $fib(4)$의 값을 구할 수 있게 됩니다.
Merge Sort
병합 정렬(Merge sort)은 다양한 정렬 중에서 재귀를 이용합 정렬 방법을 사용합니다. 병합 정렬은 분할에 해당하는 분해(Decomposition)와 정복에 해당하는 통합(Aggregation)으로 이루어져 있는 분할-정복 알고리즘 중 하나입니다. 분해는 하나의 리스트를 반씩 토막내는 메커니즘이고 통합은 2개의 리스트의 요소를 작은 순서대로 하나의 리스트로 합쳐 배열하는 메커니즘입니다.

이미지 출처 : wikipedia.org
병합 정렬을 파이썬 코드로 구현하면 다음과 같이 쓸 수 있다.
import random
def performMergeSort(lstElementToSort):
# 탈출을 위한 조건문
if len(lstElementToSort) == 1:
return lstElementToSort
"""
Decomposition
1개를 길이가 같은 2개의 리스트로 분리한다
"""
lstSubElementToSort1 = []
lstSubElementToSort2 = []
for itr in range(len(lstElementToSort)):
if len(lstElementToSort)/2 > itr:
lstElementToSort1.append(lstElementToSort[itr])
else:
lstElementToSort2.append(lstElementToSort[itr])
"""
Recursion
리스트의 원소가 1개가 될 때까지 분리 과정을 반복한다
"""
lstSubElementToSort1 = performMergeSort(lstSubElementToSort1)
lstSubElementToSort2 = performMergeSort(lstSubElementToSort2)
"""
Aggregation
각 리스트 앞부분 부터 요소의 크기를 순차적으로 비교한 뒤
크기가 작은 것부터 새로운 리스트의 앞부분에 배치한다
"""
idxCount1 = 0
idxCount2 = 0
for itr in range(len(lstElementToSort)):
if idxCount1 == len(lstSubElementToSort1):
lstElementToSort[itr] = lstSubElementToSort2[idxCount2]
idxCount2 += 1
elif idxCount2 == len(lstSubElementToSort2):
lstElementToSort[itr] = lstSubElementToSort1[idxCount1]
idxCount1 += 1
elif lstSubElementToSort1[idxCount1] > lstSubElementToSort2[idxCount2]:
lstElementToSort[itr] = lstSubElementToSort2[idxCount2]
idxCount2 += 1
else:
lstElementToSort[itr] = lstSubElementToSort1[idxCount1]
idxCount1 += 1
return lstElementToSort
Problems
재귀 호출에도 문제점이 있습니다. 재귀 호출의 문제점을 단적으로 보여줄 수 있는 사례가 바로 피보나치 수열입니다. 위에서 보았던 피보나치 함수의 호출 그래프를 다시 가져와 보겠습니다.

이미지 출처 : andreagrandi.it
이어서 피보나치 함수의 인자를 5에서 7로 늘리면 어떻게 되는 지도 보겠습니다.

이미지 출처 : semanticscholar.org
인자가 5에서 7로만 늘어났는데도 함수 호출 그래프가 엄청나게 복잡해진 것을 볼 수 있습니다. 만약 $fib(10), fib(20)$ 정도를 호출한다면 지면이 허용하지 않을 정도로 함수 그래프가 복잡해질 것입니다. 함수 그래프가 이렇게 복잡해지는 이유는 무엇일까요? 바로 탈출문이 나올 때까지 분할 과정을 계속하기 때문입니다. 위 그림에서도 $fib(0), fib(1)$이 나올 때까지 모두 분할하기 때문에 $fib(0)$은 8번, $fib(1)$은 무려 13번이나 호출되고 있습니다.
이 때문에 재귀를 사용했을 때 걸리는 시간은 $N$이 일정 수준 이상으로 커지면 기하급수적으로 늘어나게 됩니다. 아래는 재귀로 구현된 피보나치 함수를 사용했을 때 걸리는 시간을 그래프로 나타낸 것입니다. $N \geq 30$ 일 때는 엄청나게 많은 시간이 걸리는 것을 볼 수 있지요.

이미지 출처 : proc-x.com
이런 문제를 어떻게 해결할 수 있을까요? 재귀의 문제는 모든 함수를 탈출문이 나올 때까지 쪼갠다는 것이었습니다. 끝까지 쪼개지 않고 $fib(2)$를 한 번 구한다면 분할 없이 그 값을 바로 가져오고, $fib(3)$도 값을 알고난 후에는 분할 없이 그 값을 그대로 가져올 수 있다면 훨씬 빠르게 원하는 값을 구할 수 있을 것입니다. $fib(2), fib(3), \cdots$ 등의 값을 구하여 어디엔가 저장해 놓고 가져오기만 하는 것이지요.
이런 방식을 사용하여 재귀의 함수 호출 문제를 풀어낼 수 있습니다. 이것이 바로 다음에 등장할 동적 프로그래밍(Dynamic programming)입니다.