ELMo (Embeddings from Language Models)
03 Jul 2020 | NLP
본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 책을 참고하였습니다.
ELMo

이미지 출처 : 트위터 - Elmo
ELMo(Embeddings from Language Models)는 2018년 6월에 “Deep contextualized word representations” 논문을 통해 발표된 임베딩 모델입니다. “Embeddings from Language Models”라는 말 그대로 언어 모델로부터 만들어진 임베딩이며 더 좋은 단어 표현(Representation)을 위해 만들어졌습니다.
논문에서는 좋은 단어 표현의 조건으로 두 가지를 제시하고 있습니다. 첫 번째는 단어의 구조(Syntax)적 특성과 의미(Semantic)적 특성을 모두 만족시키는 표현이어야 합니다. 두 번째는 언어학적으로 문맥에 맞는 표현을 할 수 있어야 합니다. 아래는 “stick”이라는 표현에 대한 임베딩을 ELMo에게 부탁하는 장면입니다.

이미지 출처 : http://jalammar.github.io
이전 모델에서는 “stick”이라는 단어를 보면 문맥상 의미는 배제한 채 말뭉치에서 학습한 대로 임베딩했습니다. 하지만 엘모는 단어만 가지고는 답을 주지 않습니다. 엘모는 그 단어가 쓰인 문장이 어떤 것이며 단어가 그 문장에서 어떤 구조나 의미를 가지고 있는지를 알아야 임베딩 벡터를 내놓게 됩니다.
ELMo(biLM)과 GloVe를 비교한 하나의 예시를 더 보겠습니다. 아래 그림에서는 각 임베딩 모델로부터 “play”와 비슷한 단어를 나타낸 결과입니다.

이미지 출처 : slideshare.net/shuntaroy
위 그림에서 GloVe로 임베딩하면 “play”라는 단어와 비슷한 단어를 뽑았을 때 “playing, game, games, players …” 등 스포츠와 관련된 단어들이 있는 것을 알 수 있습니다. 하지만 ELMo는 “play”가 문장에서 어떤 의미로 사용되었는 지를 구분합니다. 표에서 2행에 있는 “play”는 GloVe가 판단한 것과 동일한 “(스포츠)경기”를 의미하고 있으며 마지막 행에 있는 “(a Broadway) play”를 의미하고 있습니다. ELMo는 이를 문맥에 맞게 잘 판단하고 있는 것을 볼 수 있습니다.
bi-LSTM
ELMo는 문장을 입력받아 단어 토큰의 임베딩 벡터를 만듭니다. 이런 점에서 단어나 서브워드를 입력받았던 Word2Vec, GloVe, Fasttext 등의 이전 모델과 차이점을 갖습니다. 커다란 말뭉치를 2개 층으로 이루어진 bi-LSTM(bidirectional LSTM, 양방향 LSTM)이 만들어내는 임베딩 벡터를 사용합니다.
이 벡터는 bi-LSTM의 내부 층에 대한 은닉 벡터(Hidden vector)에 가중치를 부여한 뒤에 선형 결합(Linear combination)하여 사용합니다. 이렇게 선형 결합을 통해 나타나는 벡터는 단어가 가진 많은 특성에 대한 정보를 담고 있게 됩니다. 각 은닉 벡터 중에서 위쪽에 위치한 LSTM은 단어의 문맥적인(Context-dependent) 의미를 포착할 수 있고 아래쪽에 위치한 LSTM은 단어의 구조적인(Syntax) 의미를 포착할 수 있습니다.
따라서 단어의 구조적인 표현이 중요해지는 구문 분석(Syntax Analysis)이나 품사 태깅(POS Tagging) 등의 태스크에는 아래쪽 biLSTM층이 만들어 내는 은닉 벡터에 가중치를 더 많이 주게 됩니다. 반대로 의미적인 표현이 중요해지는 NLU(Natural Language Understanding)이나 QA(Question&Answering) 등의 태스크에는 위쪽 biLSTM층이 만들어 내는 은닉 벡터에 더 많은 가중치를 부여하게 되지요.
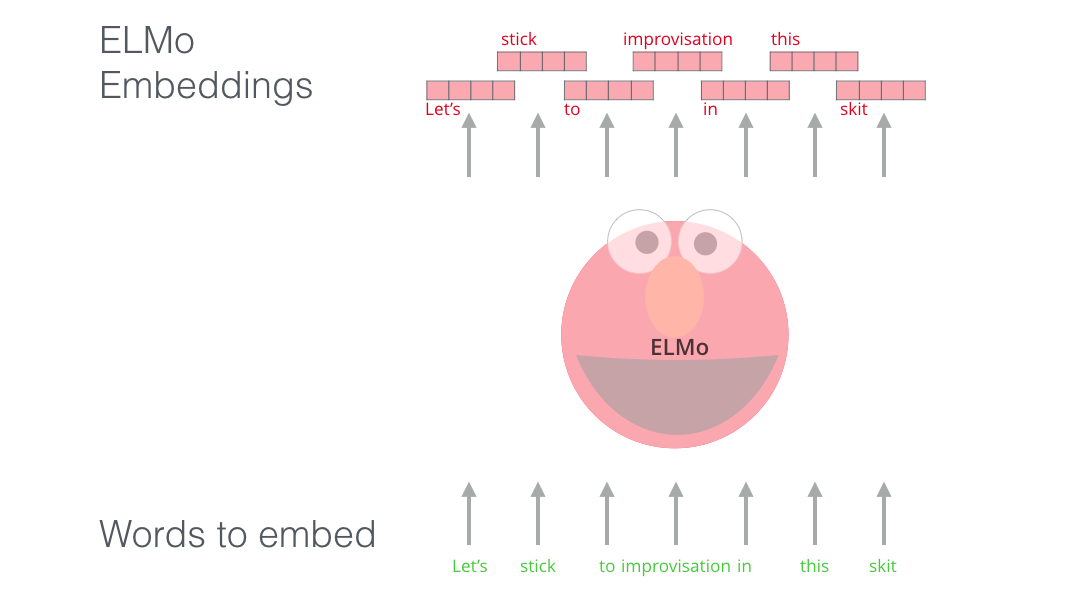
ELMo는 전체 문장을 본 후에 문장을 구성하는 단어에 임베딩을 해줍니다. 아래는 “Let’s stick to improvisation in this skit”이라는 문장을 입력했을 때 단어가 임베딩되는 과정을 도식화하여 보여주고 있습니다.
이미지 출처 : http://jalammar.github.io
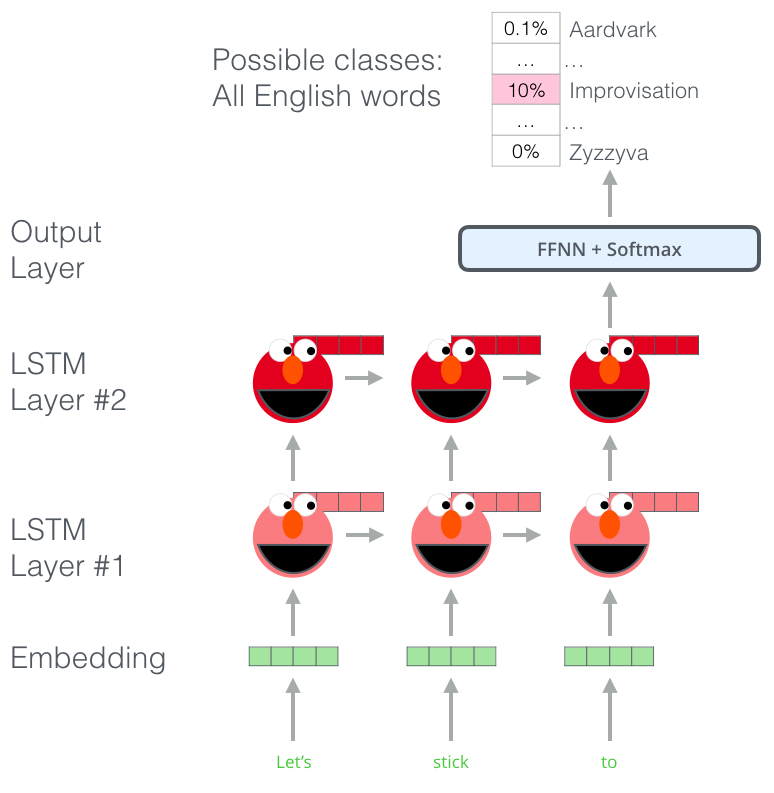
ELMo는 기본적으로 언어 모델(Language Models)을 따르고 있기 때문에 타겟 단어 이전까지의 시퀀스로부터 타겟 단어를 예측합니다. 아래는 “Let’s stick to improvisation in this skit”에서 ELMo가 “improvisation”을 예측하는 과정을 보여주는 이미지입니다. (엘모는 귀엽습니다)
이미지 출처 : http://jalammar.github.io
ELMo는 단방향으로의 LSTM이 아니라 biLSTM, 즉 양방향으로 진행하는 LSTM을 사용하여 학습합니다. 아래는 ELMo가 입력 문장을 양방향으로 읽어 나간다는 것을 도식화한 이미지입니다. (엘모는 보라색도 귀엽습니다)
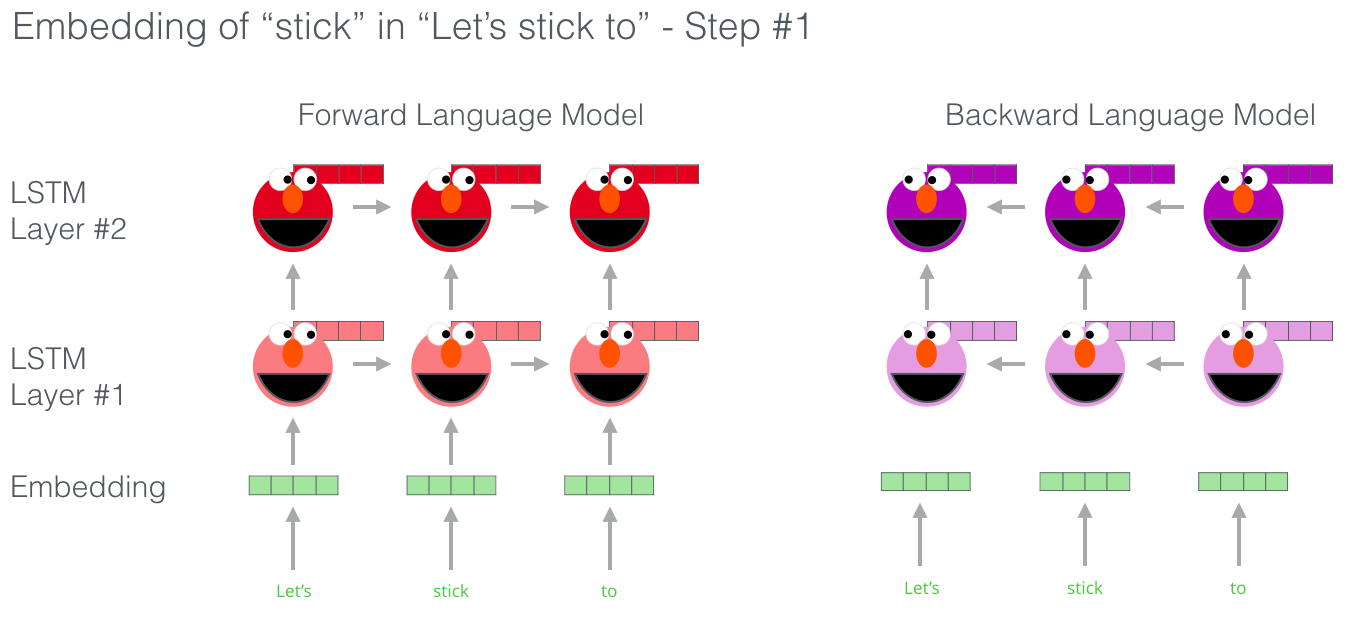
이미지 출처 : http://jalammar.github.io
이후에는 단어마다 순방향(Forward) LSTM의 은닉 벡터 및 토큰 임베딩 벡터와 역방향(Backward) LSTM의 은닉 벡터 및 토큰 임베딩 벡터를 Concatenate합니다. 그리고 이어붙인 벡터에 각각 가중치 $s_0, s_1, s_2$ 를 곱해줍니다. 마지막으로 세 벡터를 더해준 벡터를 ELMo 임베딩 벡터로 사용합니다. 아래는 이 “stick”이라는 단어가 ELMo 임베딩 되는 과정을 보여주고 있습니다.
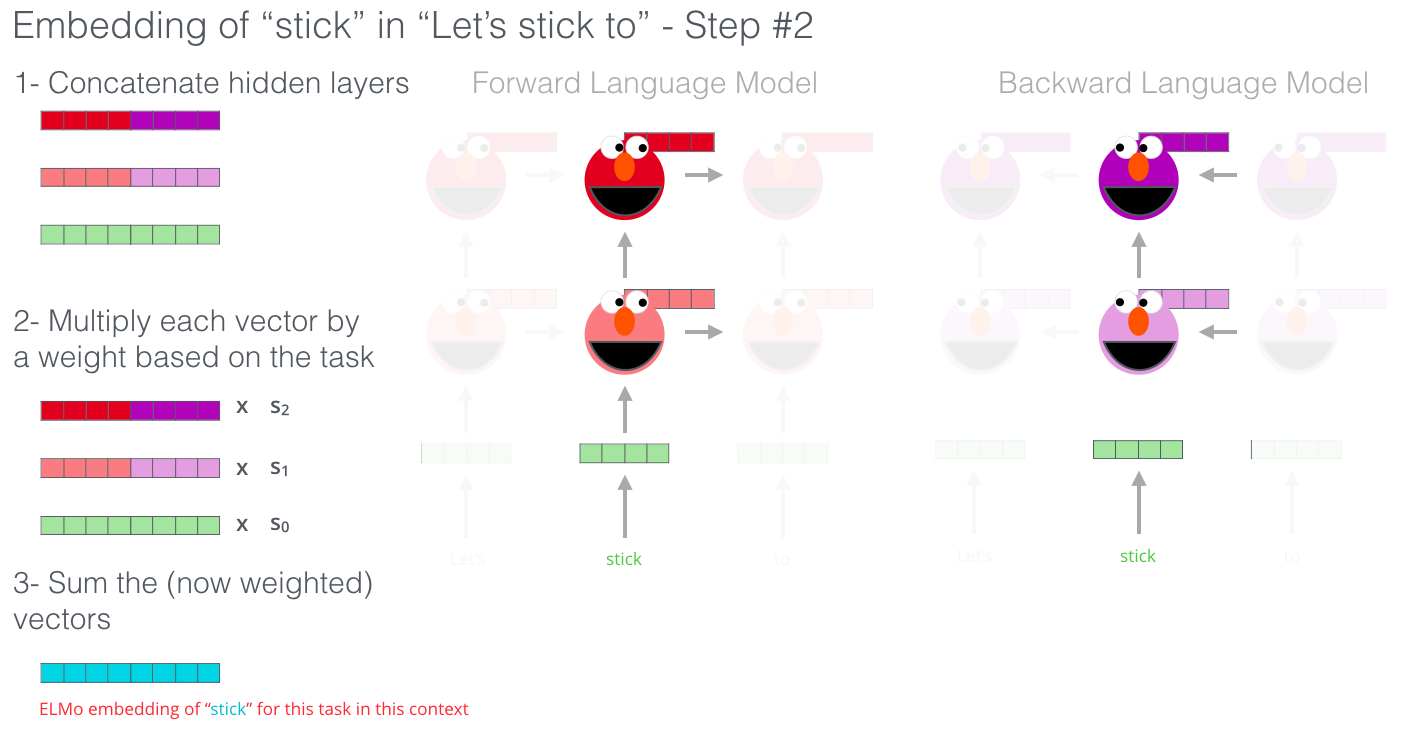
이미지 출처 : http://jalammar.github.io
위 그림에서 $s_0, s_1, s_2$는 학습을 통해 갱신되는 파라미터로 우리가 수행하고자 하는 태스크에 따라 달라집니다. 위에서도 말했던 것처럼 단어의 문맥적인 의미가 중요한 태스크에서는 상위 레이어에 곱해주는 $s_2$가 커지게 되고, 구조 관계가 중요한 태스크에서는 하위 레이어에 곱해주는 $s_1$이 커지게 됩니다.
아래는 이 과정을 수식 기호를 사용하여 보여주는 그림입니다. 아래 그림에서 $t_k$는 $k$번째 단어 토큰을 나타내며 $\mathbf{x}_k$는 토큰의 임베딩 벡터를 나타냅니다. $\overrightarrow{\mathbf{h}_k^{LM}}, \overleftarrow{\mathbf{h}_k^{LM}}$는 각각 $k$번째 토큰에 대한 순방향 및 역방향 LM의 은닉 벡터를 나타내며 둘을 Concatenate하여 $[\overrightarrow{\mathbf{h}_k^{LM}}; \overleftarrow{\mathbf{h}_k^{LM}}] = \mathbf{h}_k^{LM}$ 이 됩니다. $\gamma$는 세 벡터를 가중합하여 나온 최종 벡터의 요소를 얼마나 증폭 혹은 감소시킬 것인지에 대한 Scale factor이며 태스크에 따라서 달라지게 됩니다.

이미지 출처 : zhangruochi.com
biLM
수식을 통해 ELMo를 구성하고 있는 양방향 언어 모델(Bidirectional Language Model, biLM)에 대해 알아보겠습니다. 기호는 위에서 사용했던 것을 그대로 사용합니다. 지금까지 알아보았던 순방향으로 진행되는 언어 모델에서 특정한 $N$개의 단어로 구성된 문장을 만드는 확률을 아래와 같이 나타낼 수 있었습니다.
[P(t_1,t_2, \cdots, t_N) = \prod_{k=1}^N P(t_k
t_1, t_2, \cdots, t_{k-1})]
ELMo에서 입력 토큰 벡터에 해당하는 $\mathbf{x}_k^{\text{LM}}$는 단어 단위의 임베딩 모델에서 Pretrained 된 임베딩 벡터를 그대로 가져와서 사용합니다. 하지만 LSTM이 토큰 임베딩을 학습하여 나타나는 은닉 상태 벡터인 $\overrightarrow{\mathbf{h}_k^{LM}}$은 문맥을 고려할 수 있게 됩니다. 역방향에섣 마찬가지 입니다. 역방향 모델을 수식으로 나타내면 다음과 같습니다.
[P(t_1,t_2, \cdots, t_N) = \prod_{k=1}^N P(t_k
t_{k+1}, t_{k+2}, \cdots, t_{N})]
역방향 언어 모델에서는 타겟 토큰 $t_k$보다 뒤에 위치하는 토큰이 조건으로 주어지며 이로부터 $t_k$를 예측하게 됩니다. 역방향 LSTM에 의해 생성된 은닉 상태 벡터 $\overleftarrow{\mathbf{h}_k^{LM}}$역시 문맥을 고려할 수 있습니다. 이제 이 두 방향을 결합, 즉 두 식을 곱한 후에 $t_k$가 위치할 최대 우도(Maximum Likelihood)를 구하면 되겠습니다.
[\prod_{k=1}^N P(t_k
t_1, t_2, \cdots, t_{k-1}) \times \prod_{k=1}^N P(t_k
t_{k+1}, t_{k+2}, \cdots, t_{N})]
위 식에 로그를 취해주면 다음과 같은 식이 나오게 됩니다. 아래 식에서 $\Theta_X, \Theta_s$는 토큰 벡터 층과 소프트맥스 층에서 사용되는 파라미터를 가리키는 것으로 두 방향 모두에 같은 파라미터가 적용됩니다. ${\Theta}_{LSTM}$은 각 방향 LSTM층에서 사용되는 파라미터로 방향마다 다른 파라미터가 학습됩니다.
[\begin{aligned}
\sum^N_{k=1} \bigg( &\log P(t_k|t_1, t_2, \cdots, t_{k-1}; \Theta_x, \overrightarrow{\Theta}_{LSTM} , \Theta_s)\
- &\log P(t_k|t_{k+1}, t_{k+2}, \cdots, t_N; \Theta_x, \overleftarrow{\Theta}_{LSTM} , \Theta_s) \bigg)
\end{aligned}]
$L$개의 층을 가진 양방향 언어 모델을 통해서 생성된 $L$개의 은닉 벡터 $\overrightarrow{\mathbf{h}_k^{LM}}, \overleftarrow{\mathbf{h}_k^{LM}}$를 이어붙이고(Concatenate) 최초의 임베딩 토큰 벡터 $\mathbf{x}_k^{\text{LM}}$를 자기 자신과 이어 붙인 벡터의 집합을 $R_k$라고 하겠습니다.
[R_k = {\mathbf{x}k^{LM}, \overrightarrow{\mathbf{h}{k,j}^{LM}}, \overleftarrow{\mathbf{h}_{k,j}^{LM}}
j = 1, \cdots, L} = {\mathbf{h}_{k,j}^{LM}
j=0, \cdots, L}]
이어붙인 $L+1$개의 토큰을 선형 결합한 뒤에 최종 ELMo벡터가 만들어지게 됩니다. 선형 결합시에 사용되는 가중치 $s$는 ELMo를 사용하고자 하는 태스크에 따라 달라지게 됩니다. $\gamma$는 벡터 요소의 크기를 조정하는 Scale factor로 역시 태스크에 따라 변하게 됩니다.
[\text{ELMo}k^\text{task} = E(R_k;\Theta^\text{task}) = \gamma^\text{task} \sum^L{j=0} s_j^\text{task} h_{k,j}^{LM}]
Evaluation
아래는 다양한 태스크에서 ELMo가 보여준 성능을 기록한 것입니다. 몇몇 태스크에 대하여 당시의 SOTA 모델보다 좋은 성능을 보였음을 알 수 있습니다.

이미지 출처 : Deep contextualized word representations
아래는 “임베딩 벡터와 은닉 벡터에 가중치를 어떻게 부여할 것인가?”에 대한 연구결과를 이미지로 나타낸 것입니다. 논문에서 적용했던 것과 같이 $L+1$개의 벡터에 모두 다른 가중치를 적용할 때의 성능이 가장 좋은 것을 볼 수 있습니다. 이는 두 번째인 가중치를 적용하지 않을 때보다 더 좋은 성능을 보여주고 있습니다. 벡터의 선형 결합을 사용하지 않고 하나의 벡터만 사용한다면 $L$번째 층, 즉 최상단 은닉층이 생성한 벡터를 사용하는 것이 그냥 단어 임베딩 벡터를 사용하는 것보다 좋다는 연구 결과가 있습니다.

이미지 출처 : Text Analytics 강의자료
아래 그림은 “ELMo 임베딩 벡터를 어떤 단계에 Concatenate하는 것이 좋은가?”에 대한 연구결과입니다. 입출력 단계에 모두 ELMo 임베딩을 적용하는 것이 가장 좋은 것을 볼 수 있습니다. 입, 출력 벡터 중 하나에만 적용하는 경우는 모두 적용한 경우보다는 떨어지지만, 아무것도 사용하지 않은 모델보다는 좋은 성능을 보여주는 것을 알 수 있습니다.

이미지 출처 : Text Analytics 강의자료
ELMo를 시작으로 대량의 말뭉치로부터 생성된 품질 좋은 임베딩 벡터를 만드는 모델이 많이 사용되었습니다. ELMo는 이후에 등장하는 트랜스포머 기반의 BERT나 GPT보다 많이 사용되지는 않습니다. 하지만 좋은 품질의 임베딩 벡터를 바탕으로 적절한 Fine-tuning후에 여러 태스크에 적용하는 전이 학습(Transfer learning)의 시초격인 모델로서의 의의가 있다고 할 수 있겠습니다.
본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 책을 참고하였습니다.
ELMo

이미지 출처 : 트위터 - Elmo
ELMo(Embeddings from Language Models)는 2018년 6월에 “Deep contextualized word representations” 논문을 통해 발표된 임베딩 모델입니다. “Embeddings from Language Models”라는 말 그대로 언어 모델로부터 만들어진 임베딩이며 더 좋은 단어 표현(Representation)을 위해 만들어졌습니다.
논문에서는 좋은 단어 표현의 조건으로 두 가지를 제시하고 있습니다. 첫 번째는 단어의 구조(Syntax)적 특성과 의미(Semantic)적 특성을 모두 만족시키는 표현이어야 합니다. 두 번째는 언어학적으로 문맥에 맞는 표현을 할 수 있어야 합니다. 아래는 “stick”이라는 표현에 대한 임베딩을 ELMo에게 부탁하는 장면입니다.

이미지 출처 : http://jalammar.github.io
이전 모델에서는 “stick”이라는 단어를 보면 문맥상 의미는 배제한 채 말뭉치에서 학습한 대로 임베딩했습니다. 하지만 엘모는 단어만 가지고는 답을 주지 않습니다. 엘모는 그 단어가 쓰인 문장이 어떤 것이며 단어가 그 문장에서 어떤 구조나 의미를 가지고 있는지를 알아야 임베딩 벡터를 내놓게 됩니다.
ELMo(biLM)과 GloVe를 비교한 하나의 예시를 더 보겠습니다. 아래 그림에서는 각 임베딩 모델로부터 “play”와 비슷한 단어를 나타낸 결과입니다.

이미지 출처 : slideshare.net/shuntaroy
위 그림에서 GloVe로 임베딩하면 “play”라는 단어와 비슷한 단어를 뽑았을 때 “playing, game, games, players …” 등 스포츠와 관련된 단어들이 있는 것을 알 수 있습니다. 하지만 ELMo는 “play”가 문장에서 어떤 의미로 사용되었는 지를 구분합니다. 표에서 2행에 있는 “play”는 GloVe가 판단한 것과 동일한 “(스포츠)경기”를 의미하고 있으며 마지막 행에 있는 “(a Broadway) play”를 의미하고 있습니다. ELMo는 이를 문맥에 맞게 잘 판단하고 있는 것을 볼 수 있습니다.
bi-LSTM
ELMo는 문장을 입력받아 단어 토큰의 임베딩 벡터를 만듭니다. 이런 점에서 단어나 서브워드를 입력받았던 Word2Vec, GloVe, Fasttext 등의 이전 모델과 차이점을 갖습니다. 커다란 말뭉치를 2개 층으로 이루어진 bi-LSTM(bidirectional LSTM, 양방향 LSTM)이 만들어내는 임베딩 벡터를 사용합니다.
이 벡터는 bi-LSTM의 내부 층에 대한 은닉 벡터(Hidden vector)에 가중치를 부여한 뒤에 선형 결합(Linear combination)하여 사용합니다. 이렇게 선형 결합을 통해 나타나는 벡터는 단어가 가진 많은 특성에 대한 정보를 담고 있게 됩니다. 각 은닉 벡터 중에서 위쪽에 위치한 LSTM은 단어의 문맥적인(Context-dependent) 의미를 포착할 수 있고 아래쪽에 위치한 LSTM은 단어의 구조적인(Syntax) 의미를 포착할 수 있습니다.
따라서 단어의 구조적인 표현이 중요해지는 구문 분석(Syntax Analysis)이나 품사 태깅(POS Tagging) 등의 태스크에는 아래쪽 biLSTM층이 만들어 내는 은닉 벡터에 가중치를 더 많이 주게 됩니다. 반대로 의미적인 표현이 중요해지는 NLU(Natural Language Understanding)이나 QA(Question&Answering) 등의 태스크에는 위쪽 biLSTM층이 만들어 내는 은닉 벡터에 더 많은 가중치를 부여하게 되지요.
ELMo는 전체 문장을 본 후에 문장을 구성하는 단어에 임베딩을 해줍니다. 아래는 “Let’s stick to improvisation in this skit”이라는 문장을 입력했을 때 단어가 임베딩되는 과정을 도식화하여 보여주고 있습니다.

이미지 출처 : http://jalammar.github.io
ELMo는 기본적으로 언어 모델(Language Models)을 따르고 있기 때문에 타겟 단어 이전까지의 시퀀스로부터 타겟 단어를 예측합니다. 아래는 “Let’s stick to improvisation in this skit”에서 ELMo가 “improvisation”을 예측하는 과정을 보여주는 이미지입니다. (엘모는 귀엽습니다)

이미지 출처 : http://jalammar.github.io
ELMo는 단방향으로의 LSTM이 아니라 biLSTM, 즉 양방향으로 진행하는 LSTM을 사용하여 학습합니다. 아래는 ELMo가 입력 문장을 양방향으로 읽어 나간다는 것을 도식화한 이미지입니다. (엘모는 보라색도 귀엽습니다)

이미지 출처 : http://jalammar.github.io
이후에는 단어마다 순방향(Forward) LSTM의 은닉 벡터 및 토큰 임베딩 벡터와 역방향(Backward) LSTM의 은닉 벡터 및 토큰 임베딩 벡터를 Concatenate합니다. 그리고 이어붙인 벡터에 각각 가중치 $s_0, s_1, s_2$ 를 곱해줍니다. 마지막으로 세 벡터를 더해준 벡터를 ELMo 임베딩 벡터로 사용합니다. 아래는 이 “stick”이라는 단어가 ELMo 임베딩 되는 과정을 보여주고 있습니다.

이미지 출처 : http://jalammar.github.io
위 그림에서 $s_0, s_1, s_2$는 학습을 통해 갱신되는 파라미터로 우리가 수행하고자 하는 태스크에 따라 달라집니다. 위에서도 말했던 것처럼 단어의 문맥적인 의미가 중요한 태스크에서는 상위 레이어에 곱해주는 $s_2$가 커지게 되고, 구조 관계가 중요한 태스크에서는 하위 레이어에 곱해주는 $s_1$이 커지게 됩니다.
아래는 이 과정을 수식 기호를 사용하여 보여주는 그림입니다. 아래 그림에서 $t_k$는 $k$번째 단어 토큰을 나타내며 $\mathbf{x}_k$는 토큰의 임베딩 벡터를 나타냅니다. $\overrightarrow{\mathbf{h}_k^{LM}}, \overleftarrow{\mathbf{h}_k^{LM}}$는 각각 $k$번째 토큰에 대한 순방향 및 역방향 LM의 은닉 벡터를 나타내며 둘을 Concatenate하여 $[\overrightarrow{\mathbf{h}_k^{LM}}; \overleftarrow{\mathbf{h}_k^{LM}}] = \mathbf{h}_k^{LM}$ 이 됩니다. $\gamma$는 세 벡터를 가중합하여 나온 최종 벡터의 요소를 얼마나 증폭 혹은 감소시킬 것인지에 대한 Scale factor이며 태스크에 따라서 달라지게 됩니다.

이미지 출처 : zhangruochi.com
biLM
수식을 통해 ELMo를 구성하고 있는 양방향 언어 모델(Bidirectional Language Model, biLM)에 대해 알아보겠습니다. 기호는 위에서 사용했던 것을 그대로 사용합니다. 지금까지 알아보았던 순방향으로 진행되는 언어 모델에서 특정한 $N$개의 단어로 구성된 문장을 만드는 확률을 아래와 같이 나타낼 수 있었습니다.
| [P(t_1,t_2, \cdots, t_N) = \prod_{k=1}^N P(t_k | t_1, t_2, \cdots, t_{k-1})] |
ELMo에서 입력 토큰 벡터에 해당하는 $\mathbf{x}_k^{\text{LM}}$는 단어 단위의 임베딩 모델에서 Pretrained 된 임베딩 벡터를 그대로 가져와서 사용합니다. 하지만 LSTM이 토큰 임베딩을 학습하여 나타나는 은닉 상태 벡터인 $\overrightarrow{\mathbf{h}_k^{LM}}$은 문맥을 고려할 수 있게 됩니다. 역방향에섣 마찬가지 입니다. 역방향 모델을 수식으로 나타내면 다음과 같습니다.
| [P(t_1,t_2, \cdots, t_N) = \prod_{k=1}^N P(t_k | t_{k+1}, t_{k+2}, \cdots, t_{N})] |
역방향 언어 모델에서는 타겟 토큰 $t_k$보다 뒤에 위치하는 토큰이 조건으로 주어지며 이로부터 $t_k$를 예측하게 됩니다. 역방향 LSTM에 의해 생성된 은닉 상태 벡터 $\overleftarrow{\mathbf{h}_k^{LM}}$역시 문맥을 고려할 수 있습니다. 이제 이 두 방향을 결합, 즉 두 식을 곱한 후에 $t_k$가 위치할 최대 우도(Maximum Likelihood)를 구하면 되겠습니다.
| [\prod_{k=1}^N P(t_k | t_1, t_2, \cdots, t_{k-1}) \times \prod_{k=1}^N P(t_k | t_{k+1}, t_{k+2}, \cdots, t_{N})] |
위 식에 로그를 취해주면 다음과 같은 식이 나오게 됩니다. 아래 식에서 $\Theta_X, \Theta_s$는 토큰 벡터 층과 소프트맥스 층에서 사용되는 파라미터를 가리키는 것으로 두 방향 모두에 같은 파라미터가 적용됩니다. ${\Theta}_{LSTM}$은 각 방향 LSTM층에서 사용되는 파라미터로 방향마다 다른 파라미터가 학습됩니다.
[\begin{aligned} \sum^N_{k=1} \bigg( &\log P(t_k|t_1, t_2, \cdots, t_{k-1}; \Theta_x, \overrightarrow{\Theta}_{LSTM} , \Theta_s)\
- &\log P(t_k|t_{k+1}, t_{k+2}, \cdots, t_N; \Theta_x, \overleftarrow{\Theta}_{LSTM} , \Theta_s) \bigg) \end{aligned}]
$L$개의 층을 가진 양방향 언어 모델을 통해서 생성된 $L$개의 은닉 벡터 $\overrightarrow{\mathbf{h}_k^{LM}}, \overleftarrow{\mathbf{h}_k^{LM}}$를 이어붙이고(Concatenate) 최초의 임베딩 토큰 벡터 $\mathbf{x}_k^{\text{LM}}$를 자기 자신과 이어 붙인 벡터의 집합을 $R_k$라고 하겠습니다.
| [R_k = {\mathbf{x}k^{LM}, \overrightarrow{\mathbf{h}{k,j}^{LM}}, \overleftarrow{\mathbf{h}_{k,j}^{LM}} | j = 1, \cdots, L} = {\mathbf{h}_{k,j}^{LM} | j=0, \cdots, L}] |
이어붙인 $L+1$개의 토큰을 선형 결합한 뒤에 최종 ELMo벡터가 만들어지게 됩니다. 선형 결합시에 사용되는 가중치 $s$는 ELMo를 사용하고자 하는 태스크에 따라 달라지게 됩니다. $\gamma$는 벡터 요소의 크기를 조정하는 Scale factor로 역시 태스크에 따라 변하게 됩니다.
[\text{ELMo}k^\text{task} = E(R_k;\Theta^\text{task}) = \gamma^\text{task} \sum^L{j=0} s_j^\text{task} h_{k,j}^{LM}]
Evaluation
아래는 다양한 태스크에서 ELMo가 보여준 성능을 기록한 것입니다. 몇몇 태스크에 대하여 당시의 SOTA 모델보다 좋은 성능을 보였음을 알 수 있습니다.

이미지 출처 : Deep contextualized word representations
아래는 “임베딩 벡터와 은닉 벡터에 가중치를 어떻게 부여할 것인가?”에 대한 연구결과를 이미지로 나타낸 것입니다. 논문에서 적용했던 것과 같이 $L+1$개의 벡터에 모두 다른 가중치를 적용할 때의 성능이 가장 좋은 것을 볼 수 있습니다. 이는 두 번째인 가중치를 적용하지 않을 때보다 더 좋은 성능을 보여주고 있습니다. 벡터의 선형 결합을 사용하지 않고 하나의 벡터만 사용한다면 $L$번째 층, 즉 최상단 은닉층이 생성한 벡터를 사용하는 것이 그냥 단어 임베딩 벡터를 사용하는 것보다 좋다는 연구 결과가 있습니다.

이미지 출처 : Text Analytics 강의자료
아래 그림은 “ELMo 임베딩 벡터를 어떤 단계에 Concatenate하는 것이 좋은가?”에 대한 연구결과입니다. 입출력 단계에 모두 ELMo 임베딩을 적용하는 것이 가장 좋은 것을 볼 수 있습니다. 입, 출력 벡터 중 하나에만 적용하는 경우는 모두 적용한 경우보다는 떨어지지만, 아무것도 사용하지 않은 모델보다는 좋은 성능을 보여주는 것을 알 수 있습니다.

이미지 출처 : Text Analytics 강의자료
ELMo를 시작으로 대량의 말뭉치로부터 생성된 품질 좋은 임베딩 벡터를 만드는 모델이 많이 사용되었습니다. ELMo는 이후에 등장하는 트랜스포머 기반의 BERT나 GPT보다 많이 사용되지는 않습니다. 하지만 좋은 품질의 임베딩 벡터를 바탕으로 적절한 Fine-tuning후에 여러 태스크에 적용하는 전이 학습(Transfer learning)의 시초격인 모델로서의 의의가 있다고 할 수 있겠습니다.