단어 임베딩 (Word Embedding)과 신경망 언어 모델 (NPLM)
24 May 2020 | NLP
본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 책을 참고하였습니다.
Distributed Representation
지금까지 알아본 Bag of Words, TF-IDF, N-gram 방법론은 단어를 등장 횟수 기반으로 벡터로 표현(Count-based representation)하는 방식이었습니다. 이번에는 등장 횟수가 아닌 단어의 분산 표현(Distributed representation)방법에 대해 알아볼 것입니다.
횟수 기반 표현을 사용하지 않고 단어를 벡터화하는 가장 단순하고 직관적인 방법은 원-핫 인코딩(One-hot Encoding)입니다. 원-핫 인코딩은 적용하는 방법은 다음과 같습니다. 일단 문서에 존재하는 단어의 개수 만큼의 차원을 가진 영벡터를 만듭니다. 그리고 단어가 등장하는 순서에 따라 해당 인덱스를 1로 변환한 뒤 그 단어의 벡터로 매칭시켜줍니다. 예를 들어, “What’s your name? My name is Yngie.” 라는 문장에 있는 단어를 원-핫 인코딩을 사용하여 벡터로 표현하면 다음과 같습니다.
\[\begin{aligned}
\text{what} : \left[{\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \end{array}}\right] \\
\text{is} : \left[{\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \end{array}}\right] \\
\text{your} : \left[{\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \end{array}}\right] \\
\text{name} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right] \\
\text{my} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 1 & 0 \end{array}}\right] \\
\text{Yngie} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 1 \end{array}}\right]
\end{aligned}\]
원-핫 인코딩은 단순하고 이해하기 쉽다는 장점이 있습니다. 하지만 단어끼리의 관계를 모사할 수가 없게 됩니다. 벡터 간 유사도를 판단하는 방법은 다양하지만, 단어 벡터 사이의 유사도를 판단하는 데에는 주로 코사인 유사도(Cosine similarity)가 사용됩니다. 코사인 유사도의 수식은 다음과 같습니다.
\[\text{similarity}(\vec{x},\vec{y}) = \frac{\vec{x} \cdot \vec{y}}{\Vert\vec{x}\Vert \Vert\vec{y}\Vert} = \frac{x_1y_1 + \cdots + x_ny_n}{\sqrt{x_1^2+\cdots+x_n^2} \sqrt{y_1^2+\cdots+y_n^2}}\]
원-핫 인코딩으로 생성된 임의의 서로 다른 두 단어 벡터 $\vec{x_o}, \vec{y_o}$ 의 단어간 유사도를 구하기 위해 코사인 유사도 식에 대입하면 어떻게 될까요? 결과만 보자면 모두 0이 나오게 됩니다. 원-핫 인코딩으로 생성된 서로 다른 벡터를 내적한 값 $\vec{x_o} \cdot \vec{y_o}$ 은 언제나 0이 나오기 때문입니다. 이 때문에 원-핫 인코딩은 단어의 의미 관계를 전혀 표현하지 못하게 됩니다.
이런 문제를 해결하기 위해서 분산 표현 방식인 단어 임베딩(Word Embedding)이 고안되었습니다. 임베딩은 단어를 문서 내 단어의 개수 $\vert V \vert$보다 훨씬 작은 숫자인 $n$ 차원의 벡터로 나타냅니다. 임베딩을 통해 나타내어지는 단어 벡터는 성분이 0, 1이 아닌 연속적인 숫자로 구성되어 있습니다. 그렇기 때문에 단어 벡터끼리 내적하여도 0이 아니게 되며 단어 간의 의미(Semantic) 관계가 보존된다는 장점을 가지고 있습니다. 아래 그림은 임베딩을 통해 추출해낸 단어 벡터 간의 관계를 시각화한 것입니다.
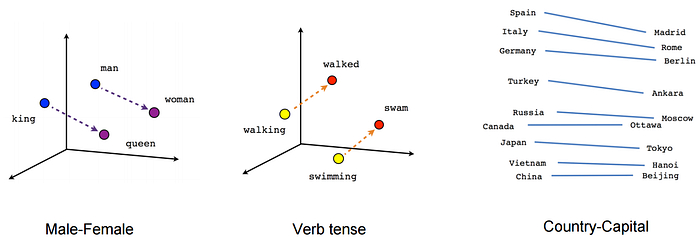
이미지 출처 : towardsdatascience.com
Neural Probabilistic Language Model
확률론적 신경망 언어 모델(Neural Probabilistic Language Model, NPLM)은 기존 단어 횟수 기반의 언어 모델(Language models)의 단점을 극복하고자 만들어진 방법입니다.
신경망 언어 모델에서 각 단어는 임베딩을 통해 $n$ 차원의 벡터로 표현됩니다. 이 단어 벡터를 언어 모델에 적용했을 때의 장점은 무엇일까요? 기존의 언어 모델은 횟수를 기반으로 등장 확률을 결정하기 때문에 말뭉치에 한 번도 등장하지 않은 시퀀스에 대해서는 등장 확률이 0이 된다는 단점이 있었습니다. 예를 들어, “마라룽샤를 요리하다.” 라는 단어 시퀀스가 말뭉치에 등장하지 않는다면 이 시퀀스가 생성될 확률 역시 0이 됩니다.
하지만 임베딩을 통해 표현된 단어 벡터는 의미 관계를 가지고 있기 때문에 다릅니다. 예를 들어, (마라탕, 마라샹궈, 마라룽샤)라는 세 단어묶음, (요리하다, 먹다) 의 관계가 비슷하다고 학습한 모델이 있다고 합시다. 이 모델은 말뭉치에 “마라탕을 먹다” 라는 시퀀스만 있더라도 “마라샹궈를 먹다, 마라탕을 요리하다, 마라룽샤를 먹다, 마라룽샤를 요리하다” 등 다양한 단어 시퀀스를 생성할 수 있게 됩니다. 이제 더 이상 말뭉치 시퀀스에 집착하지 않아도 되는 것이지요.
모델 학습
확률론적 신경망 언어 모델은 기본적으로 N-gram 방식을 사용하여 단어를 추론합니다. 즉, 타겟 단어의 확률을 구하기 위한 조건으로 이전 $N-1$ 개의 단어 벡터를 고려합니다. 아래 그림은 모델의 구조를 이미지로 나타낸 것입니다.

이미지 출처 : imgur.com
먼저 입력 벡터 신경망에 들어갈 $\mathbf{x_t}$ 가 어떻게 생성되는지 알아보겠습니다. 이 과정은 커다란 행렬 $C$ 에서 타겟 단어인 $w_t$ 를 참조(look-up)하는 방식으로 이루어집니다. 위 그림에서도 각 단어인 $w$ 에 맞는 행을 참조 $C(w)$ 하여 벡터화하는 것을 볼 수 있습니다. 전체 $\vert V \vert$ 개 단어 모두를 $n$ 차원 벡터로 나타내기 위해 참조하는 것이므로 $C$ 의 크기는 $\vert V \vert \times n$ 이 됩니다.
실제의 연산은 모든 단어를 원-핫 인코딩을 통해 원-핫 벡터 $w_t$ 로 나타낸 뒤에 $C$ 와 내적하는 과정으로 이루어집니다. 원-핫 인코딩에서 사용했던 “What’s your name? My name is Yngie.” 문장을 예시로 다시 가져와보겠습니다.
\[\begin{aligned}
\text{what} : \left[{\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \end{array}}\right] \\
\text{is} : \left[{\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \end{array}}\right] \\
\text{your} : \left[{\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \end{array}}\right] \\
\text{name} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right] \\
\text{my} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 1 & 0 \end{array}}\right] \\
\text{Yngie} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 1 \end{array}}\right]
\end{aligned}\]
이 단어를 5차원 벡터로 나타내려면 참조할 행렬 $C$ 의 사이즈는 어떻게 되어야 할까요? 단어의 개수 $\vert V\vert = 6$ 이고 나타내고자 하는 임베딩 벡터의 차원 $n = 5$ 이므로 $6 \times 5$ 가 되어야 하겠습니다. 행렬 $C$ 의 성분은 정해져 있는 것이 아니고 초기에 임의의 값을 넣어준 후 학습 과정에서 갱신되는 것이므로 임의의 값을 넣어 만들어 보겠습니다.
\[C : \left[{\begin{array}{ccccc} 10 & 2 & 3 & 2 & 4 \\
4 & 9 & 7 & 3 & 5 \\ 1 & 4 & 11 & 3 & 7 \\ 7 & 7 & 5 & 4 & 2 \\ 9 & 8 & 3 & 2 & 5 \\ 8 & 2 & 3 & 1 & 7 \end{array}}\right]\]
단어의 원-핫 벡터 $w_t$ 와 $C$ 를 내적하면 각 단어의 벡터 $\mathbf{x}_t$ 를 구할 수 있게 됩니다. $C$ 의 각 행이 단어 벡터가 되는 것을 알 수 있습니다. 예를 들어, “name” 의 임베딩 벡터 $\mathbf{x}_4$ 가 만들어지는 과정을 보겠습니다.
\[\left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right] \cdot \left[{\begin{array}{ccccc} 10 & 2 & 3 & 2 & 4 \\
4 & 9 & 7 & 3 & 5 \\ 1 & 4 & 11 & 3 & 7 \\ 7 & 7 & 5 & 4 & 2 \\ 9 & 8 & 3 & 2 & 5 \\ 8 & 2 & 3 & 1 & 7 \end{array}}\right] = \left[{\begin{array}{ccccc} 7 & 7 & 5 & 4 & 2 \end{array}}\right]\]
N-gram 방식을 사용하여 타겟 단어의 확률을 예측하기 때문에 입력 데이터는 $N-1$ 개의 단어 벡터가 됩니다. 예를 들어, “What’s your name? My name is Yngie.” 라는 문장에서 첫 번째 “name” 을 Tri-gram, 즉 $N=3$ 으로 예측한다면 “is, your” 의 임베딩 벡터를 입력하게 되므로 입력 데이터는 다음과 같아집니다. 아래 식에서 $\mathbf{x_2}, \mathbf{x_3}$ 는 각각 “is” 와 “your” 의 임베딩 벡터를 나타낸 것입니다.
\[\therefore \mathbf{x} = [\mathbf{x}_2, \mathbf{x}_3] = [\left[{\begin{array}{ccccc} 4 & 9 & 7 & 3 & 5 \end{array}}\right], \left[{\begin{array}{ccccc} 1 & 4 & 11 & 3 & 7 \end{array}}\right]\]
은닉층에 들어간 입력 벡터는 다음의 함수를 거쳐 출력층에 들어가는 벡터 $\mathbf{y}_{w_t}$ 가 됩니다.
\[\mathbf{y}_{w_t} = b + W\mathbf{x} + U\cdot\tanh(d+H\mathbf{x})\]
$W$ 는 단어 벡터 자체에 부여되는 가중치 행렬이고 $H$ 는 은닉층에서 단어 벡터에 가해지는 가중치입니다. 위 식에서 출력층에 들어가는 벡터를 생성하는 함수에서 2개의 가중치 행렬 $W, H$ 이 있는 이유는 임베딩 벡터, 즉 참조 테이블 $C$ 와 확률 함수의 변수를 동시에 학습하기 때문입니다. 위에서 본 그림을 다시 가져와보면 가장 왼쪽에 단어 벡터가 바로 출력층으로 바로 들어가는 경로(점선)가 있고, 은닉층을 거쳐 들어가는 경로(실선)가 있는 것을 알 수 있습니다.

이미지 출처 : imgur.com
출력층에서 계산되는 타겟 단어의 확률 $P$ 는 소프트맥스 함수에 의해서 구해집니다. 수식으로 나타내면 다음과 같습니다.
\[P(w_t = j|w_{t-1}, \cdots , w_{t-N+1}) = \frac{\exp(\mathbf{y}_{w_t})}{\sum_{j^\prime \in V} \exp(\mathbf{y}_{w_j^\prime})}\]
학습 이후
확률론적 신경망 언어 모델을 포함한 이후의 언어 모델은 위에서 말했던 것과 같이 단어의 의미 관계를 학습하기 때문에 말뭉치에 등장하지 않는 단어라도 생성해낼 수 있다는 장점이 있습니다. 단순한 예시로 다음과 같은 세 문장이 있는 말뭉치가 있다고 해봅시다.
“there are three teams left for qualification.” , “four teams have passed the first round.”, “four groups are playing in the field.”
신경망 언어 모델은 단어의 관계를 파악하기 때문에 말뭉치에는 없는 “three groups” 라는 단어 시퀀스를 만들어 낼 수 있게 됩니다.
확률론적 신경망 언어 모델은 2003년에 발표된 모델으로서 이후 등장하는 다양한 임베딩 방법보다는 성능이 좋지 않습니다. 하지만 임베딩을 통해 단어의 의미 관계를 보존하는 방식을 제안했다는 점에서 의의가 적지 않습니다.
본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 책을 참고하였습니다.
Distributed Representation
지금까지 알아본 Bag of Words, TF-IDF, N-gram 방법론은 단어를 등장 횟수 기반으로 벡터로 표현(Count-based representation)하는 방식이었습니다. 이번에는 등장 횟수가 아닌 단어의 분산 표현(Distributed representation)방법에 대해 알아볼 것입니다.
횟수 기반 표현을 사용하지 않고 단어를 벡터화하는 가장 단순하고 직관적인 방법은 원-핫 인코딩(One-hot Encoding)입니다. 원-핫 인코딩은 적용하는 방법은 다음과 같습니다. 일단 문서에 존재하는 단어의 개수 만큼의 차원을 가진 영벡터를 만듭니다. 그리고 단어가 등장하는 순서에 따라 해당 인덱스를 1로 변환한 뒤 그 단어의 벡터로 매칭시켜줍니다. 예를 들어, “What’s your name? My name is Yngie.” 라는 문장에 있는 단어를 원-핫 인코딩을 사용하여 벡터로 표현하면 다음과 같습니다.
\[\begin{aligned} \text{what} : \left[{\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \end{array}}\right] \\ \text{is} : \left[{\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \end{array}}\right] \\ \text{your} : \left[{\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \end{array}}\right] \\ \text{name} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right] \\ \text{my} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 1 & 0 \end{array}}\right] \\ \text{Yngie} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 1 \end{array}}\right] \end{aligned}\]원-핫 인코딩은 단순하고 이해하기 쉽다는 장점이 있습니다. 하지만 단어끼리의 관계를 모사할 수가 없게 됩니다. 벡터 간 유사도를 판단하는 방법은 다양하지만, 단어 벡터 사이의 유사도를 판단하는 데에는 주로 코사인 유사도(Cosine similarity)가 사용됩니다. 코사인 유사도의 수식은 다음과 같습니다.
\[\text{similarity}(\vec{x},\vec{y}) = \frac{\vec{x} \cdot \vec{y}}{\Vert\vec{x}\Vert \Vert\vec{y}\Vert} = \frac{x_1y_1 + \cdots + x_ny_n}{\sqrt{x_1^2+\cdots+x_n^2} \sqrt{y_1^2+\cdots+y_n^2}}\]원-핫 인코딩으로 생성된 임의의 서로 다른 두 단어 벡터 $\vec{x_o}, \vec{y_o}$ 의 단어간 유사도를 구하기 위해 코사인 유사도 식에 대입하면 어떻게 될까요? 결과만 보자면 모두 0이 나오게 됩니다. 원-핫 인코딩으로 생성된 서로 다른 벡터를 내적한 값 $\vec{x_o} \cdot \vec{y_o}$ 은 언제나 0이 나오기 때문입니다. 이 때문에 원-핫 인코딩은 단어의 의미 관계를 전혀 표현하지 못하게 됩니다.
이런 문제를 해결하기 위해서 분산 표현 방식인 단어 임베딩(Word Embedding)이 고안되었습니다. 임베딩은 단어를 문서 내 단어의 개수 $\vert V \vert$보다 훨씬 작은 숫자인 $n$ 차원의 벡터로 나타냅니다. 임베딩을 통해 나타내어지는 단어 벡터는 성분이 0, 1이 아닌 연속적인 숫자로 구성되어 있습니다. 그렇기 때문에 단어 벡터끼리 내적하여도 0이 아니게 되며 단어 간의 의미(Semantic) 관계가 보존된다는 장점을 가지고 있습니다. 아래 그림은 임베딩을 통해 추출해낸 단어 벡터 간의 관계를 시각화한 것입니다.

이미지 출처 : towardsdatascience.com
Neural Probabilistic Language Model
확률론적 신경망 언어 모델(Neural Probabilistic Language Model, NPLM)은 기존 단어 횟수 기반의 언어 모델(Language models)의 단점을 극복하고자 만들어진 방법입니다.
신경망 언어 모델에서 각 단어는 임베딩을 통해 $n$ 차원의 벡터로 표현됩니다. 이 단어 벡터를 언어 모델에 적용했을 때의 장점은 무엇일까요? 기존의 언어 모델은 횟수를 기반으로 등장 확률을 결정하기 때문에 말뭉치에 한 번도 등장하지 않은 시퀀스에 대해서는 등장 확률이 0이 된다는 단점이 있었습니다. 예를 들어, “마라룽샤를 요리하다.” 라는 단어 시퀀스가 말뭉치에 등장하지 않는다면 이 시퀀스가 생성될 확률 역시 0이 됩니다.
하지만 임베딩을 통해 표현된 단어 벡터는 의미 관계를 가지고 있기 때문에 다릅니다. 예를 들어, (마라탕, 마라샹궈, 마라룽샤)라는 세 단어묶음, (요리하다, 먹다) 의 관계가 비슷하다고 학습한 모델이 있다고 합시다. 이 모델은 말뭉치에 “마라탕을 먹다” 라는 시퀀스만 있더라도 “마라샹궈를 먹다, 마라탕을 요리하다, 마라룽샤를 먹다, 마라룽샤를 요리하다” 등 다양한 단어 시퀀스를 생성할 수 있게 됩니다. 이제 더 이상 말뭉치 시퀀스에 집착하지 않아도 되는 것이지요.
모델 학습
확률론적 신경망 언어 모델은 기본적으로 N-gram 방식을 사용하여 단어를 추론합니다. 즉, 타겟 단어의 확률을 구하기 위한 조건으로 이전 $N-1$ 개의 단어 벡터를 고려합니다. 아래 그림은 모델의 구조를 이미지로 나타낸 것입니다.

이미지 출처 : imgur.com
먼저 입력 벡터 신경망에 들어갈 $\mathbf{x_t}$ 가 어떻게 생성되는지 알아보겠습니다. 이 과정은 커다란 행렬 $C$ 에서 타겟 단어인 $w_t$ 를 참조(look-up)하는 방식으로 이루어집니다. 위 그림에서도 각 단어인 $w$ 에 맞는 행을 참조 $C(w)$ 하여 벡터화하는 것을 볼 수 있습니다. 전체 $\vert V \vert$ 개 단어 모두를 $n$ 차원 벡터로 나타내기 위해 참조하는 것이므로 $C$ 의 크기는 $\vert V \vert \times n$ 이 됩니다.
실제의 연산은 모든 단어를 원-핫 인코딩을 통해 원-핫 벡터 $w_t$ 로 나타낸 뒤에 $C$ 와 내적하는 과정으로 이루어집니다. 원-핫 인코딩에서 사용했던 “What’s your name? My name is Yngie.” 문장을 예시로 다시 가져와보겠습니다.
\[\begin{aligned} \text{what} : \left[{\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \end{array}}\right] \\ \text{is} : \left[{\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \end{array}}\right] \\ \text{your} : \left[{\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \end{array}}\right] \\ \text{name} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right] \\ \text{my} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 1 & 0 \end{array}}\right] \\ \text{Yngie} : \left[{\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 1 \end{array}}\right] \end{aligned}\]이 단어를 5차원 벡터로 나타내려면 참조할 행렬 $C$ 의 사이즈는 어떻게 되어야 할까요? 단어의 개수 $\vert V\vert = 6$ 이고 나타내고자 하는 임베딩 벡터의 차원 $n = 5$ 이므로 $6 \times 5$ 가 되어야 하겠습니다. 행렬 $C$ 의 성분은 정해져 있는 것이 아니고 초기에 임의의 값을 넣어준 후 학습 과정에서 갱신되는 것이므로 임의의 값을 넣어 만들어 보겠습니다.
\[C : \left[{\begin{array}{ccccc} 10 & 2 & 3 & 2 & 4 \\ 4 & 9 & 7 & 3 & 5 \\ 1 & 4 & 11 & 3 & 7 \\ 7 & 7 & 5 & 4 & 2 \\ 9 & 8 & 3 & 2 & 5 \\ 8 & 2 & 3 & 1 & 7 \end{array}}\right]\]단어의 원-핫 벡터 $w_t$ 와 $C$ 를 내적하면 각 단어의 벡터 $\mathbf{x}_t$ 를 구할 수 있게 됩니다. $C$ 의 각 행이 단어 벡터가 되는 것을 알 수 있습니다. 예를 들어, “name” 의 임베딩 벡터 $\mathbf{x}_4$ 가 만들어지는 과정을 보겠습니다.
\[\left[{\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}}\right] \cdot \left[{\begin{array}{ccccc} 10 & 2 & 3 & 2 & 4 \\ 4 & 9 & 7 & 3 & 5 \\ 1 & 4 & 11 & 3 & 7 \\ 7 & 7 & 5 & 4 & 2 \\ 9 & 8 & 3 & 2 & 5 \\ 8 & 2 & 3 & 1 & 7 \end{array}}\right] = \left[{\begin{array}{ccccc} 7 & 7 & 5 & 4 & 2 \end{array}}\right]\]N-gram 방식을 사용하여 타겟 단어의 확률을 예측하기 때문에 입력 데이터는 $N-1$ 개의 단어 벡터가 됩니다. 예를 들어, “What’s your name? My name is Yngie.” 라는 문장에서 첫 번째 “name” 을 Tri-gram, 즉 $N=3$ 으로 예측한다면 “is, your” 의 임베딩 벡터를 입력하게 되므로 입력 데이터는 다음과 같아집니다. 아래 식에서 $\mathbf{x_2}, \mathbf{x_3}$ 는 각각 “is” 와 “your” 의 임베딩 벡터를 나타낸 것입니다.
\[\therefore \mathbf{x} = [\mathbf{x}_2, \mathbf{x}_3] = [\left[{\begin{array}{ccccc} 4 & 9 & 7 & 3 & 5 \end{array}}\right], \left[{\begin{array}{ccccc} 1 & 4 & 11 & 3 & 7 \end{array}}\right]\]은닉층에 들어간 입력 벡터는 다음의 함수를 거쳐 출력층에 들어가는 벡터 $\mathbf{y}_{w_t}$ 가 됩니다.
\[\mathbf{y}_{w_t} = b + W\mathbf{x} + U\cdot\tanh(d+H\mathbf{x})\]$W$ 는 단어 벡터 자체에 부여되는 가중치 행렬이고 $H$ 는 은닉층에서 단어 벡터에 가해지는 가중치입니다. 위 식에서 출력층에 들어가는 벡터를 생성하는 함수에서 2개의 가중치 행렬 $W, H$ 이 있는 이유는 임베딩 벡터, 즉 참조 테이블 $C$ 와 확률 함수의 변수를 동시에 학습하기 때문입니다. 위에서 본 그림을 다시 가져와보면 가장 왼쪽에 단어 벡터가 바로 출력층으로 바로 들어가는 경로(점선)가 있고, 은닉층을 거쳐 들어가는 경로(실선)가 있는 것을 알 수 있습니다.

이미지 출처 : imgur.com
출력층에서 계산되는 타겟 단어의 확률 $P$ 는 소프트맥스 함수에 의해서 구해집니다. 수식으로 나타내면 다음과 같습니다.
\[P(w_t = j|w_{t-1}, \cdots , w_{t-N+1}) = \frac{\exp(\mathbf{y}_{w_t})}{\sum_{j^\prime \in V} \exp(\mathbf{y}_{w_j^\prime})}\]학습 이후
확률론적 신경망 언어 모델을 포함한 이후의 언어 모델은 위에서 말했던 것과 같이 단어의 의미 관계를 학습하기 때문에 말뭉치에 등장하지 않는 단어라도 생성해낼 수 있다는 장점이 있습니다. 단순한 예시로 다음과 같은 세 문장이 있는 말뭉치가 있다고 해봅시다.
“there are three teams left for qualification.” , “four teams have passed the first round.”, “four groups are playing in the field.”
신경망 언어 모델은 단어의 관계를 파악하기 때문에 말뭉치에는 없는 “three groups” 라는 단어 시퀀스를 만들어 낼 수 있게 됩니다.
확률론적 신경망 언어 모델은 2003년에 발표된 모델으로서 이후 등장하는 다양한 임베딩 방법보다는 성능이 좋지 않습니다. 하지만 임베딩을 통해 단어의 의미 관계를 보존하는 방식을 제안했다는 점에서 의의가 적지 않습니다.

Comments