GBM(Gradient Boosting Machine)
21 Mar 2021 | Machine-Learning
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
Gradient Boosting Machine
이번에 알아볼 그래디언트 부스팅 머신(Gradient Boosting Machine, GBM)은 경사 하강법(Gradient descent)을 결합한 새로운 부스팅(Boosting) 알고리즘입니다. Adaboost는 이전 약한 모델의 오답에 가중치를 부여하여 새로운 모델을 학습하는 방법이었는데요. 그래디언트 부스팅 머신은 잔차(Residual)에 집중합니다. 이 잔차를 최소화하는 과정에서 경사 하강법을 사용하기 때문에 이런 이름이 붙었습니다.
Residual
그래디언트 부스팅 머신이 작동되는 방식에 대해서 알아보겠습니다. 먼저 첫 번째 약한 모델(Weak Model) $f_1(\mathbf{x})$ 를 만듭니다. 다음으로 정답과 예측값의 차이, 즉 잔차 $R_1$ 을 계산합니다.
\[y = f_1(\mathbf{x}) + R_1 \\
R_1 = y - f_1(\mathbf{x})\]
다음으로는 잔차 $R_1$ 을 예측하는 두 번째 약한 모델 $f_2(\mathbf{x})$ 을 만듭니다. 그리고 $R_1$ 과 $f_2(\mathbf{x})$ 의 잔차 $R_2$ 를 구합니다.
\[R_1 = f_2(\mathbf{x}) + R_2 \\
R_2 = R_1 - f_2(\mathbf{x})\]
이렇게 $t$ 번째 약한 모델 $f_t(\mathbf{x})$ 는 $t-1$ 번째의 잔차를 근사하는 함수입니다. 이를 $T$ 번 반복한 뒤 정리하면 다음과 같은 식이 될 것입니다. 첫 $R_1$ 은 꽤 크지만 이를 반복해서 근사하는 모델을 더해나가면 마지막 잔차 $R_T$ 는 매우 작아집니다.
\[y = f_1(\mathbf{x}) + f_2(\mathbf{x}) + \cdots + f_T(\mathbf{x}) + R_{T}\]
만약 오차로 평균 제곱 오차(Mean square error, MSE)를 사용하는 회귀 문제라면 아래 이미지와 같이 생각해 볼 수도 있겠습니다.

이미지 출처 : github.com/topics/gradient-boosting-machine
반복 과정동안 잔차를 줄이는 것이 목적이므로 경사 하강법을 사용하여 잔차를 반복해서 줄여나갑니다. 아래는 Stump Tree를 약한 모델로 하는 그래디언트 부스팅 머신으로 회귀 함수를 근사하는 예시입니다. 아래는 1~3회 반복했을 때의 근사 함수와 잔차를 나타낸 이미지입니다.
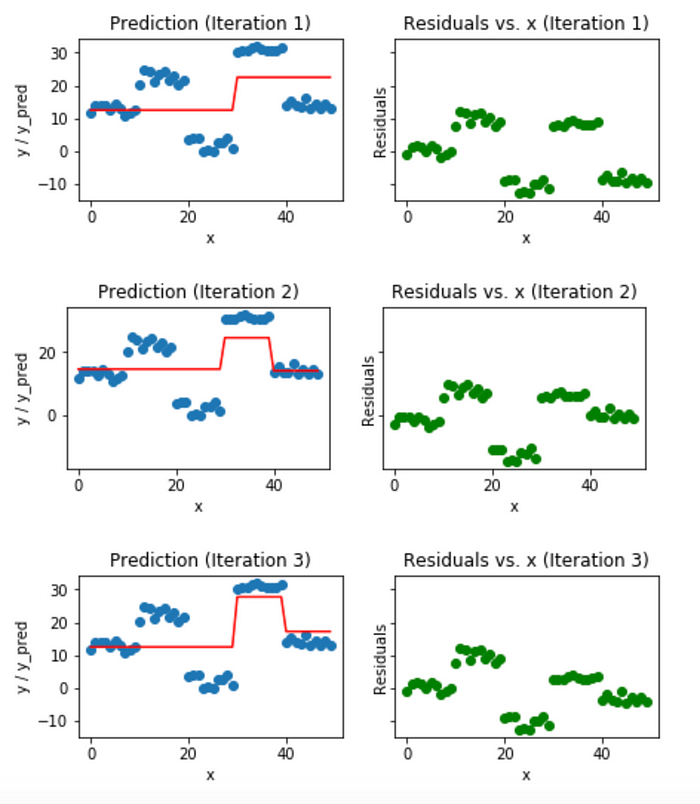
이미지 출처 : medium.com/mlreview
낮은 반복수에서는 잔차가 꽤 크게 나오고 있습니다. 동일한 반복을 계속하면 함수 개형과 잔차가 어떻게 변하는 지 알아보겠습니다. 아래는 18~20회 반복했을 때의 근사 함수와 잔차를 나타낸 이미지입니다.
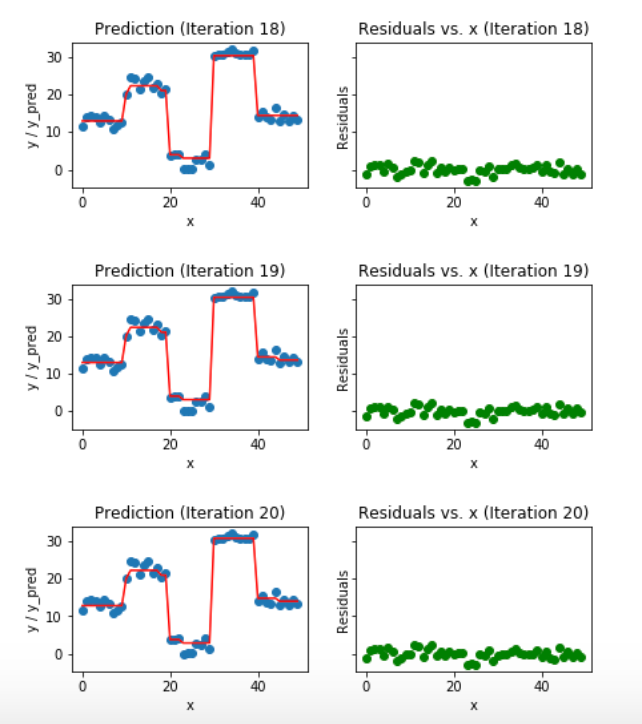
이미지 출처 : medium.com/mlreview
이전보다 잔차가 훨씬 더 줄어든 것을 볼 수 있습니다. 자세히 보면 함수도 좀 더 구불구불해진 것도 볼 수 있습니다. 동일한 과정을 50번 반복하면 아래와 같이 잔차가 더 줄어들고 함수도 더 복잡해집니다.
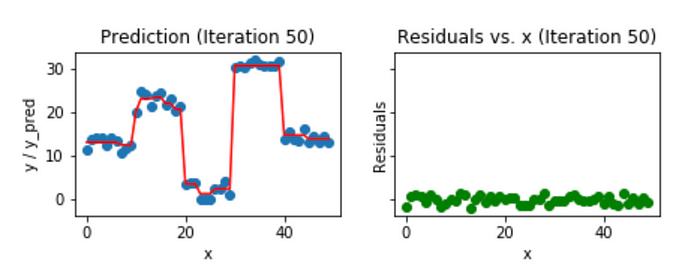
이미지 출처 : medium.com/mlreview
Loss Function
손실 함수(Loss function)의 기울기를 최소화하는 방향으로 추가적인 모델이 순차적으로 생성되기 때문에 어떤 손실 함수를 사용하는 지에 따라 최종으로 생성되는 함수가 달라집니다. 크게는 풀고자하는 문제가 회귀인지 분류인지에 따라서 다른 선택지를 갖게 됩니다.
Regression
회귀를 위한 손실 함수는 제곱 오차, 절대 오차, Huber 오차, Quantile 오차 등이 있습니다. 각각의 식은 아래와 같으며 일반적으로는 제곱 오차 $(L_2)$ 를 많이 사용합니다.
Loss Function
Formula
Squared Loss $(L_2)$
$\Psi(y,f)_{L_2} = \frac{1}{2}(y-f)^2$
Absolute Loss $(L_1)$
$\Psi(y,f)_{L_1} = \vert y-f \vert$
Huber Loss
\(\Psi(y,f)_{\text{Huber},\delta} = \begin{cases}\begin{aligned} &\frac{1}{2}(y-f)^2 &\vert y-f \vert \leq \delta \\ &\delta(\vert y-f \vert - \delta/2) &\vert y-f \vert > \delta \end{aligned}\end{cases}\)
Quantile Loss
\(\Psi(y,f)_{\alpha} = \begin{cases}\begin{aligned} &(1-\alpha)\vert y-f \vert & y-f \leq 0 \\ &\alpha \vert y-f \vert & y-f > 0 \end{aligned}\end{cases}\)
Huber 오차에서의 $\delta$ 와 Quantile 오차에서의 $\alpha$ 는 하이퍼파라미터로서 어떤 값을 지정하는지에 따라서 생성되는 함수의 개형이 달라집니다. 아래는 각 손실 함수의 개형과 싱크 함수(sinc function) 1에 노이즈를 추가하여 생성한 데이터셋에 각 손실함수에 따라 생성되는 최종 함수를 비교한 결과입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
Classification
분류를 위한 손실 함수는 베르누이 오차, Adaboost 오차 등이 있습니다. 각각의 식은 아래와 같습니다. Adaboost와 마찬가지로 이진 분류시에 $y$ 의 레이블은 ${-1, 1}$ 로 합니다.
Loss Function
Formula
Bernoulli Loss
$\Psi(y,f)_\text{Bern} = \log(1+\exp(-2\bar{y}f))$
Absolute Loss
$\Psi(y,f)_\text{Ada} = \exp(-\bar{y}f)$
아래는 두 손실 함수의 개형을 나타낸 그래프입니다. Adaboost 손실 함수가 베르누이 손실 함수보다 더 빠르게 감소하는 것을 알 수 있습니다.

Regularization
그래디언트 부스팅 머신은 과적합(Overfitting)에 대한 문제를 가지고 있습니다. 정답 레이블을 $y$, 우리가 최종적으로 근사하고자 하는 함수를 $F(x)$, 소음으로 인해 발생하는 오차를 $\epsilon$ 이라 하면 $y = F(x) + \epsilon$ 으로 나타낼 수 있는데요. 근사하는 목적은 $F(x)$ 인데 반복수가 많아지다 보면 $\epsilon$ 까지 잔차로 인식해서 근사해버리는 과적합 문제가 발생합니다. 그래디언트 부스팅 머신의 과적합을 방지하기 위해서 적용하는 정칙화(Regularization) 방법에 대해 알아보겠습니다.
Subsampling
첫 번째 방법은 서브 샘플링(Subsampling)입니다. 이는 원래 데이터셋의 일부만을 추출하는 방법인데요. 원래의 데이터셋을 $D_0$ 이라 하면 이 데이터셋으로 첫 번째 약한 모델 $f_0$ 을 근사하게 되는데요. 다음 약한 모델 $f_1, \cdots$ 을 근사하기 위한 $D_1, \cdots$ 는 $D_0$ 를 전부 사용하지 않고 일부를 추출하는 방법입니다. 추출 방법으로는 기본적으로 비복원 추출을 기반으로 하고 있지만 복원 추출을 사용하여도 상관은 없습니다.
Shrinkage
수축법(Shrinkage)은 뒤쪽에 생성되는 모델의 영향력을 줄여주는 방법입니다. 아래 식에 있는 $\lambda$ 는 새로 생성되는 알고리즘의 영향을 얼마나 할 것인지를 정하는 하이퍼파라미터입니다. 이 값을 조정하여 뒤쪽에 생성되는 모델의 영향력이 줄어들면 뒤쪽에 생성되는 함수가 $\epsilon$ 까지 과하게 근사하지 못하도록 할 수 있습니다.
\[\hat{f}_t \leftarrow \hat{f}_{t-1} + \color{red}{\lambda} \rho_t h(x, \theta_t)\]
Early stopping
조기 종료(Early stopping)는 일반적으로 많이 사용되는 과적합 방지 방법입니다. 학습 오차와 검증 오차를 비교한 뒤에 검증 오차가 줄어들다가 다시 커지게 되면 반복을 종료하여 모델이 학습 데이터에 과적합 되는 현상을 막습니다.
Variable importance
랜덤 포레스트와 마찬가지로 그래디언트 부스팅 머신에서도 변수의 중요도를 측정할 수 있습니다. 일단 하나의 의사 결정 나무 $T$ 에서 변수 $j$ 의 중요도는 해당 변수를 사용했을 때 얻어지는 정보 획득량(Information gain, IG)을 모두 더하여 측정합니다. 수식으로 나타내면 아래와 같습니다. 아래 식에서 $L$ 은 해당 트리의 리프 노드의 개수이며 분기(Split) 횟수는 리프 노드 개수보다 1개 적기 때문에 $i = 1, \cdots, L-1$ 이 됩니다. $\mathbf{1}(S_i = j)$ 은 지시 함수(Indicator function)로 뒤 조건이 일치할 때는 $1$, 그렇지 않을 때는 $0$의 값을 가집니다. 여기서는 $i$ 번째 분기에 사용된 변수 $S_i$ 가 $j$ 가 동일할 때에만 $1$ 의 값을 나타냅니다.
\[\text{Influence}_j(T) = \sum^{L-1}_{i=1} (IG_i \times \mathbf{1}(S_i = j))\]
그래디언트 부스팅 머신에서 변수의 중요도는 각 트리마다 변수 $j$ 의 중요도를 평균내어 구합니다.
\[\text{Influence}_j = \frac{1}{M}\sum^{M}_{k=1} \text{Influence}_j(T_k)\]
Conclusion
Adaboost에 이은 새로운 부스팅 알고리즘인 그래디언트 부스팅 머신에 대해서 알아보았습니다. 그래디언트 부스팅 머신은 보다 좋은 성능을 보이지만 계속해서 근사 함수를 만들어 내야 하기 때문에 실행 시간이 오래 걸리고 많은 컴퓨팅 자원이 필요하다는 단점을 가지고 있습니다. 그래서 이후로 단점을 해결하기 위한 알고리즘이 계속해서 고안되었는데요. 다음에는 이를 개선한 XGBoost, LightGBM, CatBoost 등에 대해 알아보도록 하겠습니다.
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
Gradient Boosting Machine
이번에 알아볼 그래디언트 부스팅 머신(Gradient Boosting Machine, GBM)은 경사 하강법(Gradient descent)을 결합한 새로운 부스팅(Boosting) 알고리즘입니다. Adaboost는 이전 약한 모델의 오답에 가중치를 부여하여 새로운 모델을 학습하는 방법이었는데요. 그래디언트 부스팅 머신은 잔차(Residual)에 집중합니다. 이 잔차를 최소화하는 과정에서 경사 하강법을 사용하기 때문에 이런 이름이 붙었습니다.
Residual
그래디언트 부스팅 머신이 작동되는 방식에 대해서 알아보겠습니다. 먼저 첫 번째 약한 모델(Weak Model) $f_1(\mathbf{x})$ 를 만듭니다. 다음으로 정답과 예측값의 차이, 즉 잔차 $R_1$ 을 계산합니다.
\[y = f_1(\mathbf{x}) + R_1 \\ R_1 = y - f_1(\mathbf{x})\]다음으로는 잔차 $R_1$ 을 예측하는 두 번째 약한 모델 $f_2(\mathbf{x})$ 을 만듭니다. 그리고 $R_1$ 과 $f_2(\mathbf{x})$ 의 잔차 $R_2$ 를 구합니다.
\[R_1 = f_2(\mathbf{x}) + R_2 \\ R_2 = R_1 - f_2(\mathbf{x})\]이렇게 $t$ 번째 약한 모델 $f_t(\mathbf{x})$ 는 $t-1$ 번째의 잔차를 근사하는 함수입니다. 이를 $T$ 번 반복한 뒤 정리하면 다음과 같은 식이 될 것입니다. 첫 $R_1$ 은 꽤 크지만 이를 반복해서 근사하는 모델을 더해나가면 마지막 잔차 $R_T$ 는 매우 작아집니다.
\[y = f_1(\mathbf{x}) + f_2(\mathbf{x}) + \cdots + f_T(\mathbf{x}) + R_{T}\]만약 오차로 평균 제곱 오차(Mean square error, MSE)를 사용하는 회귀 문제라면 아래 이미지와 같이 생각해 볼 수도 있겠습니다.

이미지 출처 : github.com/topics/gradient-boosting-machine
반복 과정동안 잔차를 줄이는 것이 목적이므로 경사 하강법을 사용하여 잔차를 반복해서 줄여나갑니다. 아래는 Stump Tree를 약한 모델로 하는 그래디언트 부스팅 머신으로 회귀 함수를 근사하는 예시입니다. 아래는 1~3회 반복했을 때의 근사 함수와 잔차를 나타낸 이미지입니다.

이미지 출처 : medium.com/mlreview
낮은 반복수에서는 잔차가 꽤 크게 나오고 있습니다. 동일한 반복을 계속하면 함수 개형과 잔차가 어떻게 변하는 지 알아보겠습니다. 아래는 18~20회 반복했을 때의 근사 함수와 잔차를 나타낸 이미지입니다.

이미지 출처 : medium.com/mlreview
이전보다 잔차가 훨씬 더 줄어든 것을 볼 수 있습니다. 자세히 보면 함수도 좀 더 구불구불해진 것도 볼 수 있습니다. 동일한 과정을 50번 반복하면 아래와 같이 잔차가 더 줄어들고 함수도 더 복잡해집니다.

이미지 출처 : medium.com/mlreview
Loss Function
손실 함수(Loss function)의 기울기를 최소화하는 방향으로 추가적인 모델이 순차적으로 생성되기 때문에 어떤 손실 함수를 사용하는 지에 따라 최종으로 생성되는 함수가 달라집니다. 크게는 풀고자하는 문제가 회귀인지 분류인지에 따라서 다른 선택지를 갖게 됩니다.
Regression
회귀를 위한 손실 함수는 제곱 오차, 절대 오차, Huber 오차, Quantile 오차 등이 있습니다. 각각의 식은 아래와 같으며 일반적으로는 제곱 오차 $(L_2)$ 를 많이 사용합니다.
| Loss Function | Formula |
|---|---|
| Squared Loss $(L_2)$ | $\Psi(y,f)_{L_2} = \frac{1}{2}(y-f)^2$ |
| Absolute Loss $(L_1)$ | $\Psi(y,f)_{L_1} = \vert y-f \vert$ |
| Huber Loss | \(\Psi(y,f)_{\text{Huber},\delta} = \begin{cases}\begin{aligned} &\frac{1}{2}(y-f)^2 &\vert y-f \vert \leq \delta \\ &\delta(\vert y-f \vert - \delta/2) &\vert y-f \vert > \delta \end{aligned}\end{cases}\) |
| Quantile Loss | \(\Psi(y,f)_{\alpha} = \begin{cases}\begin{aligned} &(1-\alpha)\vert y-f \vert & y-f \leq 0 \\ &\alpha \vert y-f \vert & y-f > 0 \end{aligned}\end{cases}\) |
Huber 오차에서의 $\delta$ 와 Quantile 오차에서의 $\alpha$ 는 하이퍼파라미터로서 어떤 값을 지정하는지에 따라서 생성되는 함수의 개형이 달라집니다. 아래는 각 손실 함수의 개형과 싱크 함수(sinc function) 1에 노이즈를 추가하여 생성한 데이터셋에 각 손실함수에 따라 생성되는 최종 함수를 비교한 결과입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
Classification
분류를 위한 손실 함수는 베르누이 오차, Adaboost 오차 등이 있습니다. 각각의 식은 아래와 같습니다. Adaboost와 마찬가지로 이진 분류시에 $y$ 의 레이블은 ${-1, 1}$ 로 합니다.
| Loss Function | Formula |
|---|---|
| Bernoulli Loss | $\Psi(y,f)_\text{Bern} = \log(1+\exp(-2\bar{y}f))$ |
| Absolute Loss | $\Psi(y,f)_\text{Ada} = \exp(-\bar{y}f)$ |
아래는 두 손실 함수의 개형을 나타낸 그래프입니다. Adaboost 손실 함수가 베르누이 손실 함수보다 더 빠르게 감소하는 것을 알 수 있습니다.

Regularization
그래디언트 부스팅 머신은 과적합(Overfitting)에 대한 문제를 가지고 있습니다. 정답 레이블을 $y$, 우리가 최종적으로 근사하고자 하는 함수를 $F(x)$, 소음으로 인해 발생하는 오차를 $\epsilon$ 이라 하면 $y = F(x) + \epsilon$ 으로 나타낼 수 있는데요. 근사하는 목적은 $F(x)$ 인데 반복수가 많아지다 보면 $\epsilon$ 까지 잔차로 인식해서 근사해버리는 과적합 문제가 발생합니다. 그래디언트 부스팅 머신의 과적합을 방지하기 위해서 적용하는 정칙화(Regularization) 방법에 대해 알아보겠습니다.
Subsampling
첫 번째 방법은 서브 샘플링(Subsampling)입니다. 이는 원래 데이터셋의 일부만을 추출하는 방법인데요. 원래의 데이터셋을 $D_0$ 이라 하면 이 데이터셋으로 첫 번째 약한 모델 $f_0$ 을 근사하게 되는데요. 다음 약한 모델 $f_1, \cdots$ 을 근사하기 위한 $D_1, \cdots$ 는 $D_0$ 를 전부 사용하지 않고 일부를 추출하는 방법입니다. 추출 방법으로는 기본적으로 비복원 추출을 기반으로 하고 있지만 복원 추출을 사용하여도 상관은 없습니다.
Shrinkage
수축법(Shrinkage)은 뒤쪽에 생성되는 모델의 영향력을 줄여주는 방법입니다. 아래 식에 있는 $\lambda$ 는 새로 생성되는 알고리즘의 영향을 얼마나 할 것인지를 정하는 하이퍼파라미터입니다. 이 값을 조정하여 뒤쪽에 생성되는 모델의 영향력이 줄어들면 뒤쪽에 생성되는 함수가 $\epsilon$ 까지 과하게 근사하지 못하도록 할 수 있습니다.
\[\hat{f}_t \leftarrow \hat{f}_{t-1} + \color{red}{\lambda} \rho_t h(x, \theta_t)\]Early stopping
조기 종료(Early stopping)는 일반적으로 많이 사용되는 과적합 방지 방법입니다. 학습 오차와 검증 오차를 비교한 뒤에 검증 오차가 줄어들다가 다시 커지게 되면 반복을 종료하여 모델이 학습 데이터에 과적합 되는 현상을 막습니다.
Variable importance
랜덤 포레스트와 마찬가지로 그래디언트 부스팅 머신에서도 변수의 중요도를 측정할 수 있습니다. 일단 하나의 의사 결정 나무 $T$ 에서 변수 $j$ 의 중요도는 해당 변수를 사용했을 때 얻어지는 정보 획득량(Information gain, IG)을 모두 더하여 측정합니다. 수식으로 나타내면 아래와 같습니다. 아래 식에서 $L$ 은 해당 트리의 리프 노드의 개수이며 분기(Split) 횟수는 리프 노드 개수보다 1개 적기 때문에 $i = 1, \cdots, L-1$ 이 됩니다. $\mathbf{1}(S_i = j)$ 은 지시 함수(Indicator function)로 뒤 조건이 일치할 때는 $1$, 그렇지 않을 때는 $0$의 값을 가집니다. 여기서는 $i$ 번째 분기에 사용된 변수 $S_i$ 가 $j$ 가 동일할 때에만 $1$ 의 값을 나타냅니다.
\[\text{Influence}_j(T) = \sum^{L-1}_{i=1} (IG_i \times \mathbf{1}(S_i = j))\]그래디언트 부스팅 머신에서 변수의 중요도는 각 트리마다 변수 $j$ 의 중요도를 평균내어 구합니다.
\[\text{Influence}_j = \frac{1}{M}\sum^{M}_{k=1} \text{Influence}_j(T_k)\]Conclusion
Adaboost에 이은 새로운 부스팅 알고리즘인 그래디언트 부스팅 머신에 대해서 알아보았습니다. 그래디언트 부스팅 머신은 보다 좋은 성능을 보이지만 계속해서 근사 함수를 만들어 내야 하기 때문에 실행 시간이 오래 걸리고 많은 컴퓨팅 자원이 필요하다는 단점을 가지고 있습니다. 그래서 이후로 단점을 해결하기 위한 알고리즘이 계속해서 고안되었는데요. 다음에는 이를 개선한 XGBoost, LightGBM, CatBoost 등에 대해 알아보도록 하겠습니다.

Comments