앙상블(Ensemble)
18 Mar 2021 | Machine-Learning
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
Ensemble
이번 게시물에서는 앙상블(Ensemble)에 대해서 알아보도록 하겠습니다. 앙상블이란 무엇일까요? 위키피디아가 말하는 앙상블의 정의는 다음과 같습니다.
앙상블(프랑스어: ensemble)은 전체적인 어울림이나 통일. ‘조화’로 순화한다는 의미의 프랑스어이며 음악에서 2인 이상이 하는 노래나 연주를 말하며 흔히 뮤지컬에서 주, 조연 배우들 뒤에서 화음을 넣으며 춤을 추고 노래를 부르면서 분위기를 돋구는 역할을 말한다.
‘조화로 순화한다’ 라는 문구가 눈에 띄는데요. 머신러닝에서의 앙상블 역시 이런 역할을 합니다. 더 좋은 성능을 내기 위해서 2개 이상의 모델을 잘 조합하지요. 모델 하나 공부하기도 어려운데 2개 이상의 모델을 서로 엮다니… 이런 기이한 짓(?)을 왜 하는지에 대해서 알아보도록 하겠습니다.
No Free Lunch Theorem
“공짜 점심은 없다!(There ain’t no such thing as a free lunch!)”라는 말은 경제학자인 밀턴 프리드먼이 인용하여 유명해졌는데요. 경제학에서는 기회비용을 무시하지 말라는 뜻으로 사용되었습니다. 머신러닝에서도 해당 문장의 일부를 인용하여 『No Free Lunch Theorems for Optimization』1 이라는 논문을 발표하였습니다. 논문의 요지는 머신러닝에도 “모든 문제에 대하여 다른 모델보다 항상 우월한 모델은 없다는 공짜점심없음 이론(NFL Theorem)이 있다”입니다. 다시 말해 ‘좋은 모델’의 기준은 주어지는 문제에 따라 달라진다는 것이지요.
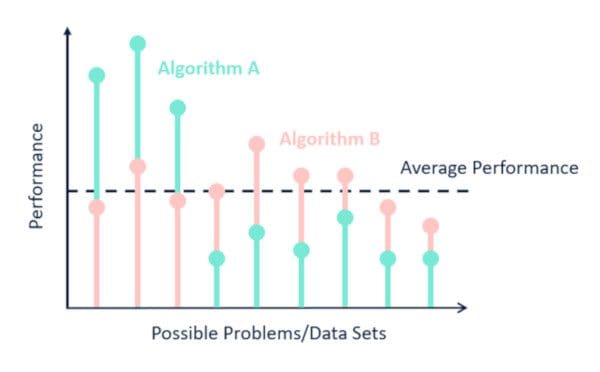
이미지 출처 : www.kdnuggets.com
평균 성능이 동일한 두 알고리즘(A, B)이라도 어떤 데이터셋이 주어지느냐에 따라서 성능이 많이 달라집니다. 앞의 세 가지 데이터셋에 대해서는 A의 성능이 월등히 높지만 나머지에 대해서는 B의 성능이 더 좋습니다. 어떤 알고리즘이 “일반적으로 더 우월하다”고 말할 수 없지요. 단지 주어진 데이터셋의 패턴을 잘 인식한 알고리즘이 성능이 잘 나올 뿐입니다.
Power of Ensemble
공짜 점심은 없으니 단일 알고리즘 대신 “여러 모델을 적절히 조합하면 데이터셋의 다양한 패턴을 적절히 인식할 수 있지 않을까?”라는 아이디어에서 앙상블이 시작되었습니다. 단순한 아이디어였지만 앙상블의 힘은 대단했습니다. (효과는 굉장했다!!)
표 형태의(Tabular) 데이터뿐만 아니라 이미지나 자연어 데이터에서도 앙상블 모델이 상위권을 차지하고 있지요. 이미지 데이터셋에 대해 객체 인식 등의 태스크 성능을 경쟁하는 ILSVRC라는 대회가 있는데요. 16~17년도 리더보드 상위권에 수많은 앙상블 모델이 자리잡고 있습니다. 질의 응답의 성능을 비교하는 대표적인 데이터셋 SQuAD의 상위권은 전부 앙상블 모델입니다.

이미지 출처 : rajpurkar.github.io/SQuAD-explorer
2016년, 대표적인 머신러닝 컨퍼런스인 MLconf에서는 10가지 요점 중 하나로 “앙상블은 거의 항상 (싱글 모델보다) 잘 작동한다.(Ensembles almost always work better)”를 꼽기도 했습니다. 그렇다면 앙상블이 이렇게 좋은 성능을 보이는 이유는 무엇일까요?
Why Ensemble?
앙상블이 (하나의 단일 모델보다) 잘 작동하는 이유에 대해서 알기 위해서는 ‘편향-분산 (오차)분해 (Bias-Variance Decomposition)’라는 개념을 알고 있어야 합니다. 해당 내용은 이곳에서 다룬 적이 있는데요. 해당 식을 다시 가지고 와보겠습니다.
Bias-Variance Decomposition
먼저 앞으로 나올 여러 기호에 대한 설명을 하고 넘어가겠습니다. $F^*(\mathbf{x})$ 는 정답 모델에 해당하는 함수입니다. 우리가 알고자 하는 함수라고도 할 수 있지요. $\epsilon$ 은 현실적으로 발생하는 소음(Noise)이며 이 값은 동일하고 독립인 분포(i.i.d) $N(0, \sigma^2)$ 를 따른다고 가정하겠습니다. 특정 데이터셋으로부터 추정한 모델의 함수를 $\hat{F_D}(\mathbf{x})$ 라 하고 모든 데이터셋에 대해 이를 평균낸 값을 $\bar{F}(\mathbf{x})$ 라고 하겠습니다. 위 함수들의 관계를 아래와 같이 나타낼 수 있습니다.
\[y = F^*(\mathbf{x})+\epsilon, \quad \epsilon \sim N(0,\sigma^2) \\
\bar{F}(\mathbf{x}) = E[\hat{F_D}(\mathbf{x})]\]
특정 데이터 $\mathbf{x}_0$ 에 대한 오차를 다음과 같이 구할 수 있습니다.
\[\begin{aligned}
\text{Error}(\mathbf{x}_0) &= E\big[(y - \hat{F}(\mathbf{x}) \vert \mathbf{x} = \mathbf{x}_0)^2 \big] \\
&= E\big[(F^*(\mathbf{x})+\epsilon - \hat{F}(\mathbf{x}))^2 \big] \qquad (\because y = F^*(\mathbf{x})+\epsilon) \\
&= E\big[(F^*(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 \big] + \sigma^2 \\
&= E\big[(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}) + \bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 \big] + \sigma^2 \\
&= E\big[(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}))^2 + (\bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 + 2(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}))(\bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x})) \big] + \sigma^2 \\
&= \color{blue}{E\big[(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}))^2\big]} + \color{red}{E\big[(\bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 \big]} + \sigma^2 \\
&= \color{blue}{\text{Bias}^2(\hat{F}(\mathbf{x}_0))} + \color{red}{\text{Var}^2(\hat{F}(\mathbf{x}_0))} + \sigma^2
\end{aligned}\]
특정 데이터로부터의 에러를 편향과 분산에 의한 에러로 나눠볼 수 있습니다. 편향은 $E\big[(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}))^2\big]$ 에 해당합니다. 정답과 평균 추정치가 얼마나 차이나는 지를 나타내지요. 편향이 높으면 과소적합(Underfitting)이 발생합니다. 분산은 $E\big[(\bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 \big]$ 에 해당합니다. 평균 추정치와 특정 데이터셋에 대한 추정치가 얼마나 차이나는 지를 나타냅니다. 분산이 높으면 과적합(Overfitting)이 발생합니다.
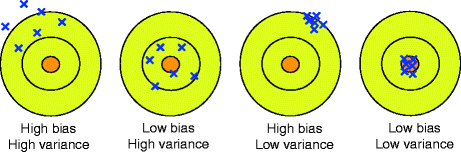
위 그림은 편향이 높고 낮은 경우와 분산이 높고 낮은 각각의 경우를 도식화하여 보여주고 있습니다. 분산만 높은 경우 어떤 데이터에는 잘 맞지만, 어떤 데이터에는 잘 맞지 않습니다. 편향만 높은 경우 전체적으로 잘 맞지 않지만 데이터별 차이는 그리 크지 않음을 확인할 수 있습니다.
일반적으로 모델의 복잡도(Complexity)가 작으면 분산이 낮고 편향이 높습니다.(3번째 그림) 이런 모델로는 로지스틱 회귀(Logistic Regression), 선형 판별 분석(FLDA), k가 클 때의 k-NN(k-최근접이웃) 등이 있습니다. 반대로 복잡도가 높으면 분산이 높고 편향이 낮습니다.(2번째 그림) 이런 모델로는 (Pruning을 해주지 않은) 의사결정나무, 인공신경망, 서포트 벡터 머신, k가 작을 때의 k-NN 등이 있습니다.
with Ensemble
단일 모델이 2번 혹은 3번 그림이라면 앙상블은 이 모델을 4번으로 만들기 위해 사용합니다. 앙상블의 목적은 각 단일 모델의 좋은 성능을 유지하면서도 다양성을 확보하는 데에 있습니다. 전체 데이터셋의 부분집합에 해당하는 여러 데이터셋을 준비한 뒤에 각각을 따로 학습시키면 Implicit diversity를 확보할 수 있습니다. 이 방법과는 조금 다르게 먼저 생성된 모델의 측정값으로부터 새로운 모델을 생성하면 Explicit diversity를 확보할 수 있지요.
전자에 해당하는 방법은 분산을 줄일 수 있으며 배깅(Bagging)이나 랜덤 포레스트(Random Forest) 등이 있습니다. 후자에 해당하는 방법은 편향을 줄일 수 있으며 부스팅(Boosting)이나 NCL(Negative correlation learning) 등이 있습니다. 아래는 전자(왼쪽)과 후자(오른쪽) 모델이 생성되는 방식을 나타낸 이미지입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
왼쪽에 해당하는 모델은 여러 데이터셋을 준비한 뒤에 각각의 모델을 병렬적으로 학습합니다. 오른쪽에 해당하는 모델은 첫 번째 모델이 얻어내는 어떤 정보를 바탕으로 두 번째 모델을 생성합니다. 이렇게 여러 개의 모델을 순차적으로 학습하게 됩니다.
앙상블 방법의 오차는 얼마나 될까요? $M$ 개의 모델을 엮은 앙상블 모델이 있다고 해보겠습니다. $m$ 번째 모델에 대해 정답과 오차의 관계를 다음과 같이 나타낼 수 있습니다.
\[\begin{aligned}
&y_m(\mathbf{x}) = f(\mathbf{x}) + \epsilon_m(\mathbf{x}). \\
&\mathbb{E}_\mathbf{x}[\{y_m(\mathbf{x}) - f(\mathbf{x})\}^2] = \mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})^2]
\end{aligned}\]
이를 활용하여 각 모델의 오차 평균과 앙상블 모델의 오차를 구하면 다음과 같습니다.
\[\begin{aligned}
E_\text{Avg} &= \frac{1}{M} \sum_{i=1}^M \mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})^2] \\
E_\text{Ensemble} &= \mathbb{E}_\mathbf{x}\bigg[\big\{\frac{1}{M}\sum_{i=1}^My_m(\mathbf{x}) - f(x)\big\}^2\bigg] \\
&= \mathbb{E}_\mathbf{x}\bigg[\big\{\frac{1}{M}\sum_{i=1}^M\epsilon_m(\mathbf{x})\big\}^2\bigg]
\end{aligned}\]
만약 모델의 $\epsilon$ 평균이 0이라고 가정하면 방정식 $\mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})] = 0$ 을 만족합니다. 그리고 앙상블에 사용된 각각의 모델이 연관되어 있지 않는 가정하에서는 아래의 방정식을 만족합니다.
\[\mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})\epsilon_l(\mathbf{x})] = 0 \quad (m \neq l)\]
이 두 가지 가정하에서, 앙상블 모델은 각 모델의 평균의 $1/M$ 의 오차를 갖게 됩니다.
\[E_\text{Ensemble} = \frac{1}{M} E_\text{Avg}\]
하지만 위 가정은 현실에서는 거의 불가능합니다. 앙상블 오차의 상한은 코시-슈바르츠 부등식2을 사용하여 구할 수 있습니다. 코시-슈바르츠 부등식은 다음과 같습니다.
\[(a^2+b^2)(x^2+y^2) \geq (ax + by)^2\]
이를 일반화하여 각 모델의 오차에 적용하면 다음과 같은 식을 만들 수 있습니다.
\[\begin{aligned}
M\sum_{i=1}^M \mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})^2] &\geq \bigg[\sum_{i=1}^M \mathbb{E}_\mathbf{x}\epsilon_m(\mathbf{x}) \bigg]^2 \\
\frac{1}{M}\sum_{i=1}^M \mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})^2] &\geq \bigg[\frac{1}{M}\sum_{i=1}^M \mathbb{E}_\mathbf{x}\epsilon_m(\mathbf{x}) \bigg]^2 \\
E_\text{Avg} &\geq E_\text{Ensemble}
\end{aligned}\]
앙상블의 오차는 무조건 앙상블을 구성하는 모델 오차의 평균보다는 작음을 알 수 있습니다. 또한 경험적으로는 대개 최고 성능을 보이는 개별 모델보다도 낮은 오차를 보인다고 합니다. 이런 이유에서 앙상블은 모델의 성능을 높이기 위해서 자주 사용되며, 실제로도 최고의 성능을 기록하고 있습니다. 이후 게시물에서는 다양한 앙상블 방법에 대해서 알아보도록 하겠습니다.
-
David H. Wolpert and William G. Macready, No Free Lunch Theorems for Optimization, IEEE Transactions on Evolutionary Computation (Volume: 1, Issue: 1, Apr 1997) ↩
-
위키피디아 : 코시-슈바르츠 부등식 ↩
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
Ensemble
이번 게시물에서는 앙상블(Ensemble)에 대해서 알아보도록 하겠습니다. 앙상블이란 무엇일까요? 위키피디아가 말하는 앙상블의 정의는 다음과 같습니다.
앙상블(프랑스어: ensemble)은 전체적인 어울림이나 통일. ‘조화’로 순화한다는 의미의 프랑스어이며 음악에서 2인 이상이 하는 노래나 연주를 말하며 흔히 뮤지컬에서 주, 조연 배우들 뒤에서 화음을 넣으며 춤을 추고 노래를 부르면서 분위기를 돋구는 역할을 말한다.
‘조화로 순화한다’ 라는 문구가 눈에 띄는데요. 머신러닝에서의 앙상블 역시 이런 역할을 합니다. 더 좋은 성능을 내기 위해서 2개 이상의 모델을 잘 조합하지요. 모델 하나 공부하기도 어려운데 2개 이상의 모델을 서로 엮다니… 이런 기이한 짓(?)을 왜 하는지에 대해서 알아보도록 하겠습니다.
No Free Lunch Theorem
“공짜 점심은 없다!(There ain’t no such thing as a free lunch!)”라는 말은 경제학자인 밀턴 프리드먼이 인용하여 유명해졌는데요. 경제학에서는 기회비용을 무시하지 말라는 뜻으로 사용되었습니다. 머신러닝에서도 해당 문장의 일부를 인용하여 『No Free Lunch Theorems for Optimization』1 이라는 논문을 발표하였습니다. 논문의 요지는 머신러닝에도 “모든 문제에 대하여 다른 모델보다 항상 우월한 모델은 없다는 공짜점심없음 이론(NFL Theorem)이 있다”입니다. 다시 말해 ‘좋은 모델’의 기준은 주어지는 문제에 따라 달라진다는 것이지요.

이미지 출처 : www.kdnuggets.com
평균 성능이 동일한 두 알고리즘(A, B)이라도 어떤 데이터셋이 주어지느냐에 따라서 성능이 많이 달라집니다. 앞의 세 가지 데이터셋에 대해서는 A의 성능이 월등히 높지만 나머지에 대해서는 B의 성능이 더 좋습니다. 어떤 알고리즘이 “일반적으로 더 우월하다”고 말할 수 없지요. 단지 주어진 데이터셋의 패턴을 잘 인식한 알고리즘이 성능이 잘 나올 뿐입니다.
Power of Ensemble
공짜 점심은 없으니 단일 알고리즘 대신 “여러 모델을 적절히 조합하면 데이터셋의 다양한 패턴을 적절히 인식할 수 있지 않을까?”라는 아이디어에서 앙상블이 시작되었습니다. 단순한 아이디어였지만 앙상블의 힘은 대단했습니다. (효과는 굉장했다!!)
표 형태의(Tabular) 데이터뿐만 아니라 이미지나 자연어 데이터에서도 앙상블 모델이 상위권을 차지하고 있지요. 이미지 데이터셋에 대해 객체 인식 등의 태스크 성능을 경쟁하는 ILSVRC라는 대회가 있는데요. 16~17년도 리더보드 상위권에 수많은 앙상블 모델이 자리잡고 있습니다. 질의 응답의 성능을 비교하는 대표적인 데이터셋 SQuAD의 상위권은 전부 앙상블 모델입니다.

이미지 출처 : rajpurkar.github.io/SQuAD-explorer
2016년, 대표적인 머신러닝 컨퍼런스인 MLconf에서는 10가지 요점 중 하나로 “앙상블은 거의 항상 (싱글 모델보다) 잘 작동한다.(Ensembles almost always work better)”를 꼽기도 했습니다. 그렇다면 앙상블이 이렇게 좋은 성능을 보이는 이유는 무엇일까요?
Why Ensemble?
앙상블이 (하나의 단일 모델보다) 잘 작동하는 이유에 대해서 알기 위해서는 ‘편향-분산 (오차)분해 (Bias-Variance Decomposition)’라는 개념을 알고 있어야 합니다. 해당 내용은 이곳에서 다룬 적이 있는데요. 해당 식을 다시 가지고 와보겠습니다.
Bias-Variance Decomposition
먼저 앞으로 나올 여러 기호에 대한 설명을 하고 넘어가겠습니다. $F^*(\mathbf{x})$ 는 정답 모델에 해당하는 함수입니다. 우리가 알고자 하는 함수라고도 할 수 있지요. $\epsilon$ 은 현실적으로 발생하는 소음(Noise)이며 이 값은 동일하고 독립인 분포(i.i.d) $N(0, \sigma^2)$ 를 따른다고 가정하겠습니다. 특정 데이터셋으로부터 추정한 모델의 함수를 $\hat{F_D}(\mathbf{x})$ 라 하고 모든 데이터셋에 대해 이를 평균낸 값을 $\bar{F}(\mathbf{x})$ 라고 하겠습니다. 위 함수들의 관계를 아래와 같이 나타낼 수 있습니다.
\[y = F^*(\mathbf{x})+\epsilon, \quad \epsilon \sim N(0,\sigma^2) \\ \bar{F}(\mathbf{x}) = E[\hat{F_D}(\mathbf{x})]\]특정 데이터 $\mathbf{x}_0$ 에 대한 오차를 다음과 같이 구할 수 있습니다.
\[\begin{aligned} \text{Error}(\mathbf{x}_0) &= E\big[(y - \hat{F}(\mathbf{x}) \vert \mathbf{x} = \mathbf{x}_0)^2 \big] \\ &= E\big[(F^*(\mathbf{x})+\epsilon - \hat{F}(\mathbf{x}))^2 \big] \qquad (\because y = F^*(\mathbf{x})+\epsilon) \\ &= E\big[(F^*(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 \big] + \sigma^2 \\ &= E\big[(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}) + \bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 \big] + \sigma^2 \\ &= E\big[(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}))^2 + (\bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 + 2(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}))(\bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x})) \big] + \sigma^2 \\ &= \color{blue}{E\big[(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}))^2\big]} + \color{red}{E\big[(\bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 \big]} + \sigma^2 \\ &= \color{blue}{\text{Bias}^2(\hat{F}(\mathbf{x}_0))} + \color{red}{\text{Var}^2(\hat{F}(\mathbf{x}_0))} + \sigma^2 \end{aligned}\]특정 데이터로부터의 에러를 편향과 분산에 의한 에러로 나눠볼 수 있습니다. 편향은 $E\big[(F^*(\mathbf{x}) - \bar{F}(\mathbf{x}))^2\big]$ 에 해당합니다. 정답과 평균 추정치가 얼마나 차이나는 지를 나타내지요. 편향이 높으면 과소적합(Underfitting)이 발생합니다. 분산은 $E\big[(\bar{F}(\mathbf{x}) - \hat{F}(\mathbf{x}))^2 \big]$ 에 해당합니다. 평균 추정치와 특정 데이터셋에 대한 추정치가 얼마나 차이나는 지를 나타냅니다. 분산이 높으면 과적합(Overfitting)이 발생합니다.

위 그림은 편향이 높고 낮은 경우와 분산이 높고 낮은 각각의 경우를 도식화하여 보여주고 있습니다. 분산만 높은 경우 어떤 데이터에는 잘 맞지만, 어떤 데이터에는 잘 맞지 않습니다. 편향만 높은 경우 전체적으로 잘 맞지 않지만 데이터별 차이는 그리 크지 않음을 확인할 수 있습니다.
일반적으로 모델의 복잡도(Complexity)가 작으면 분산이 낮고 편향이 높습니다.(3번째 그림) 이런 모델로는 로지스틱 회귀(Logistic Regression), 선형 판별 분석(FLDA), k가 클 때의 k-NN(k-최근접이웃) 등이 있습니다. 반대로 복잡도가 높으면 분산이 높고 편향이 낮습니다.(2번째 그림) 이런 모델로는 (Pruning을 해주지 않은) 의사결정나무, 인공신경망, 서포트 벡터 머신, k가 작을 때의 k-NN 등이 있습니다.
with Ensemble
단일 모델이 2번 혹은 3번 그림이라면 앙상블은 이 모델을 4번으로 만들기 위해 사용합니다. 앙상블의 목적은 각 단일 모델의 좋은 성능을 유지하면서도 다양성을 확보하는 데에 있습니다. 전체 데이터셋의 부분집합에 해당하는 여러 데이터셋을 준비한 뒤에 각각을 따로 학습시키면 Implicit diversity를 확보할 수 있습니다. 이 방법과는 조금 다르게 먼저 생성된 모델의 측정값으로부터 새로운 모델을 생성하면 Explicit diversity를 확보할 수 있지요.
전자에 해당하는 방법은 분산을 줄일 수 있으며 배깅(Bagging)이나 랜덤 포레스트(Random Forest) 등이 있습니다. 후자에 해당하는 방법은 편향을 줄일 수 있으며 부스팅(Boosting)이나 NCL(Negative correlation learning) 등이 있습니다. 아래는 전자(왼쪽)과 후자(오른쪽) 모델이 생성되는 방식을 나타낸 이미지입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654
왼쪽에 해당하는 모델은 여러 데이터셋을 준비한 뒤에 각각의 모델을 병렬적으로 학습합니다. 오른쪽에 해당하는 모델은 첫 번째 모델이 얻어내는 어떤 정보를 바탕으로 두 번째 모델을 생성합니다. 이렇게 여러 개의 모델을 순차적으로 학습하게 됩니다.
앙상블 방법의 오차는 얼마나 될까요? $M$ 개의 모델을 엮은 앙상블 모델이 있다고 해보겠습니다. $m$ 번째 모델에 대해 정답과 오차의 관계를 다음과 같이 나타낼 수 있습니다.
\[\begin{aligned} &y_m(\mathbf{x}) = f(\mathbf{x}) + \epsilon_m(\mathbf{x}). \\ &\mathbb{E}_\mathbf{x}[\{y_m(\mathbf{x}) - f(\mathbf{x})\}^2] = \mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})^2] \end{aligned}\]이를 활용하여 각 모델의 오차 평균과 앙상블 모델의 오차를 구하면 다음과 같습니다.
\[\begin{aligned} E_\text{Avg} &= \frac{1}{M} \sum_{i=1}^M \mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})^2] \\ E_\text{Ensemble} &= \mathbb{E}_\mathbf{x}\bigg[\big\{\frac{1}{M}\sum_{i=1}^My_m(\mathbf{x}) - f(x)\big\}^2\bigg] \\ &= \mathbb{E}_\mathbf{x}\bigg[\big\{\frac{1}{M}\sum_{i=1}^M\epsilon_m(\mathbf{x})\big\}^2\bigg] \end{aligned}\]만약 모델의 $\epsilon$ 평균이 0이라고 가정하면 방정식 $\mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})] = 0$ 을 만족합니다. 그리고 앙상블에 사용된 각각의 모델이 연관되어 있지 않는 가정하에서는 아래의 방정식을 만족합니다.
\[\mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})\epsilon_l(\mathbf{x})] = 0 \quad (m \neq l)\]이 두 가지 가정하에서, 앙상블 모델은 각 모델의 평균의 $1/M$ 의 오차를 갖게 됩니다.
\[E_\text{Ensemble} = \frac{1}{M} E_\text{Avg}\]하지만 위 가정은 현실에서는 거의 불가능합니다. 앙상블 오차의 상한은 코시-슈바르츠 부등식2을 사용하여 구할 수 있습니다. 코시-슈바르츠 부등식은 다음과 같습니다.
\[(a^2+b^2)(x^2+y^2) \geq (ax + by)^2\]이를 일반화하여 각 모델의 오차에 적용하면 다음과 같은 식을 만들 수 있습니다.
\[\begin{aligned} M\sum_{i=1}^M \mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})^2] &\geq \bigg[\sum_{i=1}^M \mathbb{E}_\mathbf{x}\epsilon_m(\mathbf{x}) \bigg]^2 \\ \frac{1}{M}\sum_{i=1}^M \mathbb{E}_\mathbf{x}[\epsilon_m(\mathbf{x})^2] &\geq \bigg[\frac{1}{M}\sum_{i=1}^M \mathbb{E}_\mathbf{x}\epsilon_m(\mathbf{x}) \bigg]^2 \\ E_\text{Avg} &\geq E_\text{Ensemble} \end{aligned}\]앙상블의 오차는 무조건 앙상블을 구성하는 모델 오차의 평균보다는 작음을 알 수 있습니다. 또한 경험적으로는 대개 최고 성능을 보이는 개별 모델보다도 낮은 오차를 보인다고 합니다. 이런 이유에서 앙상블은 모델의 성능을 높이기 위해서 자주 사용되며, 실제로도 최고의 성능을 기록하고 있습니다. 이후 게시물에서는 다양한 앙상블 방법에 대해서 알아보도록 하겠습니다.
-
David H. Wolpert and William G. Macready, No Free Lunch Theorems for Optimization, IEEE Transactions on Evolutionary Computation (Volume: 1, Issue: 1, Apr 1997) ↩
-
위키피디아 : 코시-슈바르츠 부등식 ↩

Comments