로지스틱 회귀 (Logistic Regression)
19 Apr 2020 | Machine-Learning
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 강의를 바탕으로 작성하였습니다.
Logistic Regression
나이브 베이즈 분류기 에서는 최적의 분류기란 어떤 것인지에 대해 아래의 그림을 통해 알아보았습니다. 아래는 두 분류기의 확률 밀도 함수를 점선과 실선으로 각각 나타낸 것입니다.

이미지 출처 : 인공지능 및 기계학습 개론 학습자료
위 그림에서 베이즈 위험(Bayes’ risk)을 통해 점선보다 실선 분류기가 더 좋은 성능을 나타낼 것으로 판단하였습니다. 실선 분류기의 베이즈 위험이 더 작았기 때문입니다. 실선 분류기가 점선보다 베이즈 위험이 낮은 이유는 결정 경계(Decision boundary)에서 확률이 더욱 급격하게 변했기 때문입니다. 즉, 결정 경계에서 급하게 변할수록 더 좋은 분류기가 되는 것이지요.
이번 게시물에서 다루게 될 로지스틱 회귀는 결정 경계에서 확률이 급격하게 변하는 분류기 입니다. 로지스틱 회귀에서는 결정 경계에서 확률이 급격히 변하는 시그모이드 함수를 사용합니다. 시그모이드 함수란 무엇인지 알아봅시다.
Sigmoid
시그모이드 함수(Sigmoid function) 란 실수 정의역 범위에서 최댓값이 1이하이고 최솟값이 0이상인 미분가능한 단조증가함수입니다. 시그모이드 함수는 특정한 하나의 함수가 아니라 이런 조건을 만족하는 함수 집합입니다. $\tanh{x} , \arctan{x} , 1/(1+e^{-x})$ 등 다양한 형태의 시그모이드 함수가 있습니다. 이 중 세 번째에 있는 함수를 로지스틱 함수(Logistic function) 라고 합니다. 바로 이 로지스틱 함수를 사용한 회귀이기 때문에 로지스틱 회귀라는 이름이 붙은 것입니다.
로지스틱 함수를 사용하는 이유는 미분 계산이 쉽기 때문입니다. 일반적으로 분류기를 최적화(Optimization)하기 위해서는 특정 확률이 최대 혹은 최소가 되는 점을 찾습니다. 이러한 점을 찾는 데에 미분 계산은 필수적인 관문입니다. 로지스틱 함수는 이 미분 계산을 쉽게 만들어주기 때문에 데이터셋이 많아지더라도 수행 시간을 적절한 선에서 유지할 수 있다는 장점을 가지고 있습니다.
Logistic function
로지스틱 함수의 수식을 다시 써보겠습니다.
\[y = \frac{1}{1+e^{-x}}\]
로지스틱 함수의 형태가 위와 같이 된 이유는 무엇일까요? 시작은 오즈(Odds) 라는 개념에서부터 시작합니다. 오즈는 확률의 또 다른 표현법 중 하나입니다. 어떤 사건이 일어날 확률을 $x$ 라고 했을 때 오즈는 다음와 가같이 나타낼 수 있습니다.
\[\text{Odds} = \frac{x}{1-x}\]
오즈는 한 가지 단점을 가지고 있습니다. $x$ 가 커지는 경우에 대해서는 값이 양의 무한대로 증가하지만 $x$ 가 작아지는 경우에 대해서는 0이하로는 작아지지 않는다는 것이지요. $x = 0.5$ 일 때를 기준으로 $x = 0.99$ 로 매우 클 때와 $x = 0.01$ 로 매우 작을 때 오즈가 어떻게 변하는지 봅시다.
\[\begin{aligned}
\text{Odds}(x = 0.5) &= \frac{0.5}{1-0.5} = 1 \\
\text{Odds}(x = 0.99) &= \frac{0.99}{1-0.99} = 99 \\
\text{Odds}(x = 0.01) &= \frac{0.01}{1-0.01} = \frac{1}{99}
\end{aligned}\]
$x = 0.5$ 일 때, 즉 어떤 사건이 일어날 때와 일어나지 않을 때의 확률이 동일할 때의 확률은 $1$ 입니다. 이를 기준으로 $x > 0.5$ 인 방향으로 변하면 오즈가 급격하게 커지지만 $x < 0.5$ 인 방향으로 변할 때는 오즈가 완만하게 줄어드는 것을 볼 수 있습니다. 둘의 증가폭을 맞추어 주기 위해 고안된 수치가 오즈에 로그를 취해준 로짓(Logit) 입니다. 로짓을 수식으로 나타내어 보겠습니다.
\[\text{Logit} = \log \bigg(\frac{x}{1-x}\bigg)\]
로짓 함수의 그래프는 다음과 같이 생겼습니다.
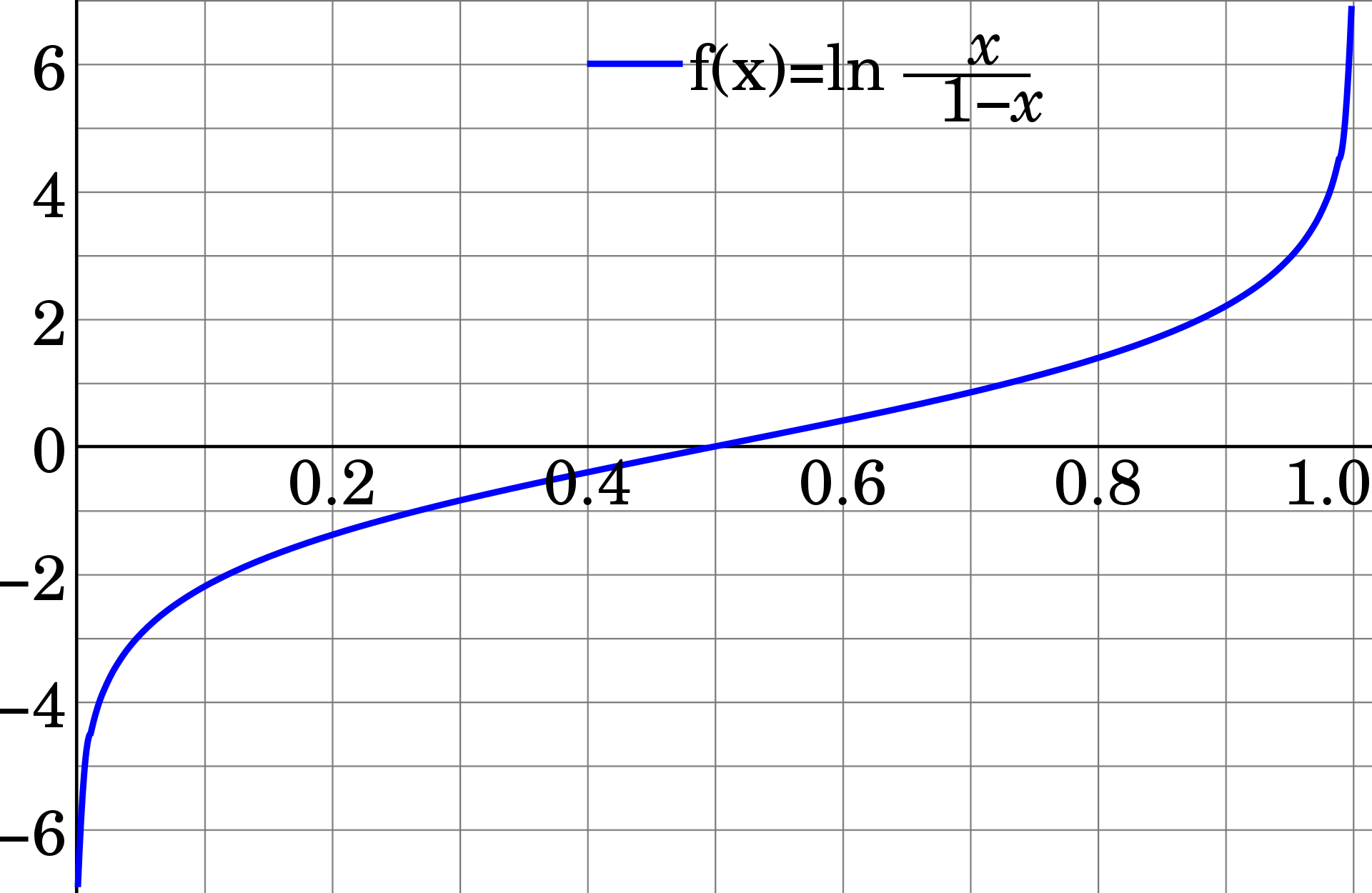
이미지 출처 : 위키피디아 - 로짓
그럼 $p$ 가 변함에 따라 로짓은 어떻게 변하게 될까요? 위에서 사용했던 수치를 사용하여 로짓을 나타내 보겠습니다.
\[\begin{aligned}
\text{Logit}(x = 0.5) &= \log \bigg(\frac{0.5}{1-0.5}\bigg) = \log(1) = 0 \\
\text{Logit}(x = 0.99) &= \log \bigg(\frac{0.99}{1-0.99}\bigg) = \log(99) = 4.595... \\
\text{Logit}(x = 0.01) &= \log \bigg(\frac{0.01}{1-0.01}\bigg) = \log(\frac{1}{99}) = -4.595...
\end{aligned}\]
이제는 $x=0.5$ 일 때의 값이 $0$ 이 되었습니다. 그리고 $x$ 가 $0.5$ 보다 큰 방향으로 변하든지 작은 방향으로 변하든지 로짓값이 동일한 폭으로 증감하는 것을 볼 수 있습니다. 그렇기 때문에 실제로는 오즈보다는 로짓을 더욱 많이 사용하며 로지스틱 함수를 유도하는 데에도 로짓을 사용할 것입니다. 로짓을 $x$ 로 놓고 역함수를 취하면 다음과 같은 함수가 나오게 됩니다.
\[f(x) = \log \bigg(\frac{x}{1-x}\bigg) \xrightarrow{\text{inverse}} \log \bigg(\frac{e^x}{1+e^x}\bigg)\]
도출된 역함수의 식 로그 이하의 부분에서 위와 아래를 $e^{f(x)}$ 로 나누어주면 처음에 보았던 로지스틱 함수와 유사한 형태가도출됩니다.
\[\text{Logistic Function} : \log \bigg(\frac{1}{1+e^{-x}}\bigg)\]
이렇게 도출된 로지스틱 함수는 특성값이 $x$ 인 인스턴스가 특정 클래스에 속할 확률을 구하는 데 사용됩니다. 로지스틱 함수는 로짓 함수의 역함수이므로 다음과 같은 그래프를 나타냅니다.

이미지 출처 : 위키피디아 - 로지스틱 회귀
Logistic Regression
로지스틱 함수가 유도되는 과정을 우리가 모델링하고자 하는 우도(Likelihood) $p$ 를 사용하여 다음과 같이 쓸 수 있습니다.
\[f(x) = \log \big(\frac{x}{1-x}\big) \xrightarrow{\text{inverse}} x = \log \big(\frac{p}{1-p}\big) \xrightarrow{\text{fitting}} ax+b = \log \big(\frac{p}{1-p}\big)\]
선형 회귀(Linear regression)에서 $\hat{f} = X\theta$ 로 나타내었던 것을 이용하여 위 식을 다음과 같이 변형할 수 있습니다.
\[\begin{aligned}
X\theta &= \log \big(\frac{p}{1-p}\big) \\
\because \hat{f} &= X\theta = ax + b \quad \text{(at Linear reg.)} \\
\therefore p &= \log \bigg(\frac{1}{1+e^{-X\theta}}\bigg)
\end{aligned}\]
다음으로 베르누이 시행의 식을 살펴봅시다. 베르누이 시행에서 $y = 1$ 일 때의 확률을 $\mu(x)$ 라고 하면 $P(y \vert x)$ 는 다음과 같이 쓸 수 있습니다.
\[P(y|x) = \mu(x)^y (1-\mu(x))^{1-y}\]
로지스틱 함수를 사용하여 $\mu(x)$ 를 모델링하면 다음과 같은 식이 나오게 됩니다. 아래 식은 하나의 인스턴스에 대한 것이므로 $-X\theta$ 대신 $-\theta^Tx$ 를 사용하였습니다.
\[\mu(x) = P(y = 1|x) = \frac{1}{1+\exp(-\theta^Tx)}\]
이를 전체 인스턴스에 관한 식으로 나타내면 다음과 같이 쓸 수 있습니다.
\[P(Y|X) = \frac{1}{1+e^{-X\theta}}\]
Parameter Estimation
로지스틱 함수가 유도되는 과정을 살펴보았으니 로지스틱 회귀가 파라미터를 추정하는 과정에 대해 살펴보겠습니다. 로지스틱 회귀가 파라미터를 추정하는 방식은 $P(Y \vert X)$ 를 추정하는 최대 조건부 우도 추정에 기반을 두고 있습니다. 최대 조건부 우도 추정식은 최대 우도 추정 식을 변형하여 다음과 같이 쓸 수 있습니다.
\[\hat{\theta} = \text{argmax}_\theta \prod^m_{i = 1} P(Y_i|X_i;\theta) = \text{argmax}_\theta \sum^m_{i = 1} \log \big(P(Y_i|X_i;\theta) \big)\]
베르누이 시행이므로 $P(Y_i
X_i;\theta) = \mu(X_i)^{Y_i}(1 - \mu(X_i))^{1-Y_i}$ 를 대입하여 $\text{argmax}$ 이하의 식을 아래와 같이 변형해 줄 수 있습니다.
\[\begin{aligned}
\log P(Y_i|X_i;\theta) &= Y_i \log \mu(X_i) + (1-Y_i) \log (1-\mu(X_i))\\
&= Y_i\{\log \mu(X_i) - \log (1-\mu(X_i))\} + \log (1-\mu(X_i)) \\
&= Y_i \log \bigg( \frac{\mu(X_i)}{1-\mu(X_i)}\bigg) + \log(1-\mu(X_i)) \\
&= Y_i X_i \theta + \log (1-\mu(X_i)) = Y_i X_i \theta - \log (1+e^{X_i\theta}) \\
\because \log(1-\mu(X_i)) &= \log(1 - \frac{1}{1+e^{-X_i \theta}}) = \log (\frac{1}{1+e^{X_i \theta}})
\end{aligned}\]
변형한 식을 대입합니다.
\[\begin{aligned}
\hat{\theta} &= \text{argmax}_\theta \sum^m_{i = 1} \log \big(P(Y_i|X_i;\theta) \big) \\
&= \text{argmax}_\theta \sum^m_{i = 1} \big\{Y_i X_i \theta - \log (1+e^{X_i\theta})\big\}
\end{aligned}\]
최대 우도 추정에서 했던 것과 같이 $\text{argmax}$ 이하의 식을 $\theta$ 로 미분하여 0이 되는 $\theta$ 를 찾아야 합니다.
\[\begin{aligned}
\frac{\partial}{\partial \theta} \bigg\{\sum^m_{i = 1} Y_i X_i \theta - \log (1+e^{X_i\theta})\bigg\}
&= \bigg\{ \sum^m_{i = 1}Y_iX_i \bigg\} + \bigg\{ \sum^m_{i = 1} -\frac{1}{1+e^{X_i\theta}} \times e^{X_i\theta} \times X_i\bigg\} \\
&= \sum^m_{i = 1} X_i \bigg( Y_i - \frac{e^{X_i \theta}}{1+e^{X_i \theta}}\bigg) \\
&= \sum^m_{i = 1} X_i \big( Y_i - P(Y_i = 1|X_i;\theta)\big) = 0
\end{aligned}\]
이 식은 선형 회귀에서의 최소제곱법 처럼 하나의 닫힌 해가 나오지 않습니다. 그러므로 우리는 경사법을 통해 해를 근사해 나갈 수 밖에 없습니다. 여기서는 최대 조건부 우도를 구하는, 즉 $\text{argmax}$ 인 지점을 구하는 것이므로 경사 상승법을 사용합니다.
with Gradient Ascent
경사 상승법을 통해 해를 추정해봅시다. 경사 하강법에서는 $x_t$ 가 $x_{t+1}$ 로 갱신될 때마다 기울기가 내려가는, 즉 Negative한 방향으로 갱신되므로 다음과 같이 식을 써줄 수 있었습니다.
\[x_{t+1} \leftarrow x_t - h\frac{f^\prime(x_t)}{|f^\prime(x_t)|}\]
경사 상승법은 반대로 기울기가 상승하는 방향으로 갱신해나가므로 부호를 반대로 바꿔주어야 합니다.
\[x_{t+1} \leftarrow x_t + h\frac{f^\prime(x_t)}{|f^\prime(x_t)|}\]
이제 $\theta$ 에 대하여 어떻게 갱신되는지를 알아봅시다. 위에서 미분한 식을 그대로 가져올 수 있습니다.
\[\begin{aligned}
\theta^{t+1}_j \leftarrow \theta^t_j + h\frac{\partial f(\theta^t)}{\partial \theta} &= \theta^t_j + h \bigg\{\sum^m_{i = 1} X_{i,j} \big( Y_i - P(Y_i = 1|X_i;\theta^t\big)\bigg\} \\
&= \theta^t_j + \frac{h}{C} \bigg\{\sum^m_{i = 1} X_{i,j} \bigg( Y_i - \frac{e^{X_i \theta^t}}{1+e^{X_i \theta^t}}\bigg)\bigg\}
\end{aligned}\]
비용 함수로 생각하기
위에서 등장한 것을 활용하여 비용 함수를 최소화하는 과정으로도 생각해 볼 수 있습니다. (위와 같은 과정이지만 비용 함수를 사용하여 설명하는 책들이 많을 것입니다.) 여기서 비용 함수는 음의 로그 우도(Negative log-likelihood) 함수를 사용합니다. 음의 로그 우도 함수는 추정한 우도에 음의 로그를 취해준 $- \log P(Y \vert X)$ 로 표현됩니다. 비용 함수의 식을 다음과 같이 쓸 수 있습니다.
\[\begin{aligned}
-\log P(Y \vert X;\theta) &= -\log \sum^m_{i = 1} \big\{ Y_i \log \mu(X_i) + (1-Y_i) \log (1-\mu(X_i)) \big\} \\
\because P(Y_i|X_i;\theta) &= \mu(X_i)^{Y_i}(1 - \mu(X_i))^{1-Y_i}
\end{aligned}\]
우리의 목적은 비용 함수를 최소화하는 것이므로 $\text{argmin}_\theta$ 을 사용하여 나타낼 수 있습니다.
\[\begin{aligned}
&\text{argmin}_\theta \big(-\log P(Y \vert X;\theta)\big)\\ = &\text{argmin}_\theta
\bigg(-\log \sum_{1 \leq i \leq N} \big\{ Y_i \log \mu(X_i) + (1-Y_i) \log (1-\mu(X_i)) \big\}\bigg)
\end{aligned}\]
위에서 $\text{argmin}$ 이하의 식을 미분하여 나온 식의 값이 0이 되는 $\theta$ 를 경사 하강법으로 찾는 과정은 경사 상승법으로 최대 조건부 우도를 추정한 것과 동일하게 됩니다.
Softmax Regression
개념을 확장시켜 인스턴스를 다중 클래스로 분류하는 작업에 로지스틱 회귀를 적용시켜 봅시다. 로지스틱 회귀의 방법을 다중 분류에 적용한 것을 다항 로지스틱 회귀(Multinomial logistic regression) 또는 소프트맥스 회귀(Softmax regression) 라고 합니다. 샘플 $x$ 에 대해 일련의 파라미터를 곱하여 각 클래스에 속할 점수(Score)를 구합니다. 다음과 같이 클래스 $k$ 에 대한 점수 $s_k(x)$ 를 구할 수 있습니다.
\[s_k(x) = \theta^T_k x\]
모든 클래스에 대해 구해진 점수에 소프트맥스 함수 $\sigma(x)$ 를 취해주어 $k$ 클래스에 속할 확률 $P(Y=k \vert X)$ 를 구할 수 있습니다.
\[P(Y=k|X) = \sigma(s_k(x)) = \frac{\exp(s_k(x))}{\sum^K_{i=1}\exp(s_j(x))}\]
소프트맥스 회귀 모델은 로그 범주 사이의 크로스 엔트로피(Categorical Cross entropy) 를 비용 함수로 사용합니다. 식 자체는 로지스틱 회귀의 비용 함수였던 음의 로그 우도와 동일합니다.
\[\begin{aligned}
-\log P(Y|X;\theta) &= -\log \prod^m_{i=1}\prod^K_{k=1}\pi_k^{y_k} \\
&= - \sum^m_{i=1}\sum^K_{k=1} y_k \log \pi_k
\end{aligned}\]
여기서도 비용 함수를 최소화 해야 하므로 $\text{argmin}$ 을 사용하여 나타낼 수 있습니다.
\[\begin{aligned}
&\text{argmin}_\theta \big( -\log P(Y|X;\theta) \big) \\
= &\text{argmin}_\theta \bigg(- \sum^m_{i=1}\sum^K_{k=1} y_k \log \pi_k \bigg)
\end{aligned}\]
$\text{argmin}$ 이하의 식을 미분하여 0이되는 $\theta$ 를 찾는 수식은 다음과 같습니다. 아래 식을 만족하는 $\theta$ 의 값 역시 열린 해의 형태이므로 경사 하강법을 통해 근사해나가야 합니다.
\[\frac{1}{m}\sum^m_{i = 1}\sum^K_{k=1} X_{i,j} \big(P(Y_i = k|X_i;\theta) - Y_i\big) = 0\]
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 강의를 바탕으로 작성하였습니다.
Logistic Regression
나이브 베이즈 분류기 에서는 최적의 분류기란 어떤 것인지에 대해 아래의 그림을 통해 알아보았습니다. 아래는 두 분류기의 확률 밀도 함수를 점선과 실선으로 각각 나타낸 것입니다.

이미지 출처 : 인공지능 및 기계학습 개론 학습자료
위 그림에서 베이즈 위험(Bayes’ risk)을 통해 점선보다 실선 분류기가 더 좋은 성능을 나타낼 것으로 판단하였습니다. 실선 분류기의 베이즈 위험이 더 작았기 때문입니다. 실선 분류기가 점선보다 베이즈 위험이 낮은 이유는 결정 경계(Decision boundary)에서 확률이 더욱 급격하게 변했기 때문입니다. 즉, 결정 경계에서 급하게 변할수록 더 좋은 분류기가 되는 것이지요.
이번 게시물에서 다루게 될 로지스틱 회귀는 결정 경계에서 확률이 급격하게 변하는 분류기 입니다. 로지스틱 회귀에서는 결정 경계에서 확률이 급격히 변하는 시그모이드 함수를 사용합니다. 시그모이드 함수란 무엇인지 알아봅시다.
Sigmoid
시그모이드 함수(Sigmoid function) 란 실수 정의역 범위에서 최댓값이 1이하이고 최솟값이 0이상인 미분가능한 단조증가함수입니다. 시그모이드 함수는 특정한 하나의 함수가 아니라 이런 조건을 만족하는 함수 집합입니다. $\tanh{x} , \arctan{x} , 1/(1+e^{-x})$ 등 다양한 형태의 시그모이드 함수가 있습니다. 이 중 세 번째에 있는 함수를 로지스틱 함수(Logistic function) 라고 합니다. 바로 이 로지스틱 함수를 사용한 회귀이기 때문에 로지스틱 회귀라는 이름이 붙은 것입니다.
로지스틱 함수를 사용하는 이유는 미분 계산이 쉽기 때문입니다. 일반적으로 분류기를 최적화(Optimization)하기 위해서는 특정 확률이 최대 혹은 최소가 되는 점을 찾습니다. 이러한 점을 찾는 데에 미분 계산은 필수적인 관문입니다. 로지스틱 함수는 이 미분 계산을 쉽게 만들어주기 때문에 데이터셋이 많아지더라도 수행 시간을 적절한 선에서 유지할 수 있다는 장점을 가지고 있습니다.
Logistic function
로지스틱 함수의 수식을 다시 써보겠습니다.
\[y = \frac{1}{1+e^{-x}}\]로지스틱 함수의 형태가 위와 같이 된 이유는 무엇일까요? 시작은 오즈(Odds) 라는 개념에서부터 시작합니다. 오즈는 확률의 또 다른 표현법 중 하나입니다. 어떤 사건이 일어날 확률을 $x$ 라고 했을 때 오즈는 다음와 가같이 나타낼 수 있습니다.
\[\text{Odds} = \frac{x}{1-x}\]오즈는 한 가지 단점을 가지고 있습니다. $x$ 가 커지는 경우에 대해서는 값이 양의 무한대로 증가하지만 $x$ 가 작아지는 경우에 대해서는 0이하로는 작아지지 않는다는 것이지요. $x = 0.5$ 일 때를 기준으로 $x = 0.99$ 로 매우 클 때와 $x = 0.01$ 로 매우 작을 때 오즈가 어떻게 변하는지 봅시다.
\[\begin{aligned} \text{Odds}(x = 0.5) &= \frac{0.5}{1-0.5} = 1 \\ \text{Odds}(x = 0.99) &= \frac{0.99}{1-0.99} = 99 \\ \text{Odds}(x = 0.01) &= \frac{0.01}{1-0.01} = \frac{1}{99} \end{aligned}\]$x = 0.5$ 일 때, 즉 어떤 사건이 일어날 때와 일어나지 않을 때의 확률이 동일할 때의 확률은 $1$ 입니다. 이를 기준으로 $x > 0.5$ 인 방향으로 변하면 오즈가 급격하게 커지지만 $x < 0.5$ 인 방향으로 변할 때는 오즈가 완만하게 줄어드는 것을 볼 수 있습니다. 둘의 증가폭을 맞추어 주기 위해 고안된 수치가 오즈에 로그를 취해준 로짓(Logit) 입니다. 로짓을 수식으로 나타내어 보겠습니다.
\[\text{Logit} = \log \bigg(\frac{x}{1-x}\bigg)\]로짓 함수의 그래프는 다음과 같이 생겼습니다.

이미지 출처 : 위키피디아 - 로짓
그럼 $p$ 가 변함에 따라 로짓은 어떻게 변하게 될까요? 위에서 사용했던 수치를 사용하여 로짓을 나타내 보겠습니다.
\[\begin{aligned} \text{Logit}(x = 0.5) &= \log \bigg(\frac{0.5}{1-0.5}\bigg) = \log(1) = 0 \\ \text{Logit}(x = 0.99) &= \log \bigg(\frac{0.99}{1-0.99}\bigg) = \log(99) = 4.595... \\ \text{Logit}(x = 0.01) &= \log \bigg(\frac{0.01}{1-0.01}\bigg) = \log(\frac{1}{99}) = -4.595... \end{aligned}\]이제는 $x=0.5$ 일 때의 값이 $0$ 이 되었습니다. 그리고 $x$ 가 $0.5$ 보다 큰 방향으로 변하든지 작은 방향으로 변하든지 로짓값이 동일한 폭으로 증감하는 것을 볼 수 있습니다. 그렇기 때문에 실제로는 오즈보다는 로짓을 더욱 많이 사용하며 로지스틱 함수를 유도하는 데에도 로짓을 사용할 것입니다. 로짓을 $x$ 로 놓고 역함수를 취하면 다음과 같은 함수가 나오게 됩니다.
\[f(x) = \log \bigg(\frac{x}{1-x}\bigg) \xrightarrow{\text{inverse}} \log \bigg(\frac{e^x}{1+e^x}\bigg)\]도출된 역함수의 식 로그 이하의 부분에서 위와 아래를 $e^{f(x)}$ 로 나누어주면 처음에 보았던 로지스틱 함수와 유사한 형태가도출됩니다.
\[\text{Logistic Function} : \log \bigg(\frac{1}{1+e^{-x}}\bigg)\]이렇게 도출된 로지스틱 함수는 특성값이 $x$ 인 인스턴스가 특정 클래스에 속할 확률을 구하는 데 사용됩니다. 로지스틱 함수는 로짓 함수의 역함수이므로 다음과 같은 그래프를 나타냅니다.

이미지 출처 : 위키피디아 - 로지스틱 회귀
Logistic Regression
로지스틱 함수가 유도되는 과정을 우리가 모델링하고자 하는 우도(Likelihood) $p$ 를 사용하여 다음과 같이 쓸 수 있습니다.
\[f(x) = \log \big(\frac{x}{1-x}\big) \xrightarrow{\text{inverse}} x = \log \big(\frac{p}{1-p}\big) \xrightarrow{\text{fitting}} ax+b = \log \big(\frac{p}{1-p}\big)\]선형 회귀(Linear regression)에서 $\hat{f} = X\theta$ 로 나타내었던 것을 이용하여 위 식을 다음과 같이 변형할 수 있습니다.
\[\begin{aligned} X\theta &= \log \big(\frac{p}{1-p}\big) \\ \because \hat{f} &= X\theta = ax + b \quad \text{(at Linear reg.)} \\ \therefore p &= \log \bigg(\frac{1}{1+e^{-X\theta}}\bigg) \end{aligned}\]다음으로 베르누이 시행의 식을 살펴봅시다. 베르누이 시행에서 $y = 1$ 일 때의 확률을 $\mu(x)$ 라고 하면 $P(y \vert x)$ 는 다음과 같이 쓸 수 있습니다.
\[P(y|x) = \mu(x)^y (1-\mu(x))^{1-y}\]로지스틱 함수를 사용하여 $\mu(x)$ 를 모델링하면 다음과 같은 식이 나오게 됩니다. 아래 식은 하나의 인스턴스에 대한 것이므로 $-X\theta$ 대신 $-\theta^Tx$ 를 사용하였습니다.
\[\mu(x) = P(y = 1|x) = \frac{1}{1+\exp(-\theta^Tx)}\]이를 전체 인스턴스에 관한 식으로 나타내면 다음과 같이 쓸 수 있습니다.
\[P(Y|X) = \frac{1}{1+e^{-X\theta}}\]Parameter Estimation
로지스틱 함수가 유도되는 과정을 살펴보았으니 로지스틱 회귀가 파라미터를 추정하는 과정에 대해 살펴보겠습니다. 로지스틱 회귀가 파라미터를 추정하는 방식은 $P(Y \vert X)$ 를 추정하는 최대 조건부 우도 추정에 기반을 두고 있습니다. 최대 조건부 우도 추정식은 최대 우도 추정 식을 변형하여 다음과 같이 쓸 수 있습니다.
\[\hat{\theta} = \text{argmax}_\theta \prod^m_{i = 1} P(Y_i|X_i;\theta) = \text{argmax}_\theta \sum^m_{i = 1} \log \big(P(Y_i|X_i;\theta) \big)\]| 베르누이 시행이므로 $P(Y_i | X_i;\theta) = \mu(X_i)^{Y_i}(1 - \mu(X_i))^{1-Y_i}$ 를 대입하여 $\text{argmax}$ 이하의 식을 아래와 같이 변형해 줄 수 있습니다. |
변형한 식을 대입합니다.
\[\begin{aligned} \hat{\theta} &= \text{argmax}_\theta \sum^m_{i = 1} \log \big(P(Y_i|X_i;\theta) \big) \\ &= \text{argmax}_\theta \sum^m_{i = 1} \big\{Y_i X_i \theta - \log (1+e^{X_i\theta})\big\} \end{aligned}\]최대 우도 추정에서 했던 것과 같이 $\text{argmax}$ 이하의 식을 $\theta$ 로 미분하여 0이 되는 $\theta$ 를 찾아야 합니다.
\[\begin{aligned} \frac{\partial}{\partial \theta} \bigg\{\sum^m_{i = 1} Y_i X_i \theta - \log (1+e^{X_i\theta})\bigg\} &= \bigg\{ \sum^m_{i = 1}Y_iX_i \bigg\} + \bigg\{ \sum^m_{i = 1} -\frac{1}{1+e^{X_i\theta}} \times e^{X_i\theta} \times X_i\bigg\} \\ &= \sum^m_{i = 1} X_i \bigg( Y_i - \frac{e^{X_i \theta}}{1+e^{X_i \theta}}\bigg) \\ &= \sum^m_{i = 1} X_i \big( Y_i - P(Y_i = 1|X_i;\theta)\big) = 0 \end{aligned}\]이 식은 선형 회귀에서의 최소제곱법 처럼 하나의 닫힌 해가 나오지 않습니다. 그러므로 우리는 경사법을 통해 해를 근사해 나갈 수 밖에 없습니다. 여기서는 최대 조건부 우도를 구하는, 즉 $\text{argmax}$ 인 지점을 구하는 것이므로 경사 상승법을 사용합니다.
with Gradient Ascent
경사 상승법을 통해 해를 추정해봅시다. 경사 하강법에서는 $x_t$ 가 $x_{t+1}$ 로 갱신될 때마다 기울기가 내려가는, 즉 Negative한 방향으로 갱신되므로 다음과 같이 식을 써줄 수 있었습니다.
\[x_{t+1} \leftarrow x_t - h\frac{f^\prime(x_t)}{|f^\prime(x_t)|}\]경사 상승법은 반대로 기울기가 상승하는 방향으로 갱신해나가므로 부호를 반대로 바꿔주어야 합니다.
\[x_{t+1} \leftarrow x_t + h\frac{f^\prime(x_t)}{|f^\prime(x_t)|}\]이제 $\theta$ 에 대하여 어떻게 갱신되는지를 알아봅시다. 위에서 미분한 식을 그대로 가져올 수 있습니다.
\[\begin{aligned} \theta^{t+1}_j \leftarrow \theta^t_j + h\frac{\partial f(\theta^t)}{\partial \theta} &= \theta^t_j + h \bigg\{\sum^m_{i = 1} X_{i,j} \big( Y_i - P(Y_i = 1|X_i;\theta^t\big)\bigg\} \\ &= \theta^t_j + \frac{h}{C} \bigg\{\sum^m_{i = 1} X_{i,j} \bigg( Y_i - \frac{e^{X_i \theta^t}}{1+e^{X_i \theta^t}}\bigg)\bigg\} \end{aligned}\]비용 함수로 생각하기
위에서 등장한 것을 활용하여 비용 함수를 최소화하는 과정으로도 생각해 볼 수 있습니다. (위와 같은 과정이지만 비용 함수를 사용하여 설명하는 책들이 많을 것입니다.) 여기서 비용 함수는 음의 로그 우도(Negative log-likelihood) 함수를 사용합니다. 음의 로그 우도 함수는 추정한 우도에 음의 로그를 취해준 $- \log P(Y \vert X)$ 로 표현됩니다. 비용 함수의 식을 다음과 같이 쓸 수 있습니다.
\[\begin{aligned} -\log P(Y \vert X;\theta) &= -\log \sum^m_{i = 1} \big\{ Y_i \log \mu(X_i) + (1-Y_i) \log (1-\mu(X_i)) \big\} \\ \because P(Y_i|X_i;\theta) &= \mu(X_i)^{Y_i}(1 - \mu(X_i))^{1-Y_i} \end{aligned}\]우리의 목적은 비용 함수를 최소화하는 것이므로 $\text{argmin}_\theta$ 을 사용하여 나타낼 수 있습니다.
\[\begin{aligned} &\text{argmin}_\theta \big(-\log P(Y \vert X;\theta)\big)\\ = &\text{argmin}_\theta \bigg(-\log \sum_{1 \leq i \leq N} \big\{ Y_i \log \mu(X_i) + (1-Y_i) \log (1-\mu(X_i)) \big\}\bigg) \end{aligned}\]위에서 $\text{argmin}$ 이하의 식을 미분하여 나온 식의 값이 0이 되는 $\theta$ 를 경사 하강법으로 찾는 과정은 경사 상승법으로 최대 조건부 우도를 추정한 것과 동일하게 됩니다.
Softmax Regression
개념을 확장시켜 인스턴스를 다중 클래스로 분류하는 작업에 로지스틱 회귀를 적용시켜 봅시다. 로지스틱 회귀의 방법을 다중 분류에 적용한 것을 다항 로지스틱 회귀(Multinomial logistic regression) 또는 소프트맥스 회귀(Softmax regression) 라고 합니다. 샘플 $x$ 에 대해 일련의 파라미터를 곱하여 각 클래스에 속할 점수(Score)를 구합니다. 다음과 같이 클래스 $k$ 에 대한 점수 $s_k(x)$ 를 구할 수 있습니다.
\[s_k(x) = \theta^T_k x\]모든 클래스에 대해 구해진 점수에 소프트맥스 함수 $\sigma(x)$ 를 취해주어 $k$ 클래스에 속할 확률 $P(Y=k \vert X)$ 를 구할 수 있습니다.
\[P(Y=k|X) = \sigma(s_k(x)) = \frac{\exp(s_k(x))}{\sum^K_{i=1}\exp(s_j(x))}\]소프트맥스 회귀 모델은 로그 범주 사이의 크로스 엔트로피(Categorical Cross entropy) 를 비용 함수로 사용합니다. 식 자체는 로지스틱 회귀의 비용 함수였던 음의 로그 우도와 동일합니다.
\[\begin{aligned} -\log P(Y|X;\theta) &= -\log \prod^m_{i=1}\prod^K_{k=1}\pi_k^{y_k} \\ &= - \sum^m_{i=1}\sum^K_{k=1} y_k \log \pi_k \end{aligned}\]여기서도 비용 함수를 최소화 해야 하므로 $\text{argmin}$ 을 사용하여 나타낼 수 있습니다.
\[\begin{aligned} &\text{argmin}_\theta \big( -\log P(Y|X;\theta) \big) \\ = &\text{argmin}_\theta \bigg(- \sum^m_{i=1}\sum^K_{k=1} y_k \log \pi_k \bigg) \end{aligned}\]$\text{argmin}$ 이하의 식을 미분하여 0이되는 $\theta$ 를 찾는 수식은 다음과 같습니다. 아래 식을 만족하는 $\theta$ 의 값 역시 열린 해의 형태이므로 경사 하강법을 통해 근사해나가야 합니다.
\[\frac{1}{m}\sum^m_{i = 1}\sum^K_{k=1} X_{i,j} \big(P(Y_i = k|X_i;\theta) - Y_i\big) = 0\]
Comments