나이브 베이즈 분류기 (Naive Bayes Classifier)
08 Apr 2020 | Machine-Learning
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 강의를 바탕으로 작성하였습니다.
Bayes Decision Theory
나이브 베이즈 분류기(Naive Bayes Classifier) 는 간단하고 여러 분류 문제에 적용하기 쉬우면서도 뛰어난 성능을 보이는 분류기 중 하나입니다. 인스턴스의 레이블을 예측할 때 베이즈 결정 이론(Bayes decision theory) 을 사용하여 판단하기 때문에 이러한 이름이 붙었습니다. 이번 게시물에서는 베이즈 결정 이론이란 무엇인지? 그리고 베이즈 분류기는 이름 앞에 왜 나이브(Naive)라는 수식어가 붙는 지를 알아봅시다.
최적(Optimal)의 분류기란?
다음의 그림을 통해 최적의 분류기란 어떤 것인지 알아보도록 합시다. 아래 그림에는 점선으로 나타나는 분류기 하나와 실선으로 나타나는 분류기 하나가 있습니다.

이미지 출처 : 인공지능 및 기계학습 개론 학습자료
위 그림에서 $x$ 축은 특성값을 나타내며 각 $x$ 에서의 $y$ 값은 특정 클래스를 나타낼 확률을 나타냅니다. 중간에 두 그래프가 만나는 부분을 결정 경계(Decision boundary) 라고 하며 이 결정 경계를 기준으로 $x$ 가 왼쪽인지 오른쪽인지에 따라 분류기가 예측하는 값인 $\hat{y}$ 가 달라지게 됩니다. 그렇다면 두 분류기 중 어떤 것이 더 좋은 분류기일까요? 분류기의 성능은 위 그림에도 나와있는 베이즈 위험(Bayes Risk) 에 따라 판단할 수 있습니다. 베이즈 위험이 무엇인지 알아보기 위해 위 그림에 임의의 $x_1$ 에 해당하는 세로선을 그어 보겠습니다.

이미지 출처 : 인공지능 및 기계학습 개론 학습자료
위 그림에서 $x_1$ 은 결정 경계 왼쪽에 위치하고 있으므로 $x_1$ 을 입력한다면 두 분류기 모두 초록 클래스로 분류할 것입니다. 하지만 이 점에서도 각각의 분류기는 빨강 클래스일 확률을 가지고 있습니다. 점선 분류기는 주황색 점으로 나타나는 위치의 $y$ 값인 $y_1$ , 실선 분류기는 파란색 점으로 나타나는 위치의 $y$ 값인 $y_2$ 만큼이 특성값 $x_1$ 에 대하여 빨강 클래스일 확률입니다. 하지만 분류기는 이런 확률을 무시하고 초록 클래스를 선택합니다. 이렇게 무시되는 확률을 모든 $x$ 에 대해 적분한 것이 베이즈 위험입니다. 따라서 점선 분류기의 베이즈 위험은 위 그림에서 (하늘색 + 갈색)으로 나타나는 부분인 $S_1 + S_2 + S_3$ 가 됩니다. 그리고 실선 분류기의 베이즈 위험은 위 그림에서 갈색으로 나타나는 부분인 $S_3$ 이 됩니다. 더 좋은 분류기라면 클래스를 선택할 때 해당 클래스가 아닐 확률, 즉 베이즈 위험을 더 작게 할 것입니다. 따라서 위 그림에서는 베이즈 위험이 더 적은 실선 분류기가 더 좋은 성능을 보인다고 할 수 있습니다.
최적의 분류기라면 베이즈 위험을 최소화해야 할 것입니다. 클래스를 잘못 선택할 확률을 가장 적게 하는 것이므로 최적의 분류기 $f^*$ 를 다음과 같은 수식으로 나타낼 수 있습니다.
\[f^* = \text{argmin}_f P(f(X) \neq Y)\]
위 식을 전체 클래스가 2개 뿐인 이진 분류(Binary classification)에 대해서는 다음과 같이 쓸 수도 있습니다.
\[f^* = \text{argmax}_{Y=y} P(Y=y\vert X=x)\]
Bayes Classifier
이제는 최적의 분류기 $f^*$ 에 대한 식을 우리가 다룰 수 있는 형태로 식을 변형할 차례입니다. 최대 사후확률 추정 에서 주어진 데이터셋으로부터 특정 클래스일 확률을 추정하는 방법을 배웠습니다. 최대 사후확률 추정에서 사용했던 베이즈 정리를 사용하여 위 식을 다음과 같이 바꿔쓸 수 있습니다.
\[f^* = \text{argmax}_{Y=y} P(Y=y\vert X=x) = \text{argmax}_{Y=y} P(X=x\vert Y=y)P(Y=y) \\
\text{ } \\
\because P(Y=y \vert X=x) = \frac{P(X=x \vert Y=y)P(Y=y)}{P(X=x)} \quad \text{and} \quad P(X) \text{ is constant} \\\]
변형한 베이즈 분류기 $f^*$ 의 수식을 다시 써보겠습니다.
\[f^* = \text{argmax}_{Y=y} P(X=x\vert Y=y)P(Y=y)\]
위 식에서 $\text{argmax}$ 이하의 두 항 중에서 왼쪽을 Class conditional density라 하고 Class prior라고 합니다.
Naive Bayes Classifier
이제 왜 나이브 베이즈 분류기의 앞에 나이브(Naive)라는 수식어가 붙는지 알아볼 것입니다. 분류기를 만들 때 가장 문제가 되는 것은 데이터셋 내에 있는 특성끼리 어떤 관계를 맺고 있는지 알 수 없기 때문입니다. 데이터셋 내에 있는 모든 특성이 관계를 맺고 있다면 클래스가 $k$ 개이고 특성이 $d$ 개일 때 Class conditional density를 구하기 위해서는 $(2^d-1)k$ 개의 파라미터가 필요합니다. 그리고 Class prior를 구하기 위해서는 $k-1$ 개의 파라미터가 필요하지요. 규칙 기반 학습 에서 사용했던 예시 데이터셋에서 모든 특성이 관계를 맺고 있다면 몇 개의 파라미터가 필요할까요?
하늘 상태
온도
습도
바람
해수 온도
일기 예보
물놀이를 나갈까?
맑음
따듯함
보통
강함
따듯함
일정함
예
맑음
따듯함
높음
강함
따듯함
일정함
예
흐림
추움
높음
강함
따듯함
가변적
아니오
맑음
따듯함
높음
강함
차가움
가변적
예
클래스의 개수 $k = 1$ 이고, 특성의 개수 $d = 6$ 이므로 $2 \cdot (2^6-1) \times (2 - 1) = 126$ 개의 파라미터가 필요하게 됩니다. 모든 특성이 관계를 맺고 있다면 상당히 간단해보이는 데이터셋으로부터 분류 기준을 이끌어 내는 데만도 많은 파라미터를 필요로 하게 됩니다. 실제 데이터는 수십 ~ 수백 개의 특성을 가지고 있는 경우가 많습니다. 특성의 개수에 따라 필요한 파라미터의 개수는 기하급수적으로 늘어나므로 특성 사이의 관계를 어떻게 해결해주지 않으면 필요한 파라미터의 개수는 엄청나게 늘어날 것입니다. 실제로 20개의 특성을 가진 데이터셋이라면 필요한 파라미터의 개수는 100만개가 넘습니다. 이 문제를 해결해줄 조건부 독립에 대해 알아봅시다.
Conditional Independence
조건부 독립(Conditional Independence) 은 특성의 개수를 줄이지 않고도 필요한 파라미터의 개수를 줄일 수 있는 방법입니다. 조건부 독립이 무엇이길래 이런 일을 할 수 있는 것일까요? 조건부 독립은 임의의 관계에 있는 두 사건이 주어진 조건하에서는 독립이 되는 경우를 말합니다. 조건부 독립의 예시를 몇 가지 들어봅시다.
“비가 오는 사건” 과 “천둥이 치는 사건” 이 있다고 해봅시다. 두 사건 사이에는 어떤 관계가 있어 보입니다. 그런데 가운데 “번개가 쳤다” 라는 조건이 주어졌다고 해봅시다. “번개가 쳤다” 라는 조건하에서는 “천둥이 치는 사건” 과 “비가 오는 사건” 은 독립이 되어버립니다. 각각을 확률로 나타내어 보겠습니다. (해당 예시에서 마른 하늘에 번개가 치는 것은 예외로 합니다.)
\[\begin{aligned}
P(천둥=침|비=옴) &\neq P(천둥=침)\\
P(천둥=침|비=옴, 번개=침) &= P(천둥=침|번개=침)\\
P(비|천둥=침, 번개=침) &= P(비=옴|번개=침)\\
\because P(천둥=침, 비|번개=침) &= P(천둥=침|번개=침)P(비=옴|번개=침)
\end{aligned}\]
천둥과 비는 독립이 아니므로 비가 왔을 때 천둥이 칠 확률 $P(천둥 \vert 비)$ 와 아무런 조건이 없을 때 천둥이 칠 확률 $P(천둥)$ 은 같지 않습니다. 비가 올 때 천둥이 칠 확률이 훨씬 높겠지요. 하지만 번개라는 조건이 주어지면 다른 두 사건은 이 조건에
두 번째 예시는 그림과 함께 알아봅시다. 아래 그림은 지휘관과 지휘관의 명령을 따르는 직원 A,B 를 그림으로 나타낸 것입니다.
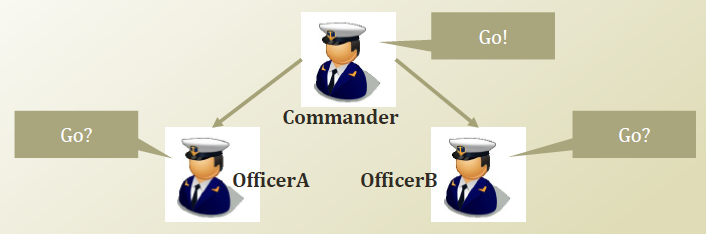
이미지 출처 : 인공지능 및 기계학습 개론 학습자료
먼저 A가 지휘관의 명령을 듣지 못하는 상태, 즉 지휘관의 명령을 알 수 없는 상태라고 가정해 봅시다. 이 경우에는 B가 앞으로 가는 것을 보았을 때와 그렇지 않을 때 A가 앞으로 갈 확률은 다를 것입니다. 아무래도 B가 앞으로 가는 것을 본다면 ‘지휘관이 B에게 명령을 내렸겠구나’라고 생각하고 앞으로 가게 되겠지요. 수식으로는 아래와 같이 나타낼 수 있습니다.
\[P(\text{OfficerA=Go} \vert \text{OfficerB=Go}) \neq P(\text{OfficerA=Go})\]
이번에는 A가 지휘관의 명령을 들을 수 있는 상태라고 가정하고 같은 상황에 대한 확률을 구해봅시다. 지휘관의 명령을 들을 수 있다면 B가 앞으로 가든 말든 A가 앞으로 갈 확률에는 차이가 없습니다. B가 앞으로 가든지 말든지 지휘관의 명령만 따라서 움직이면 되기 때문입니다.
\[P(\text{OfficerA=Go} \vert \text{OfficerB=Go, Commander = Go}) = P(\text{OfficerA=Go} \vert \text{Commander=Go})\]
이렇게 독립이 아닌 두 사건에 대해 특정 조건이 개입했을 때 조건부 확률이 독립이 되는 관계를 조건부 독립이라고 합니다. 조건 $y$ 에 대하여 조건부 독립인 사건 $x_1, \cdots, x_n$ 은 다음과 같은 수식을 만족합니다.
\[( \forall x_1, x_2,y) \\
\begin{aligned}
P(x_1 \vert x_2, y) &= P(x_1 \vert y) \\
\therefore P(x_1,x_2 \vert y) &= P(x_1 \vert y)P(x_2 \vert y)
\end{aligned}\]
마지막 등식을 사용하여 Class conditional density의 항을 다음과 같이 변형할 수 있습니다.
\[P(X= \{x_1, ..., x_d\} \vert Y=y) \rightarrow \prod^d_{i=1} P(X_i = x_i \vert Y=y)\]
Naive Bayes Classifier
베이즈 분류기를 수식으로 나타낸 $f^*$ 에 변형된 수식을 적용해봅시다.
\[\begin{aligned}
f^* &= \text{argmax}_{Y=y} P(X = x \vert Y = y) P(Y = y) \\
&\approx \text{argmax}_{Y=y} P(Y = y) \prod_{1 \leq i \leq d} P(X_i = x_i \vert Y=y)
\end{aligned}\]
특성 $x_1, … ,x_d$ 가 모두 관계를 맺고 있을 때 Class conditional density 항을 구하기 위해서 필요한 파라미터의 개수는 $(2^d-1)k$ 였습니다. 식을 변형한 후에는 어떻게 될까요? 변형한 식에서 Class conditional density 부분을 구하기 위해 필요한 파라미터의 개수는 $d \cdot k$ 개가 됩니다. 위에서 했던 것처럼 특성이 $6$ 개, 클래스가 $2$ 개인 분류 문제를 위해서 필요한 파라미터의 개수를 구해봅시다. Class prior 항을 구하기 위해 필요한 파라미터의 개수는 $k-1$ 로 동일하므로 $6 \cdot 2 \times 1 = 12$ 개가 됩니다. 훨씬 더 줄어든 것을 볼 수 있습니다.
하지만 현실세계에서는 특성들이 서로 조건부독립을 만족하지 않는 경우가 대부분입니다. 파라미터의 개수를 줄이기 위한 가정이 말 그대로 너무 순진한(Naive, 나이브) 한 가정이기 때문에 이 가정을 사용한 베이즈 분류기를 나이브 베이즈 분류기(Naive Bayes Classifier) 라고 부릅니다. 나이브 베이즈 분류기는 비록 특수한 가정을 사용하였지만 몇몇 태스크에서 다른 복잡한 모델보다도 더 좋은 성능을 내기도 합니다.
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 강의를 바탕으로 작성하였습니다.
Bayes Decision Theory
나이브 베이즈 분류기(Naive Bayes Classifier) 는 간단하고 여러 분류 문제에 적용하기 쉬우면서도 뛰어난 성능을 보이는 분류기 중 하나입니다. 인스턴스의 레이블을 예측할 때 베이즈 결정 이론(Bayes decision theory) 을 사용하여 판단하기 때문에 이러한 이름이 붙었습니다. 이번 게시물에서는 베이즈 결정 이론이란 무엇인지? 그리고 베이즈 분류기는 이름 앞에 왜 나이브(Naive)라는 수식어가 붙는 지를 알아봅시다.
최적(Optimal)의 분류기란?
다음의 그림을 통해 최적의 분류기란 어떤 것인지 알아보도록 합시다. 아래 그림에는 점선으로 나타나는 분류기 하나와 실선으로 나타나는 분류기 하나가 있습니다.

이미지 출처 : 인공지능 및 기계학습 개론 학습자료
위 그림에서 $x$ 축은 특성값을 나타내며 각 $x$ 에서의 $y$ 값은 특정 클래스를 나타낼 확률을 나타냅니다. 중간에 두 그래프가 만나는 부분을 결정 경계(Decision boundary) 라고 하며 이 결정 경계를 기준으로 $x$ 가 왼쪽인지 오른쪽인지에 따라 분류기가 예측하는 값인 $\hat{y}$ 가 달라지게 됩니다. 그렇다면 두 분류기 중 어떤 것이 더 좋은 분류기일까요? 분류기의 성능은 위 그림에도 나와있는 베이즈 위험(Bayes Risk) 에 따라 판단할 수 있습니다. 베이즈 위험이 무엇인지 알아보기 위해 위 그림에 임의의 $x_1$ 에 해당하는 세로선을 그어 보겠습니다.

이미지 출처 : 인공지능 및 기계학습 개론 학습자료
위 그림에서 $x_1$ 은 결정 경계 왼쪽에 위치하고 있으므로 $x_1$ 을 입력한다면 두 분류기 모두 초록 클래스로 분류할 것입니다. 하지만 이 점에서도 각각의 분류기는 빨강 클래스일 확률을 가지고 있습니다. 점선 분류기는 주황색 점으로 나타나는 위치의 $y$ 값인 $y_1$ , 실선 분류기는 파란색 점으로 나타나는 위치의 $y$ 값인 $y_2$ 만큼이 특성값 $x_1$ 에 대하여 빨강 클래스일 확률입니다. 하지만 분류기는 이런 확률을 무시하고 초록 클래스를 선택합니다. 이렇게 무시되는 확률을 모든 $x$ 에 대해 적분한 것이 베이즈 위험입니다. 따라서 점선 분류기의 베이즈 위험은 위 그림에서 (하늘색 + 갈색)으로 나타나는 부분인 $S_1 + S_2 + S_3$ 가 됩니다. 그리고 실선 분류기의 베이즈 위험은 위 그림에서 갈색으로 나타나는 부분인 $S_3$ 이 됩니다. 더 좋은 분류기라면 클래스를 선택할 때 해당 클래스가 아닐 확률, 즉 베이즈 위험을 더 작게 할 것입니다. 따라서 위 그림에서는 베이즈 위험이 더 적은 실선 분류기가 더 좋은 성능을 보인다고 할 수 있습니다.
최적의 분류기라면 베이즈 위험을 최소화해야 할 것입니다. 클래스를 잘못 선택할 확률을 가장 적게 하는 것이므로 최적의 분류기 $f^*$ 를 다음과 같은 수식으로 나타낼 수 있습니다.
\[f^* = \text{argmin}_f P(f(X) \neq Y)\]위 식을 전체 클래스가 2개 뿐인 이진 분류(Binary classification)에 대해서는 다음과 같이 쓸 수도 있습니다.
\[f^* = \text{argmax}_{Y=y} P(Y=y\vert X=x)\]Bayes Classifier
이제는 최적의 분류기 $f^*$ 에 대한 식을 우리가 다룰 수 있는 형태로 식을 변형할 차례입니다. 최대 사후확률 추정 에서 주어진 데이터셋으로부터 특정 클래스일 확률을 추정하는 방법을 배웠습니다. 최대 사후확률 추정에서 사용했던 베이즈 정리를 사용하여 위 식을 다음과 같이 바꿔쓸 수 있습니다.
\[f^* = \text{argmax}_{Y=y} P(Y=y\vert X=x) = \text{argmax}_{Y=y} P(X=x\vert Y=y)P(Y=y) \\ \text{ } \\ \because P(Y=y \vert X=x) = \frac{P(X=x \vert Y=y)P(Y=y)}{P(X=x)} \quad \text{and} \quad P(X) \text{ is constant} \\\]변형한 베이즈 분류기 $f^*$ 의 수식을 다시 써보겠습니다.
\[f^* = \text{argmax}_{Y=y} P(X=x\vert Y=y)P(Y=y)\]위 식에서 $\text{argmax}$ 이하의 두 항 중에서 왼쪽을 Class conditional density라 하고 Class prior라고 합니다.
Naive Bayes Classifier
이제 왜 나이브 베이즈 분류기의 앞에 나이브(Naive)라는 수식어가 붙는지 알아볼 것입니다. 분류기를 만들 때 가장 문제가 되는 것은 데이터셋 내에 있는 특성끼리 어떤 관계를 맺고 있는지 알 수 없기 때문입니다. 데이터셋 내에 있는 모든 특성이 관계를 맺고 있다면 클래스가 $k$ 개이고 특성이 $d$ 개일 때 Class conditional density를 구하기 위해서는 $(2^d-1)k$ 개의 파라미터가 필요합니다. 그리고 Class prior를 구하기 위해서는 $k-1$ 개의 파라미터가 필요하지요. 규칙 기반 학습 에서 사용했던 예시 데이터셋에서 모든 특성이 관계를 맺고 있다면 몇 개의 파라미터가 필요할까요?
| 하늘 상태 | 온도 | 습도 | 바람 | 해수 온도 | 일기 예보 | 물놀이를 나갈까? |
|---|---|---|---|---|---|---|
| 맑음 | 따듯함 | 보통 | 강함 | 따듯함 | 일정함 | 예 |
| 맑음 | 따듯함 | 높음 | 강함 | 따듯함 | 일정함 | 예 |
| 흐림 | 추움 | 높음 | 강함 | 따듯함 | 가변적 | 아니오 |
| 맑음 | 따듯함 | 높음 | 강함 | 차가움 | 가변적 | 예 |
클래스의 개수 $k = 1$ 이고, 특성의 개수 $d = 6$ 이므로 $2 \cdot (2^6-1) \times (2 - 1) = 126$ 개의 파라미터가 필요하게 됩니다. 모든 특성이 관계를 맺고 있다면 상당히 간단해보이는 데이터셋으로부터 분류 기준을 이끌어 내는 데만도 많은 파라미터를 필요로 하게 됩니다. 실제 데이터는 수십 ~ 수백 개의 특성을 가지고 있는 경우가 많습니다. 특성의 개수에 따라 필요한 파라미터의 개수는 기하급수적으로 늘어나므로 특성 사이의 관계를 어떻게 해결해주지 않으면 필요한 파라미터의 개수는 엄청나게 늘어날 것입니다. 실제로 20개의 특성을 가진 데이터셋이라면 필요한 파라미터의 개수는 100만개가 넘습니다. 이 문제를 해결해줄 조건부 독립에 대해 알아봅시다.
Conditional Independence
조건부 독립(Conditional Independence) 은 특성의 개수를 줄이지 않고도 필요한 파라미터의 개수를 줄일 수 있는 방법입니다. 조건부 독립이 무엇이길래 이런 일을 할 수 있는 것일까요? 조건부 독립은 임의의 관계에 있는 두 사건이 주어진 조건하에서는 독립이 되는 경우를 말합니다. 조건부 독립의 예시를 몇 가지 들어봅시다.
“비가 오는 사건” 과 “천둥이 치는 사건” 이 있다고 해봅시다. 두 사건 사이에는 어떤 관계가 있어 보입니다. 그런데 가운데 “번개가 쳤다” 라는 조건이 주어졌다고 해봅시다. “번개가 쳤다” 라는 조건하에서는 “천둥이 치는 사건” 과 “비가 오는 사건” 은 독립이 되어버립니다. 각각을 확률로 나타내어 보겠습니다. (해당 예시에서 마른 하늘에 번개가 치는 것은 예외로 합니다.)
\[\begin{aligned} P(천둥=침|비=옴) &\neq P(천둥=침)\\ P(천둥=침|비=옴, 번개=침) &= P(천둥=침|번개=침)\\ P(비|천둥=침, 번개=침) &= P(비=옴|번개=침)\\ \because P(천둥=침, 비|번개=침) &= P(천둥=침|번개=침)P(비=옴|번개=침) \end{aligned}\]천둥과 비는 독립이 아니므로 비가 왔을 때 천둥이 칠 확률 $P(천둥 \vert 비)$ 와 아무런 조건이 없을 때 천둥이 칠 확률 $P(천둥)$ 은 같지 않습니다. 비가 올 때 천둥이 칠 확률이 훨씬 높겠지요. 하지만 번개라는 조건이 주어지면 다른 두 사건은 이 조건에
두 번째 예시는 그림과 함께 알아봅시다. 아래 그림은 지휘관과 지휘관의 명령을 따르는 직원 A,B 를 그림으로 나타낸 것입니다.

이미지 출처 : 인공지능 및 기계학습 개론 학습자료
먼저 A가 지휘관의 명령을 듣지 못하는 상태, 즉 지휘관의 명령을 알 수 없는 상태라고 가정해 봅시다. 이 경우에는 B가 앞으로 가는 것을 보았을 때와 그렇지 않을 때 A가 앞으로 갈 확률은 다를 것입니다. 아무래도 B가 앞으로 가는 것을 본다면 ‘지휘관이 B에게 명령을 내렸겠구나’라고 생각하고 앞으로 가게 되겠지요. 수식으로는 아래와 같이 나타낼 수 있습니다.
\[P(\text{OfficerA=Go} \vert \text{OfficerB=Go}) \neq P(\text{OfficerA=Go})\]이번에는 A가 지휘관의 명령을 들을 수 있는 상태라고 가정하고 같은 상황에 대한 확률을 구해봅시다. 지휘관의 명령을 들을 수 있다면 B가 앞으로 가든 말든 A가 앞으로 갈 확률에는 차이가 없습니다. B가 앞으로 가든지 말든지 지휘관의 명령만 따라서 움직이면 되기 때문입니다.
\[P(\text{OfficerA=Go} \vert \text{OfficerB=Go, Commander = Go}) = P(\text{OfficerA=Go} \vert \text{Commander=Go})\]이렇게 독립이 아닌 두 사건에 대해 특정 조건이 개입했을 때 조건부 확률이 독립이 되는 관계를 조건부 독립이라고 합니다. 조건 $y$ 에 대하여 조건부 독립인 사건 $x_1, \cdots, x_n$ 은 다음과 같은 수식을 만족합니다.
\[( \forall x_1, x_2,y) \\ \begin{aligned} P(x_1 \vert x_2, y) &= P(x_1 \vert y) \\ \therefore P(x_1,x_2 \vert y) &= P(x_1 \vert y)P(x_2 \vert y) \end{aligned}\]마지막 등식을 사용하여 Class conditional density의 항을 다음과 같이 변형할 수 있습니다.
\[P(X= \{x_1, ..., x_d\} \vert Y=y) \rightarrow \prod^d_{i=1} P(X_i = x_i \vert Y=y)\]Naive Bayes Classifier
베이즈 분류기를 수식으로 나타낸 $f^*$ 에 변형된 수식을 적용해봅시다.
\[\begin{aligned} f^* &= \text{argmax}_{Y=y} P(X = x \vert Y = y) P(Y = y) \\ &\approx \text{argmax}_{Y=y} P(Y = y) \prod_{1 \leq i \leq d} P(X_i = x_i \vert Y=y) \end{aligned}\]특성 $x_1, … ,x_d$ 가 모두 관계를 맺고 있을 때 Class conditional density 항을 구하기 위해서 필요한 파라미터의 개수는 $(2^d-1)k$ 였습니다. 식을 변형한 후에는 어떻게 될까요? 변형한 식에서 Class conditional density 부분을 구하기 위해 필요한 파라미터의 개수는 $d \cdot k$ 개가 됩니다. 위에서 했던 것처럼 특성이 $6$ 개, 클래스가 $2$ 개인 분류 문제를 위해서 필요한 파라미터의 개수를 구해봅시다. Class prior 항을 구하기 위해 필요한 파라미터의 개수는 $k-1$ 로 동일하므로 $6 \cdot 2 \times 1 = 12$ 개가 됩니다. 훨씬 더 줄어든 것을 볼 수 있습니다.
하지만 현실세계에서는 특성들이 서로 조건부독립을 만족하지 않는 경우가 대부분입니다. 파라미터의 개수를 줄이기 위한 가정이 말 그대로 너무 순진한(Naive, 나이브) 한 가정이기 때문에 이 가정을 사용한 베이즈 분류기를 나이브 베이즈 분류기(Naive Bayes Classifier) 라고 부릅니다. 나이브 베이즈 분류기는 비록 특수한 가정을 사용하였지만 몇몇 태스크에서 다른 복잡한 모델보다도 더 좋은 성능을 내기도 합니다.

Comments