규칙 기반 학습 (Rule Based Learning)
05 Apr 2020 | Machine-Learning
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 강의를 바탕으로 작성하였습니다.
Rule Based Learning
머신러닝이란 무엇일까요? 위키백과로부터 머신러닝의 정의를 가져와 봅시다.
” 기계 학습 또는 머신 러닝(Machine learning)은 경험을 통해 자동으로 개선하는 컴퓨터 알고리즘의 연구이다. 인공지능의 한 분야로 간주된다. 컴퓨터가 학습할 수 있도록 하는 알고리즘과 기술을 개발하는 분야이다.”
위에 설명되어 있는 것처럼 머신러닝을 수행하기 위해서 컴퓨터는 많은 경험을 학습합니다. 그리고 학습된 경험을 바탕으로 알고리즘을 만들어 특정한 일(Task)을 수행하지요. 중요한 것은 컴퓨터가 학습을 통해 만드는 알고리즘의 성능은 얼마나 많은 경험(데이터)을 수집하여 학습했는지에 달렸다는 것입니다.
사람이 지식을 습득하는 방법 중 하나도 위와 유사합니다. 흔히 사용하는 관용어 중에 “실패를 통해 배운다” 라는 말이 있습니다. 어떤 일을 성공시키기 위해서 무엇을 해야 할 지, 또는 하지 말아야 할 지를 많은 경험을 통해 배울 때 이 말을 사용합니다. 하지 말아야 할 일은 한 경우에는 실패하게 되고, 해야 할 일을 하지 않은 경우에도 실패하게 되지요. 반대로 해야할 일을 하고, 하지 말아야 할 일은 하지 않으면 성공합니다. 이를 경험을 통한 시행착오를 통해 배우지요.
이번 게시물에서는 머신러닝의 가장 기초적인 방법 중 하나인 규칙 기반 학습(Rule Based Learning) 에 대해 배워보도록 하겠습니다.
Rule Based Learning (규칙 기반 학습)
이후에 이루어질 논의를 더 쉽게 하기 위해서 몇 가지 가정을 해야합니다. 첫 번째로 우리가 알아볼 세상에서는 관측 오차(Observation errors)가 없습니다. 두 번째로 일관성이 없는 관측(Inconsistent observations)도 없습니다. 세 번째로 어떤 확률론적 요소(Stochastic element)도 없습니다. 마지막으로는 우리가 관측하는 정보가 시스템에 있는 모든 정보입니다. 이 가정을 모두 만족하는 곳을 완벽한 세계(Perfect world) 라고 합니다.
이 완벽한 세계에서 관측한 아래와 같은 데이터가 있다고 해봅시다.
하늘 상태
온도
습도
바람
해수 온도
일기 예보
물놀이를 나갈까?
맑음
따듯함
보통
강함
따듯함
일정함
예
맑음
따듯함
높음
강함
따듯함
일정함
예
흐림
추움
높음
강함
따듯함
가변적
아니오
맑음
따듯함
높음
강함
차가움
가변적
예
앞으로 머신러닝에서 등장할 데이터는 일반적으로 위와 같이 생겼습니다. 우리의 목적은 위와 같이 관측된 데이터로부터 더 좋은 근사 함수를 생성하는 것입니다. 아래는 위 표의 요소를 설명하기 위한 용어들입니다.
가장 먼저 알아야 할 용어는 인스턴스(Instance) 입니다. 위 표에서 각 행(Row)이 인스턴스입니다. 일반적으로 특성(Feature)과 레이블(Label)로 이루어져 있습니다. 위 표에서 (하늘 상태, 온도, 습도, 바람, 해수 온도, 일기예보) 를 특성이라고 하고 그 값에 해당하는 (맑음, 따듯함, 보통, 강함, 따듯함, 일정함) 을 특성값이라고 합니다. 그에 따라 결정되는 (물놀이를 나갈까?) 와 그 값은 레이블이라고 합니다.
가설(Hypothesis) 에 대해서도 알아야 합니다. 가설은 특성값으로부터 특정 레이블을 도출할 가능성이 있는 함수입니다. 위 데이터셋에서 도출할 수 있는 가설은 다음과 같습니다.
$h_0$ : (맑음, 따듯함, ?, ?, ?, ?) $\rightarrow$ 예
위 가설에서 (습도, 바람, 해수온도, 일기예보) 가 ”?” 로 표시된 이유는 주어진 데이터셋을 통해서 도출해낼 수 없기 때문입니다. 습도의 경우 인스턴스에서 2와 3에서 모두 “높음” 이지만 2번 인스턴스의 레이블은 “예”, 3번 인스턴스의 레이블은 “아니오” 입니다. 이렇게 주어진 데이터셋 만으로는 해당 특성값이 레이블에 어떤 영향을 미치는지 알 수 없기 때문에 ”?” 로 표시합니다. 이렇게 결정되지 않은 특성 때문에 여러 종류의 가설이 가능합니다. 데이터를 더욱 많이 수집하여 여러 가설로부터 하나의 목적 함수(Target function) 을 찾는 것이 우리의 목적이라 할 수 있겠습니다.
이번에는 관측한 데이터의 개수에 따라 가설이 어떻게 변화하는지 알아봅시다. 위 표에서 1, 2, 3번 인스턴스를 관측하여 도출한 가설 $h_1$ 은 (맑음, 따듯함, ?, ?, ?, 일정함) $\rightarrow$ “예” 입니다. 결정되지 않은 특성이 3개인 것을 알 수 있습니다. 1, 2번 인스턴스만 관찰한 뒤에 가설을 세워봅시다. 이 때의 가설 $h_2$ 는 (맑음, 따듯함, ?, 강함, 따듯함, 일정함) $\rightarrow$ “예” 입니다. 2, 3번 인스턴스를 관찰한 뒤 가설을 세워보면 어떻게 나올까요? 이 가설 $h_3$ 는 (맑음, 따듯함, 보통, ?, ?, 일정함) $\rightarrow$ “예” 입니다.
앞서 4개의(1, 2, 3, 4번) 인스턴스를 모두 관측하여 나타낸 가설 $h_0$ 에서는 결정되지 않은 특성, 즉 ”?” 로 나타난 특성이 4개가 있었습니다. 그리고 3개의 인스턴스를 관측하여 나타낸 가설 $h_1$ 에서는 ”?” 인 특성이 3개가 있었습니다. 2개의 인스턴스를 관측했을 때는 가설 $h_2, h_3$ 에 “?” 가 각각 1번, 2번씩 등장했습니다.
가설들 중 $h_0, h_1$ 은 상대적으로 여러 인스턴스로부터 도출된 일반적(General) 인 가설입니다. 관측된 데이터셋에 있는 인스턴스 말고도 해당 가설을 만족하는 인스턴스가 더 많을 수 있기 때문이지요. 반대로 $h_2, h_3$ 는 상대적으로 특수한(Specific) 가설입니다. 특히 $h_2$ 같이 결정되지 않은 특성( ”?” )이 하나인 경우에는 2번과 3번 인스턴스 이외에 가설을 만족하는 다른 인스턴스가 없습니다.
상대적으로 일반적인 가설과 특수한 가설 중 어떤 것이 더 좋은 것일까요? 위에서 보았던 위키백과 머신러닝 페이지로 돌아가봅시다. 위에서 인용했던 머신러닝의 정의 뒷부분에는 다음과 같은 말이 써있습니다.
“기계 학습의 핵심은 표현(representation)과 일반화(generalization)에 있다. 표현이란 데이터의 평가이며, 일반화란 아직 알 수 없는 데이터에 대한 처리이다.”
위의 인용 부분으로부터 상대적으로 일반적인 가설이 더 좋은 것을 알 수 있습니다. 특수한 가설이 좋지 않은 이유는 그것이 관측되지 않은 데이터를 만족시킬 수 없기 때문이지요. 아무튼 더 일반적인 가설을 만들어 내기 위해서 더 많은 데이터를 관측해야 합니다. 아래부터는 가설을 찾아나가기 위한 규칙 기반 학습 알고리즘에 대해 알아봅니다.
Find-S Algorithm & Version Space
Find-S Algorithm 은 특수한 가설로부터 일반적인 가설로 가설의 범위를 확장해나가는 알고리즘입니다. 이 알고리즘은 아무런 특성도 한정되지 않은 영가설(Null hypothesis)로부터 시작합니다. 그리고 Positive한 레이블을 나타내는 인스턴스 하나씩을 골라 해당하는 특성을 기존의 가설과 비교하며 판단해나갑니다. 기존의 가설과 새로운 인스턴스의 특성값이 다를 경우 이 경우를 포함시키며 가설의 범위를 확장해 나갑니다. 예시를 위해 위에서 사용했던 표를 다시 인용해봅시다.
하늘 상태
온도
습도
바람
해수 온도
일기예보
물놀이를 나갈까?
맑음
따듯함
보통
강함
따듯함
일정함
예
맑음
따듯함
높음
강함
따듯함
일정함
예
흐림
추움
높음
강함
따듯함
가변적
아니오
맑음
따듯함
높음
강함
차가움
가변적
예

이미지 출처 : aistudy.com
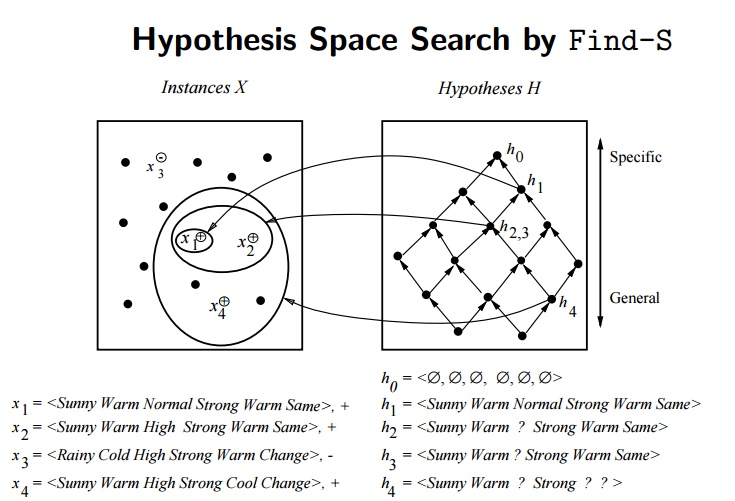
위 표에서 Positive한 레이블을 나타내는 인스턴스는 1, 2, 4번 인스턴스 입니다. 이 세 인스턴스를 사용하여 Find-S Algorithm 과정을 진행해봅시다. 맨 처음은 영가설인 $h_0 = (\phi, \phi, \phi, \phi, \phi, \phi)$ 에서 시작합니다. 새로운 인스턴스 1번에 의해 정해지는 가설 $h_1$ 은 (맑음, 따듯함, 보통, 강함, 따듯함, 일정함) 입니다. 이 가설에 새로운 인스턴스 2번을 적용하면 새로운 가설 $h_2$ 는 (맑음, 따듯함, ?, 강함, 따듯함, 일정함) 으로 변하게 됩니다. “습도” 특성에 해당하는 가설이 변경되며 가설의 범위가 확장되는 것을 볼 수 있습니다. 마지막으로 4번 인스턴스를 추가로 적용하여 최종적으로 도출되는 가설 $h_3$ 은 (맑음, 따듯함, ?, 강함, ?, ?) 이 됩니다.
이미지 출처 : excelsior-cjh.tistory.com
이 과정에서 생성가능한 모든 가설의 수를 모아둔 집합을 버전 공간(Version Space, VS) 이라고 합니다. 버전 공간에는 가장 일반적인 가설을 나타내는 경계 $G$ 와 가장 특수한 가설을 나타내는 경계 $S$ 가 있습니다. 두 경계를 수식으로는 아래와 같이 나타낼 수 있습니다.
\[VS_{H,D} = \{h \in H \vert \quad \exists s \in S, \exists g \in G, \quad g \geq h \geq s \}\]

이미지 출처 : aistudy.com
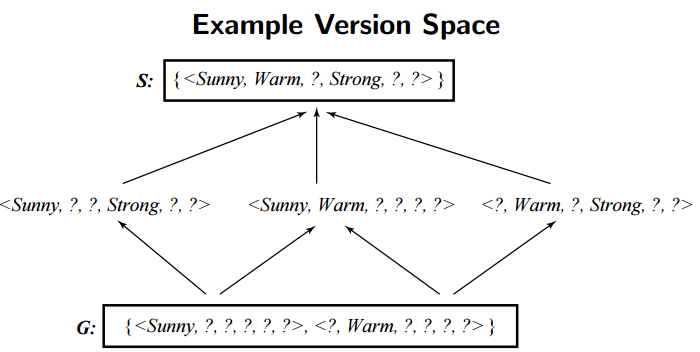
위에서 알아 본 것처럼 4개의 데이터셋으로부터 Find-S Algorithm을 통해 구할 수 있는 특수한 경계 $S$ 는 (맑음, 따듯함, ?, 강함, ?, ?) 입니다. 그리고 가장 일반적인 경계 $G$ 로는 {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?)} 이 있습니다. 이 사이에는 (맑음, ?, ?, 강함, ?, ?), (맑음, 따듯함, ?, ?, ?, ?), (?, 따듯함, ?, 강함, ?, ?) 등의 많은 가설이 존재할 수 있습니다.
이미지 출처 : excelsior-cjh.tistory.com
Find-S 알고리즘은 너무 특수한 가설에 빠질 경우 이를 개선할 수 있는 역추적 방식을 제공하지 않는다는 단점을 가지고 있습니다. 그렇다면 Find-S 알고리즘 이외에 버전 공간(Version space)을 구하는 다른 방법은 없을까요?
후보 제거 알고리즘(Candidate Elimination Algorithm)
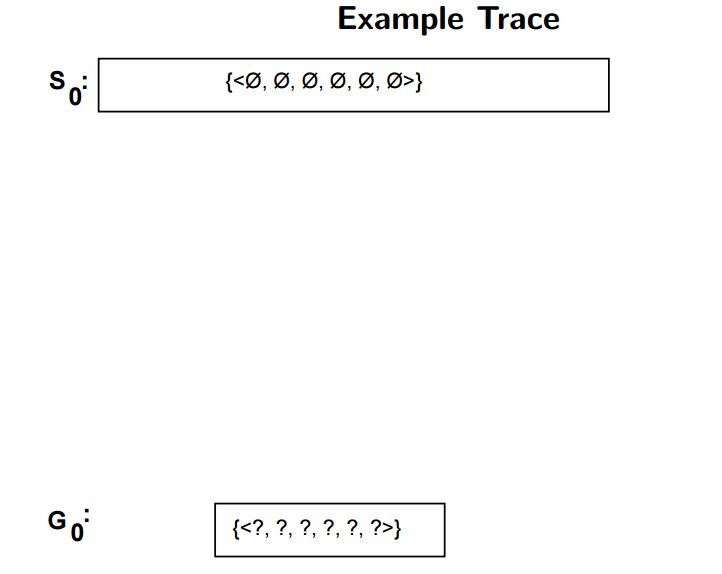
후보 제거 알고리즘(Candidate Elimination Algorithm) 은 버전 공간을 구하기 위한 또 다른 알고리즘입니다. 이 알고리즘은 가장 특수한(Specific)한 가설 $S_0 = (\phi, \phi, \phi, \phi, \phi, \phi)$ 와 가장 일반적인 가설 $G_0 = (?, ?, ?, ?, ?, ?)$ 로부터 시작하게 됩니다. 후보 제거 알고리즘도 Find-S 알고리즘과 마찬가지로 인스턴스 하나씩을 적용하여 두 가설 사이에 존재하는 후보 가설들을 줄여나갑니다. Find-S 알고리즘에서는 Positive한 인스턴스만을 사용하여 일반화했지만 후보 제거 알고리즘은 Positive한 인스턴스와 Negative한 인스턴스 2가지를 모두 사용합니다.
이미지 출처 : excelsior-cjh.tistory.com
후보 제거 알고리즘이 진행되는 과정을 살펴봅시다. 새로 적용할 인스턴스의 레이블이 Positive하면 이 인스턴스를 만족시킬 수 있을 만큼만 특수 경계인 $S$ 를 일반화 해나갑니다. 이 과정에서 일반 경계인 $G$ 에 어긋나는 가설이 있을 경우에는 해당 조건을 제거합니다. 반대로 새로 적용할 인스턴스의 레이블이 Negative이면 이 인스턴스가 Negative로 분류될 수 있도록 일반 경계 $G$ 의 범위를 줄여나갑니다. 이 과정에서도 $S$ 쪽에 새로 적용되는 인스턴스를 만족시키는 조건이 있다면 이 조건을 탈락시킵니다. 말로만 설명하니 이해하기가 어렵습니다. 위에서 사용했던 표를 다시 가져와서 후보 제거 알고리즘을 적용해봅시다.
하늘 상태
온도
습도
바람
해수 온도
일기 예보
물놀이를 나갈까?
맑음
따듯함
보통
강함
따듯함
일정함
예
맑음
따듯함
높음
강함
따듯함
일정함
예
흐림
추움
높음
강함
따듯함
가변적
아니오
맑음
따듯함
높음
강함
차가움
가변적
예
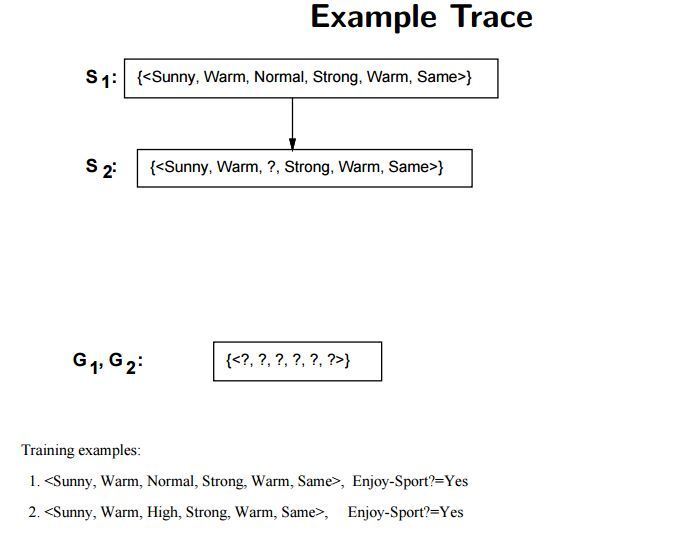
첫 번째 인스턴스를 적용했을 때의 각 경계는 다음과 같이 변하게 됩니다. $S_1 = (맑음, 따듯함, 보통, 강함, 따듯함, 일정함), G_1 = (?, ?, ?, ?, ?, ?)$ 첫 번째 인스턴스의 레이블이 “예” 이므로 이에 맞게 $S$ 를 조정하고 $G$ 는 거스르는 부분이 없으므로 그대로 유지합니다.
두 번째 인스턴스를 적용하면 $S_2 = (맑음, 따듯함, ?, 강함, 따듯함, 일정함)$, $G_2 = (?, ?, ?, ?, ?, ?)$ 이 됩니다. 앞선 과정과 동일하며 여기까지는 Find-S 알고리즘과도 유사합니다. 첫 번째와 두 번째 인스턴스 모두 Positive 하므로 $S$ 만 점점 General 해지는 것을 볼 수 있습니다.
이미지 출처 : excelsior-cjh.tistory.com
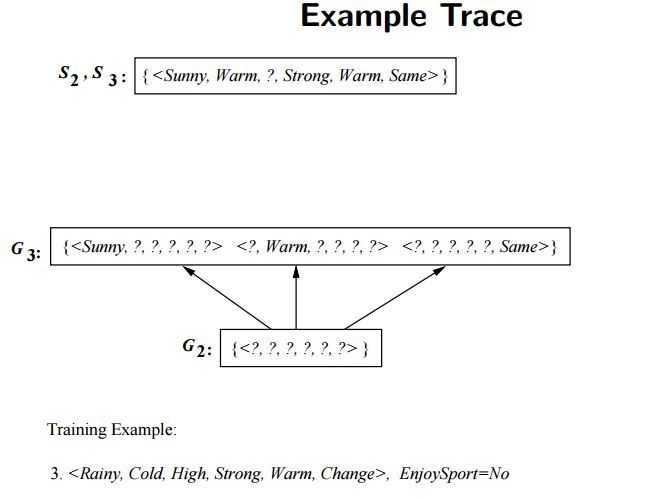
이번에는 세 번째 인스턴스를 적용해봅시다. 여기서 Find-S 알고리즘과의 차이가 발생합니다. Find-S 알고리즘에서는 레이블링이 “아니오” 인 인스턴스는 적용하지 않았기 때문입니다. 세 번째 인스턴스를 적용하여 변한 가설은 $S_3 = (맑음, 따듯함, ?, 강함, 따듯함, 일정함), G_3 = {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?), (?, ?, ?, ?, ?, 일정함)}$ 입니다. 앞선 두 인스턴스와 세 번째 인스턴스는 “하늘 상태, 온도, 일기 예보” 세 가지 특성에서 다른 값을 나타냅니다. 각 특성들에서 세 번째 인스턴스 특성값은 “흐림, 추움, 가변적” 입니다. 이와 반대되는 특성값으로 이루어진 가설을 각각 $G$ 에 추가해주면 위와 같이 $G_3 = {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?), (?, ?, ?, ?, ?, 일정함)}$ 를 나타내게 됩니다.
이미지 출처 : excelsior-cjh.tistory.com
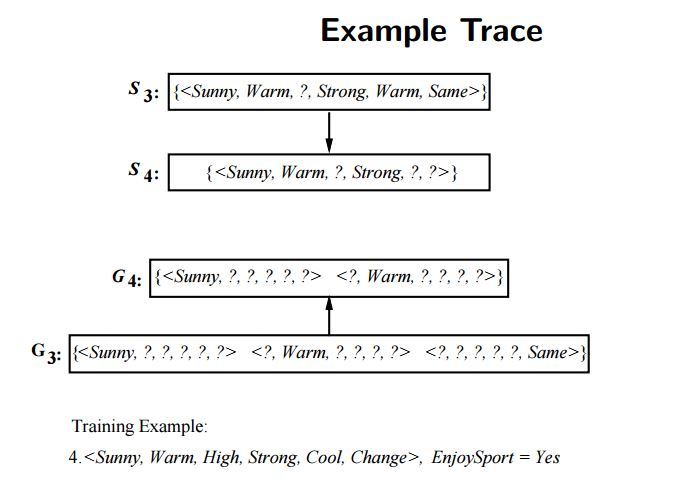
마지막으로 네 번째 인스턴스를 적용하여 가설을 개선해봅시다. 개선된 가설은 $S_4 = (맑음, 따듯함, ?, 강함, ?, ?), G_4 = {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?)}$ 입니다. 먼저 $S$ 쪽은 “해수 온도” 와 “일기 예보” 에서 기존 가설과 네 번째 인스턴스의 특성값이 다르므로 ”?” 로 처리해주어 일반화합니다. 그리고 $G$ 쪽은 네 번째 인스턴스에서 “일기 예보” 의 특성값이 “가변적” 임에도 레이블이 “예” 이므로 $(?, ?, ?, ?, ?, 일정함)$ 에 해당하는 가설을 탈락시킵니다.
이미지 출처 : excelsior-cjh.tistory.com
이렇게 도출된 버전 공간을 다른 데이터에 적용하면 어떻게 될까요? 아래 표는 레이블링이 되어있지 않은 추가 데이터셋입니다. 4개의 인스턴스에 후보 제거 알고리즘을 적용하여 도출된 버전 공간을 통해 아래 데이터를 레이블링해 봅시다.
하늘 상태
온도
습도
바람
해수 온도
일기 예보
물놀이를 나갈까?
맑음
따듯함
보통
강함
차가움
가변적
?
흐림
추움
높음
약함
따듯함
일정함
?
흐림
따듯함
보통
강함
따듯함
일정함
?
위 표에서 첫 번째와 두 번째 인스턴스는 위에서 도출한 버전 공간 바깥에 위치하기 때문에 레이블을 결정할 수 있습니다. 첫 번째 인스턴스의 경우 $S_4 = (맑음, 따듯함, ?, 강함, ?, ?)$ 를 모두 만족시키므로 “예” 로 레이블링 할 수 있습니다. 두 번째 인스턴스는 $G_4 = {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?)}$ 중 어느 것도 만족시키고 있지 않으므로 “아니오” 로 레이블링하면 됩니다.
하지만 마지막 인스턴스는 버전 공간인 $S_4, G_4$ 사이에 위치합니다. 이 경우에는 함부로 레이블을 결정할 수가 없습니다. 이런 문제를 해결하기 위해서는 어떻게 해야 할까요?
정답은 데이터의 수를 늘리는 것입니다. 완벽한 세계(Perfect world)에서는 데이터가 늘어나게 되면 후보 제거 알고리즘을 통해서 버전 공간(Version space)을 점점 줄여나갈 수 있습니다. 더욱 많아진다면 하나의 가설로 축소할 수도 있지요. 하지만 현실세계에서는 모든 관측 데이터에 소음이 존재하고 우리가 관측하지 못하는 특성이 개입될 수도 있습니다. 이 때문에 후보 제거 알고리즘 등의 규칙 기반 방식으로는 현실에서 일어나는 모든 데이터에 대한 설명력이 떨어지게 됩니다.
본 포스트는 문일철 교수님의 인공지능 및 기계학습 개론 I 강의를 바탕으로 작성하였습니다.
Rule Based Learning
머신러닝이란 무엇일까요? 위키백과로부터 머신러닝의 정의를 가져와 봅시다.
” 기계 학습 또는 머신 러닝(Machine learning)은 경험을 통해 자동으로 개선하는 컴퓨터 알고리즘의 연구이다. 인공지능의 한 분야로 간주된다. 컴퓨터가 학습할 수 있도록 하는 알고리즘과 기술을 개발하는 분야이다.”
위에 설명되어 있는 것처럼 머신러닝을 수행하기 위해서 컴퓨터는 많은 경험을 학습합니다. 그리고 학습된 경험을 바탕으로 알고리즘을 만들어 특정한 일(Task)을 수행하지요. 중요한 것은 컴퓨터가 학습을 통해 만드는 알고리즘의 성능은 얼마나 많은 경험(데이터)을 수집하여 학습했는지에 달렸다는 것입니다.
사람이 지식을 습득하는 방법 중 하나도 위와 유사합니다. 흔히 사용하는 관용어 중에 “실패를 통해 배운다” 라는 말이 있습니다. 어떤 일을 성공시키기 위해서 무엇을 해야 할 지, 또는 하지 말아야 할 지를 많은 경험을 통해 배울 때 이 말을 사용합니다. 하지 말아야 할 일은 한 경우에는 실패하게 되고, 해야 할 일을 하지 않은 경우에도 실패하게 되지요. 반대로 해야할 일을 하고, 하지 말아야 할 일은 하지 않으면 성공합니다. 이를 경험을 통한 시행착오를 통해 배우지요.
이번 게시물에서는 머신러닝의 가장 기초적인 방법 중 하나인 규칙 기반 학습(Rule Based Learning) 에 대해 배워보도록 하겠습니다.
Rule Based Learning (규칙 기반 학습)
이후에 이루어질 논의를 더 쉽게 하기 위해서 몇 가지 가정을 해야합니다. 첫 번째로 우리가 알아볼 세상에서는 관측 오차(Observation errors)가 없습니다. 두 번째로 일관성이 없는 관측(Inconsistent observations)도 없습니다. 세 번째로 어떤 확률론적 요소(Stochastic element)도 없습니다. 마지막으로는 우리가 관측하는 정보가 시스템에 있는 모든 정보입니다. 이 가정을 모두 만족하는 곳을 완벽한 세계(Perfect world) 라고 합니다.
이 완벽한 세계에서 관측한 아래와 같은 데이터가 있다고 해봅시다.
| 하늘 상태 | 온도 | 습도 | 바람 | 해수 온도 | 일기 예보 | 물놀이를 나갈까? |
|---|---|---|---|---|---|---|
| 맑음 | 따듯함 | 보통 | 강함 | 따듯함 | 일정함 | 예 |
| 맑음 | 따듯함 | 높음 | 강함 | 따듯함 | 일정함 | 예 |
| 흐림 | 추움 | 높음 | 강함 | 따듯함 | 가변적 | 아니오 |
| 맑음 | 따듯함 | 높음 | 강함 | 차가움 | 가변적 | 예 |
앞으로 머신러닝에서 등장할 데이터는 일반적으로 위와 같이 생겼습니다. 우리의 목적은 위와 같이 관측된 데이터로부터 더 좋은 근사 함수를 생성하는 것입니다. 아래는 위 표의 요소를 설명하기 위한 용어들입니다.
가장 먼저 알아야 할 용어는 인스턴스(Instance) 입니다. 위 표에서 각 행(Row)이 인스턴스입니다. 일반적으로 특성(Feature)과 레이블(Label)로 이루어져 있습니다. 위 표에서 (하늘 상태, 온도, 습도, 바람, 해수 온도, 일기예보) 를 특성이라고 하고 그 값에 해당하는 (맑음, 따듯함, 보통, 강함, 따듯함, 일정함) 을 특성값이라고 합니다. 그에 따라 결정되는 (물놀이를 나갈까?) 와 그 값은 레이블이라고 합니다.
가설(Hypothesis) 에 대해서도 알아야 합니다. 가설은 특성값으로부터 특정 레이블을 도출할 가능성이 있는 함수입니다. 위 데이터셋에서 도출할 수 있는 가설은 다음과 같습니다.
$h_0$ : (맑음, 따듯함, ?, ?, ?, ?) $\rightarrow$ 예
위 가설에서 (습도, 바람, 해수온도, 일기예보) 가 ”?” 로 표시된 이유는 주어진 데이터셋을 통해서 도출해낼 수 없기 때문입니다. 습도의 경우 인스턴스에서 2와 3에서 모두 “높음” 이지만 2번 인스턴스의 레이블은 “예”, 3번 인스턴스의 레이블은 “아니오” 입니다. 이렇게 주어진 데이터셋 만으로는 해당 특성값이 레이블에 어떤 영향을 미치는지 알 수 없기 때문에 ”?” 로 표시합니다. 이렇게 결정되지 않은 특성 때문에 여러 종류의 가설이 가능합니다. 데이터를 더욱 많이 수집하여 여러 가설로부터 하나의 목적 함수(Target function) 을 찾는 것이 우리의 목적이라 할 수 있겠습니다.
이번에는 관측한 데이터의 개수에 따라 가설이 어떻게 변화하는지 알아봅시다. 위 표에서 1, 2, 3번 인스턴스를 관측하여 도출한 가설 $h_1$ 은 (맑음, 따듯함, ?, ?, ?, 일정함) $\rightarrow$ “예” 입니다. 결정되지 않은 특성이 3개인 것을 알 수 있습니다. 1, 2번 인스턴스만 관찰한 뒤에 가설을 세워봅시다. 이 때의 가설 $h_2$ 는 (맑음, 따듯함, ?, 강함, 따듯함, 일정함) $\rightarrow$ “예” 입니다. 2, 3번 인스턴스를 관찰한 뒤 가설을 세워보면 어떻게 나올까요? 이 가설 $h_3$ 는 (맑음, 따듯함, 보통, ?, ?, 일정함) $\rightarrow$ “예” 입니다.
앞서 4개의(1, 2, 3, 4번) 인스턴스를 모두 관측하여 나타낸 가설 $h_0$ 에서는 결정되지 않은 특성, 즉 ”?” 로 나타난 특성이 4개가 있었습니다. 그리고 3개의 인스턴스를 관측하여 나타낸 가설 $h_1$ 에서는 ”?” 인 특성이 3개가 있었습니다. 2개의 인스턴스를 관측했을 때는 가설 $h_2, h_3$ 에 “?” 가 각각 1번, 2번씩 등장했습니다.
가설들 중 $h_0, h_1$ 은 상대적으로 여러 인스턴스로부터 도출된 일반적(General) 인 가설입니다. 관측된 데이터셋에 있는 인스턴스 말고도 해당 가설을 만족하는 인스턴스가 더 많을 수 있기 때문이지요. 반대로 $h_2, h_3$ 는 상대적으로 특수한(Specific) 가설입니다. 특히 $h_2$ 같이 결정되지 않은 특성( ”?” )이 하나인 경우에는 2번과 3번 인스턴스 이외에 가설을 만족하는 다른 인스턴스가 없습니다.
상대적으로 일반적인 가설과 특수한 가설 중 어떤 것이 더 좋은 것일까요? 위에서 보았던 위키백과 머신러닝 페이지로 돌아가봅시다. 위에서 인용했던 머신러닝의 정의 뒷부분에는 다음과 같은 말이 써있습니다.
“기계 학습의 핵심은 표현(representation)과 일반화(generalization)에 있다. 표현이란 데이터의 평가이며, 일반화란 아직 알 수 없는 데이터에 대한 처리이다.”
위의 인용 부분으로부터 상대적으로 일반적인 가설이 더 좋은 것을 알 수 있습니다. 특수한 가설이 좋지 않은 이유는 그것이 관측되지 않은 데이터를 만족시킬 수 없기 때문이지요. 아무튼 더 일반적인 가설을 만들어 내기 위해서 더 많은 데이터를 관측해야 합니다. 아래부터는 가설을 찾아나가기 위한 규칙 기반 학습 알고리즘에 대해 알아봅니다.
Find-S Algorithm & Version Space
Find-S Algorithm 은 특수한 가설로부터 일반적인 가설로 가설의 범위를 확장해나가는 알고리즘입니다. 이 알고리즘은 아무런 특성도 한정되지 않은 영가설(Null hypothesis)로부터 시작합니다. 그리고 Positive한 레이블을 나타내는 인스턴스 하나씩을 골라 해당하는 특성을 기존의 가설과 비교하며 판단해나갑니다. 기존의 가설과 새로운 인스턴스의 특성값이 다를 경우 이 경우를 포함시키며 가설의 범위를 확장해 나갑니다. 예시를 위해 위에서 사용했던 표를 다시 인용해봅시다.
| 하늘 상태 | 온도 | 습도 | 바람 | 해수 온도 | 일기예보 | 물놀이를 나갈까? |
|---|---|---|---|---|---|---|
| 맑음 | 따듯함 | 보통 | 강함 | 따듯함 | 일정함 | 예 |
| 맑음 | 따듯함 | 높음 | 강함 | 따듯함 | 일정함 | 예 |
| 흐림 | 추움 | 높음 | 강함 | 따듯함 | 가변적 | 아니오 |
| 맑음 | 따듯함 | 높음 | 강함 | 차가움 | 가변적 | 예 |

이미지 출처 : aistudy.com
위 표에서 Positive한 레이블을 나타내는 인스턴스는 1, 2, 4번 인스턴스 입니다. 이 세 인스턴스를 사용하여 Find-S Algorithm 과정을 진행해봅시다. 맨 처음은 영가설인 $h_0 = (\phi, \phi, \phi, \phi, \phi, \phi)$ 에서 시작합니다. 새로운 인스턴스 1번에 의해 정해지는 가설 $h_1$ 은 (맑음, 따듯함, 보통, 강함, 따듯함, 일정함) 입니다. 이 가설에 새로운 인스턴스 2번을 적용하면 새로운 가설 $h_2$ 는 (맑음, 따듯함, ?, 강함, 따듯함, 일정함) 으로 변하게 됩니다. “습도” 특성에 해당하는 가설이 변경되며 가설의 범위가 확장되는 것을 볼 수 있습니다. 마지막으로 4번 인스턴스를 추가로 적용하여 최종적으로 도출되는 가설 $h_3$ 은 (맑음, 따듯함, ?, 강함, ?, ?) 이 됩니다.
이미지 출처 : excelsior-cjh.tistory.com
이 과정에서 생성가능한 모든 가설의 수를 모아둔 집합을 버전 공간(Version Space, VS) 이라고 합니다. 버전 공간에는 가장 일반적인 가설을 나타내는 경계 $G$ 와 가장 특수한 가설을 나타내는 경계 $S$ 가 있습니다. 두 경계를 수식으로는 아래와 같이 나타낼 수 있습니다.
\[VS_{H,D} = \{h \in H \vert \quad \exists s \in S, \exists g \in G, \quad g \geq h \geq s \}\]
이미지 출처 : aistudy.com
위에서 알아 본 것처럼 4개의 데이터셋으로부터 Find-S Algorithm을 통해 구할 수 있는 특수한 경계 $S$ 는 (맑음, 따듯함, ?, 강함, ?, ?) 입니다. 그리고 가장 일반적인 경계 $G$ 로는 {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?)} 이 있습니다. 이 사이에는 (맑음, ?, ?, 강함, ?, ?), (맑음, 따듯함, ?, ?, ?, ?), (?, 따듯함, ?, 강함, ?, ?) 등의 많은 가설이 존재할 수 있습니다.
이미지 출처 : excelsior-cjh.tistory.com
Find-S 알고리즘은 너무 특수한 가설에 빠질 경우 이를 개선할 수 있는 역추적 방식을 제공하지 않는다는 단점을 가지고 있습니다. 그렇다면 Find-S 알고리즘 이외에 버전 공간(Version space)을 구하는 다른 방법은 없을까요?
후보 제거 알고리즘(Candidate Elimination Algorithm)
후보 제거 알고리즘(Candidate Elimination Algorithm) 은 버전 공간을 구하기 위한 또 다른 알고리즘입니다. 이 알고리즘은 가장 특수한(Specific)한 가설 $S_0 = (\phi, \phi, \phi, \phi, \phi, \phi)$ 와 가장 일반적인 가설 $G_0 = (?, ?, ?, ?, ?, ?)$ 로부터 시작하게 됩니다. 후보 제거 알고리즘도 Find-S 알고리즘과 마찬가지로 인스턴스 하나씩을 적용하여 두 가설 사이에 존재하는 후보 가설들을 줄여나갑니다. Find-S 알고리즘에서는 Positive한 인스턴스만을 사용하여 일반화했지만 후보 제거 알고리즘은 Positive한 인스턴스와 Negative한 인스턴스 2가지를 모두 사용합니다.
이미지 출처 : excelsior-cjh.tistory.com
후보 제거 알고리즘이 진행되는 과정을 살펴봅시다. 새로 적용할 인스턴스의 레이블이 Positive하면 이 인스턴스를 만족시킬 수 있을 만큼만 특수 경계인 $S$ 를 일반화 해나갑니다. 이 과정에서 일반 경계인 $G$ 에 어긋나는 가설이 있을 경우에는 해당 조건을 제거합니다. 반대로 새로 적용할 인스턴스의 레이블이 Negative이면 이 인스턴스가 Negative로 분류될 수 있도록 일반 경계 $G$ 의 범위를 줄여나갑니다. 이 과정에서도 $S$ 쪽에 새로 적용되는 인스턴스를 만족시키는 조건이 있다면 이 조건을 탈락시킵니다. 말로만 설명하니 이해하기가 어렵습니다. 위에서 사용했던 표를 다시 가져와서 후보 제거 알고리즘을 적용해봅시다.
| 하늘 상태 | 온도 | 습도 | 바람 | 해수 온도 | 일기 예보 | 물놀이를 나갈까? |
|---|---|---|---|---|---|---|
| 맑음 | 따듯함 | 보통 | 강함 | 따듯함 | 일정함 | 예 |
| 맑음 | 따듯함 | 높음 | 강함 | 따듯함 | 일정함 | 예 |
| 흐림 | 추움 | 높음 | 강함 | 따듯함 | 가변적 | 아니오 |
| 맑음 | 따듯함 | 높음 | 강함 | 차가움 | 가변적 | 예 |
첫 번째 인스턴스를 적용했을 때의 각 경계는 다음과 같이 변하게 됩니다. $S_1 = (맑음, 따듯함, 보통, 강함, 따듯함, 일정함), G_1 = (?, ?, ?, ?, ?, ?)$ 첫 번째 인스턴스의 레이블이 “예” 이므로 이에 맞게 $S$ 를 조정하고 $G$ 는 거스르는 부분이 없으므로 그대로 유지합니다.
두 번째 인스턴스를 적용하면 $S_2 = (맑음, 따듯함, ?, 강함, 따듯함, 일정함)$, $G_2 = (?, ?, ?, ?, ?, ?)$ 이 됩니다. 앞선 과정과 동일하며 여기까지는 Find-S 알고리즘과도 유사합니다. 첫 번째와 두 번째 인스턴스 모두 Positive 하므로 $S$ 만 점점 General 해지는 것을 볼 수 있습니다.
이미지 출처 : excelsior-cjh.tistory.com
이번에는 세 번째 인스턴스를 적용해봅시다. 여기서 Find-S 알고리즘과의 차이가 발생합니다. Find-S 알고리즘에서는 레이블링이 “아니오” 인 인스턴스는 적용하지 않았기 때문입니다. 세 번째 인스턴스를 적용하여 변한 가설은 $S_3 = (맑음, 따듯함, ?, 강함, 따듯함, 일정함), G_3 = {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?), (?, ?, ?, ?, ?, 일정함)}$ 입니다. 앞선 두 인스턴스와 세 번째 인스턴스는 “하늘 상태, 온도, 일기 예보” 세 가지 특성에서 다른 값을 나타냅니다. 각 특성들에서 세 번째 인스턴스 특성값은 “흐림, 추움, 가변적” 입니다. 이와 반대되는 특성값으로 이루어진 가설을 각각 $G$ 에 추가해주면 위와 같이 $G_3 = {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?), (?, ?, ?, ?, ?, 일정함)}$ 를 나타내게 됩니다.
이미지 출처 : excelsior-cjh.tistory.com
마지막으로 네 번째 인스턴스를 적용하여 가설을 개선해봅시다. 개선된 가설은 $S_4 = (맑음, 따듯함, ?, 강함, ?, ?), G_4 = {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?)}$ 입니다. 먼저 $S$ 쪽은 “해수 온도” 와 “일기 예보” 에서 기존 가설과 네 번째 인스턴스의 특성값이 다르므로 ”?” 로 처리해주어 일반화합니다. 그리고 $G$ 쪽은 네 번째 인스턴스에서 “일기 예보” 의 특성값이 “가변적” 임에도 레이블이 “예” 이므로 $(?, ?, ?, ?, ?, 일정함)$ 에 해당하는 가설을 탈락시킵니다.
이미지 출처 : excelsior-cjh.tistory.com
이렇게 도출된 버전 공간을 다른 데이터에 적용하면 어떻게 될까요? 아래 표는 레이블링이 되어있지 않은 추가 데이터셋입니다. 4개의 인스턴스에 후보 제거 알고리즘을 적용하여 도출된 버전 공간을 통해 아래 데이터를 레이블링해 봅시다.
| 하늘 상태 | 온도 | 습도 | 바람 | 해수 온도 | 일기 예보 | 물놀이를 나갈까? |
|---|---|---|---|---|---|---|
| 맑음 | 따듯함 | 보통 | 강함 | 차가움 | 가변적 | ? |
| 흐림 | 추움 | 높음 | 약함 | 따듯함 | 일정함 | ? |
| 흐림 | 따듯함 | 보통 | 강함 | 따듯함 | 일정함 | ? |
위 표에서 첫 번째와 두 번째 인스턴스는 위에서 도출한 버전 공간 바깥에 위치하기 때문에 레이블을 결정할 수 있습니다. 첫 번째 인스턴스의 경우 $S_4 = (맑음, 따듯함, ?, 강함, ?, ?)$ 를 모두 만족시키므로 “예” 로 레이블링 할 수 있습니다. 두 번째 인스턴스는 $G_4 = {(맑음, ?, ?, ?, ?, ?), (?, 따듯함, ?, ?, ?, ?)}$ 중 어느 것도 만족시키고 있지 않으므로 “아니오” 로 레이블링하면 됩니다.
하지만 마지막 인스턴스는 버전 공간인 $S_4, G_4$ 사이에 위치합니다. 이 경우에는 함부로 레이블을 결정할 수가 없습니다. 이런 문제를 해결하기 위해서는 어떻게 해야 할까요?
정답은 데이터의 수를 늘리는 것입니다. 완벽한 세계(Perfect world)에서는 데이터가 늘어나게 되면 후보 제거 알고리즘을 통해서 버전 공간(Version space)을 점점 줄여나갈 수 있습니다. 더욱 많아진다면 하나의 가설로 축소할 수도 있지요. 하지만 현실세계에서는 모든 관측 데이터에 소음이 존재하고 우리가 관측하지 못하는 특성이 개입될 수도 있습니다. 이 때문에 후보 제거 알고리즘 등의 규칙 기반 방식으로는 현실에서 일어나는 모든 데이터에 대한 설명력이 떨어지게 됩니다.

Comments