사영(Projection)과 정규방정식(Normal Equation)
12 Sep 2020 | Linear-Algebra
Projection
이번 시간에는 사영(Projection)에 대하여 알아보도록 하겠습니다. 위키백과에서는 사영의 뜻을 다음과 같이 서술하고 있습니다.
사영 또는 투영은 어떤 집합을 부분집합으로 특정한 조건을 만족시키면서 옮기는 작용이다.
즉, 벡터의 사영이란 특정 벡터를 다른 벡터 공간으로 옮기는 행위를 말합니다. 벡터의 사영에서 부분공간의 점들 중 거리가 가장 작은 곳으로 옮긴다는 특정 조건이 있습니다. 예를 들어, $\vec{a}$ 를 다른 벡터 $\vec{b}$ 위로 사영하고자 한다면 $\vec{a}$ 가 사영되는 지점인 $\vec{a^\prime}$ 과 원래 벡터 사이의 거리 $\vert\vec{a} - \vec{a^\prime}\vert$ 최소가 됩니다. 아래 그림은 벡터의 사영을 이미지로 나타낸 것입니다.
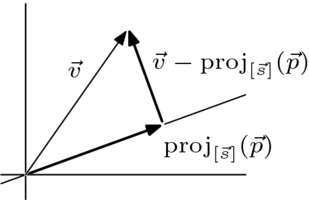
이미지 출처 : wikibooks.org
위 이미지에서 $\vec{v}$ 를 사영한 벡터는 둘 사이의 거리인 $\vert \vec{v} - \text{proj}_{[\vec{s}]}(\vec{p})\vert$를 최소화 하는 지점으로 결정됩니다.
Solve Equation
사영을 이용하면 또 다른 형태의 연립방정식의 해를 구할 수 있습니다. 식의 개수가 미지수의 개수보다 더 많은 경우입니다. 미지수의 개수가 2개이고 식이 3개인 경우를 평면상에 나타내면 아래와 같습니다. 물론, 운좋게 세 직선이 한 점에서 만날 수도 있으나 그런 경우는 제외하겠습니다.

이런 경우에는 정해진 하나의 해가 없습니다. 이 연립방정식을 행렬로 나타냈을 때의 $A$는 열의 개수보다 행의 개수가 많은 행렬이 됩니다. 이럴 때에는 해를 나타내는 벡터 $\vec{b}$ 가 $A$의 Column space 내부에 없기 때문에, $A$의 Column 스페이스와 거리가 최소가 되는 곳, 즉 $\vec{b}$ 를 $A$ 의 Column space로 사영한 곳을 해로 정하게 됩니다. 사영 벡터 $\vec{p} = \hat{c}\cdot A$ 라고 하면 $\vec{b} - \hat{c}\cdot A \perp \vec{a_i}$ 이므로 다음과 같은 식을 만족하게 됩니다.
\[\begin{aligned}
\vec{a_1}^T (\vec{b} - &\hat{c}\cdot A) = 0 \\
\vec{a_2}^T (\vec{b} - &\hat{c}\cdot A) = 0 \\
&\vdots \\
\vec{a_n}^T (\vec{b} - &\hat{c}\cdot A) = 0 \\
\therefore A^T(\vec{b} - &\hat{c}\cdot A) = 0 \\
\end{aligned}\]
식을 전개하여 $\hat{c}$에 대하여 정리하면
\[\hat{c}\cdot A^TA = A^T \cdot\vec{b} \\
\hat{c} = (A^TA)^{-1}A^T \cdot\vec{b}\]
최종적으로 이 해를 구하기 위한 변환 행렬, 즉 사영 행렬(Projection matrix, $P$ )은 다음과 같이 나타낼 수 있습니다.
\[P = A(A^TA)^{-1}A^T \\
\because P\cdot \vec{b} = A \cdot \hat{c} = A(A^TA)^{-1}A^T \cdot\vec{b}\]
$\vec{b}$ 벡터를 어떤 행렬 $A$의 Column space에 사영시키는 간단한 예시를 보겠습니다. 각 행렬과 벡터의 요소는 다음과 같습니다.
\[A = \left[\begin{array}{cc} 1 & 2 \\ 1 & 3 \\ 0 & 0 \end{array} \right] \\ \vec{b} = (4,5,6)^T\]
$A$ 의 Column space는 $xy$ 평면이며, 이 공간으로의 사영시키는 행렬 $P$는 위 식을 사용하여 구할 수 있습니다.
\[A^TA = \left[\begin{array}{ccc} 1 & 1 & 0 \\ 2 & 3 & 0 \end{array} \right]\left[\begin{array}{cc} 1 & 2 \\ 1 & 3 \\ 0 & 0 \end{array} \right] = \left[\begin{array}{cc} 2 & 5 \\ 5 & 13 \end{array} \right] \\
\therefore (A^TA)^{-1} = \left[\begin{array}{cc} 13 & -5 \\ -5 & 2 \end{array} \right]\]
사영 행렬 $P$ 를 구하는 식을 사용하면
\[P = A(A^TA)^{-1}A^T = \left[\begin{array}{cc} 1 & 2 \\ 1 & 3 \\ 0 & 0 \end{array} \right]\left[\begin{array}{cc} 13 & -5 \\ -5 & 2 \end{array} \right]\left[\begin{array}{ccc} 1 & 1 & 0 \\ 2 & 3 & 0 \end{array} \right] = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0\end{array} \right]\]
이 됩니다. 벡터 $\vec{b}$를 사영한 벡터는 $P \cdot \vec{b}$ 이므로 다음과 같습니다.
\[P \cdot \vec{b} = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0\end{array} \right]\left[\begin{array}{c} 4 \\ 5 \\ 6\end{array} \right] = \left[\begin{array}{c} 4 \\ 5 \\ 0\end{array} \right]\]
Normal Equation
사영 기법은 임의의 점들을 근사하는 함수를 찾는 데에 사용할 수 있습니다. 가장 간단하게 직선을 찾는 선형 회귀(Linear regression)의 예시부터 알아보겠습니다.

이미지 출처 : wikipedia - Linear_regression
위 그래프의 점을 각각 $(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$ 라고 하고 이를 근사하는 파란 직선을 $y = w_0 + w_1 x$ 라고 하겠습니다. 이 4개의 점을 모두 지나는 직선은 없으며 파란 직선은 직선과 점 사이의 거리를 최소화하는 조건을 만족하는 직선입니다.
각 점을 지나는 직선은 각각 $y_1 = w_0 + w_1 x_1, \quad y_2 = w_0 + w_1 x_2, \quad y_3 = w_0 + w_1 x_3, \quad y_4 = w_0 + w_1 x_4$ 조건을 만족하므로 식이 4개고 미지수가 2개인 연립방정식의 해를 구하는 것과 같습니다. 이를 행렬을 사용한 식으로 나타내면 아래와 같습니다.
\[\left[\begin{array}{cc} 1 & x_1 \\ 1 & x_2 \\ 1 & x_3 \\ 1 & x_4 \end{array} \right]\left[\begin{array}{c} w_0 \\ w_1 \end{array} \right] = \left[\begin{array}{c} y_0 \\ y_1 \\ y_2 \\ y_3 \end{array} \right]\]
위 식에서 $w_0, w_1$을 구하는 과정은 위에서 풀었던 $A\mathbf{x} = b$ 를 사영으로 푸는 방법과 동일합니다. 이렇게 사영 기법을 통해 회귀식의 미지수를 구하는 방법을 정규 방정식(Normal Equation) 또는 최소 제곱법(Least squares)이라고 합니다.
Projection
이번 시간에는 사영(Projection)에 대하여 알아보도록 하겠습니다. 위키백과에서는 사영의 뜻을 다음과 같이 서술하고 있습니다.
사영 또는 투영은 어떤 집합을 부분집합으로 특정한 조건을 만족시키면서 옮기는 작용이다.
즉, 벡터의 사영이란 특정 벡터를 다른 벡터 공간으로 옮기는 행위를 말합니다. 벡터의 사영에서 부분공간의 점들 중 거리가 가장 작은 곳으로 옮긴다는 특정 조건이 있습니다. 예를 들어, $\vec{a}$ 를 다른 벡터 $\vec{b}$ 위로 사영하고자 한다면 $\vec{a}$ 가 사영되는 지점인 $\vec{a^\prime}$ 과 원래 벡터 사이의 거리 $\vert\vec{a} - \vec{a^\prime}\vert$ 최소가 됩니다. 아래 그림은 벡터의 사영을 이미지로 나타낸 것입니다.

이미지 출처 : wikibooks.org
위 이미지에서 $\vec{v}$ 를 사영한 벡터는 둘 사이의 거리인 $\vert \vec{v} - \text{proj}_{[\vec{s}]}(\vec{p})\vert$를 최소화 하는 지점으로 결정됩니다.
Solve Equation
사영을 이용하면 또 다른 형태의 연립방정식의 해를 구할 수 있습니다. 식의 개수가 미지수의 개수보다 더 많은 경우입니다. 미지수의 개수가 2개이고 식이 3개인 경우를 평면상에 나타내면 아래와 같습니다. 물론, 운좋게 세 직선이 한 점에서 만날 수도 있으나 그런 경우는 제외하겠습니다.
이런 경우에는 정해진 하나의 해가 없습니다. 이 연립방정식을 행렬로 나타냈을 때의 $A$는 열의 개수보다 행의 개수가 많은 행렬이 됩니다. 이럴 때에는 해를 나타내는 벡터 $\vec{b}$ 가 $A$의 Column space 내부에 없기 때문에, $A$의 Column 스페이스와 거리가 최소가 되는 곳, 즉 $\vec{b}$ 를 $A$ 의 Column space로 사영한 곳을 해로 정하게 됩니다. 사영 벡터 $\vec{p} = \hat{c}\cdot A$ 라고 하면 $\vec{b} - \hat{c}\cdot A \perp \vec{a_i}$ 이므로 다음과 같은 식을 만족하게 됩니다.
\[\begin{aligned} \vec{a_1}^T (\vec{b} - &\hat{c}\cdot A) = 0 \\ \vec{a_2}^T (\vec{b} - &\hat{c}\cdot A) = 0 \\ &\vdots \\ \vec{a_n}^T (\vec{b} - &\hat{c}\cdot A) = 0 \\ \therefore A^T(\vec{b} - &\hat{c}\cdot A) = 0 \\ \end{aligned}\]식을 전개하여 $\hat{c}$에 대하여 정리하면
\[\hat{c}\cdot A^TA = A^T \cdot\vec{b} \\ \hat{c} = (A^TA)^{-1}A^T \cdot\vec{b}\]최종적으로 이 해를 구하기 위한 변환 행렬, 즉 사영 행렬(Projection matrix, $P$ )은 다음과 같이 나타낼 수 있습니다.
\[P = A(A^TA)^{-1}A^T \\ \because P\cdot \vec{b} = A \cdot \hat{c} = A(A^TA)^{-1}A^T \cdot\vec{b}\]$\vec{b}$ 벡터를 어떤 행렬 $A$의 Column space에 사영시키는 간단한 예시를 보겠습니다. 각 행렬과 벡터의 요소는 다음과 같습니다.
\[A = \left[\begin{array}{cc} 1 & 2 \\ 1 & 3 \\ 0 & 0 \end{array} \right] \\ \vec{b} = (4,5,6)^T\]$A$ 의 Column space는 $xy$ 평면이며, 이 공간으로의 사영시키는 행렬 $P$는 위 식을 사용하여 구할 수 있습니다.
\[A^TA = \left[\begin{array}{ccc} 1 & 1 & 0 \\ 2 & 3 & 0 \end{array} \right]\left[\begin{array}{cc} 1 & 2 \\ 1 & 3 \\ 0 & 0 \end{array} \right] = \left[\begin{array}{cc} 2 & 5 \\ 5 & 13 \end{array} \right] \\ \therefore (A^TA)^{-1} = \left[\begin{array}{cc} 13 & -5 \\ -5 & 2 \end{array} \right]\]사영 행렬 $P$ 를 구하는 식을 사용하면
\[P = A(A^TA)^{-1}A^T = \left[\begin{array}{cc} 1 & 2 \\ 1 & 3 \\ 0 & 0 \end{array} \right]\left[\begin{array}{cc} 13 & -5 \\ -5 & 2 \end{array} \right]\left[\begin{array}{ccc} 1 & 1 & 0 \\ 2 & 3 & 0 \end{array} \right] = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0\end{array} \right]\]이 됩니다. 벡터 $\vec{b}$를 사영한 벡터는 $P \cdot \vec{b}$ 이므로 다음과 같습니다.
\[P \cdot \vec{b} = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0\end{array} \right]\left[\begin{array}{c} 4 \\ 5 \\ 6\end{array} \right] = \left[\begin{array}{c} 4 \\ 5 \\ 0\end{array} \right]\]Normal Equation
사영 기법은 임의의 점들을 근사하는 함수를 찾는 데에 사용할 수 있습니다. 가장 간단하게 직선을 찾는 선형 회귀(Linear regression)의 예시부터 알아보겠습니다.

이미지 출처 : wikipedia - Linear_regression
위 그래프의 점을 각각 $(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$ 라고 하고 이를 근사하는 파란 직선을 $y = w_0 + w_1 x$ 라고 하겠습니다. 이 4개의 점을 모두 지나는 직선은 없으며 파란 직선은 직선과 점 사이의 거리를 최소화하는 조건을 만족하는 직선입니다.
각 점을 지나는 직선은 각각 $y_1 = w_0 + w_1 x_1, \quad y_2 = w_0 + w_1 x_2, \quad y_3 = w_0 + w_1 x_3, \quad y_4 = w_0 + w_1 x_4$ 조건을 만족하므로 식이 4개고 미지수가 2개인 연립방정식의 해를 구하는 것과 같습니다. 이를 행렬을 사용한 식으로 나타내면 아래와 같습니다.
\[\left[\begin{array}{cc} 1 & x_1 \\ 1 & x_2 \\ 1 & x_3 \\ 1 & x_4 \end{array} \right]\left[\begin{array}{c} w_0 \\ w_1 \end{array} \right] = \left[\begin{array}{c} y_0 \\ y_1 \\ y_2 \\ y_3 \end{array} \right]\]위 식에서 $w_0, w_1$을 구하는 과정은 위에서 풀었던 $A\mathbf{x} = b$ 를 사영으로 푸는 방법과 동일합니다. 이렇게 사영 기법을 통해 회귀식의 미지수를 구하는 방법을 정규 방정식(Normal Equation) 또는 최소 제곱법(Least squares)이라고 합니다.

Comments