배치 정규화 (Batch Normalization)
08 Feb 2021 | Deep-Learning
Batch Normalization
이번 게시물에서는 배치 정규화(Batch normalization)에 대해서 알아보겠습니다. 배치 정규화의 장점은 세 가지가 있습니다. 먼저 학습 속도를 빠르게 합니다. 학습률을 높게 설정해도 최적화가 잘 되기 때문이지요. 두 번째로 신경망을 가중치 초기화(Weight Initialization)나 하이퍼파라미터 설정에 대해 강건(Robust)하게 만들어줍니다. 즉, 이 값을 좀 더 자유롭게 설정해도 수렴이 잘 되지요. 마지막으로 오버피팅을 막아줍니다. 드롭아웃(Dropout)과 같은 스킬을 사용하지 않아도 모델이 일반화(Generalization)됩니다.
Normalization
신경망에 데이터를 넣을 때 입력값에 정규화를 해줍니다. 배치 정규화를 알아보기에 앞서 입력값을 정규화해주는 이유에 대해서 알아보겠습니다. 대부분의 데이터는 특성마다 가지는 값의 범위가 다릅니다.
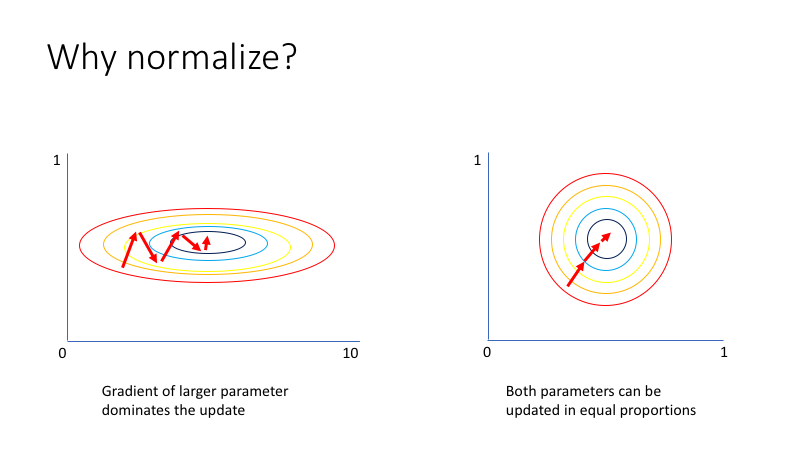
단순한 예로 성인의 손뼘 길이와 신장의 연관 관계를 알아보기 위한 데이터를 가지고 있다고 해보겠습니다. 신장를 특성으로 하는 데이터는 대략 $[145, 210]$ 범위를 가질 것입니다. 나머지 특성인 손뼘 길이는 $[15, 30]$ 정도의 범위를 가지겠지요. 위처럼 대부분의 데이터는 특성값에 따라 다른 범위를 가지는데요. 데이터의 분포를 그려보면 아래 그림의 왼쪽 그래프처럼 그려지게 됩니다.
이미지 출처 : www.jeremyjordan.me
문제는 왼쪽처럼 생긴 데이터는 비효율적인 최적화 경로를 갖는다는 점입니다. 주로 편차가 큰 특성의 파라미터를 갱신하는 방향으로 학습이 진행되기 때문이지요. 상대적으로 적은 편차를 갖는 특성의 영향력은 줄어듭니다. 위 그림에서도 X축 특성의 값을 최적화하는 방향으로만 학습이 진행되고, Y축에 나타나는 특성값은 상대적으로 무시되는 것을 볼 수 있습니다.
입력값 정규화는 이런 문제를 해결하기 위해서 사용하는 방법입니다. 정규화는 특성마다의 범위를 동일하게 만들어줍니다. 이와 같이 범위가 비슷해지면 학습 과정에서 모든 특성에 대한 파라미터가 동일하게 개선되어 훨씬 더 효율적인 최적화 경로를 갖게 되지요.
ICS(Internal Covariate Shift)
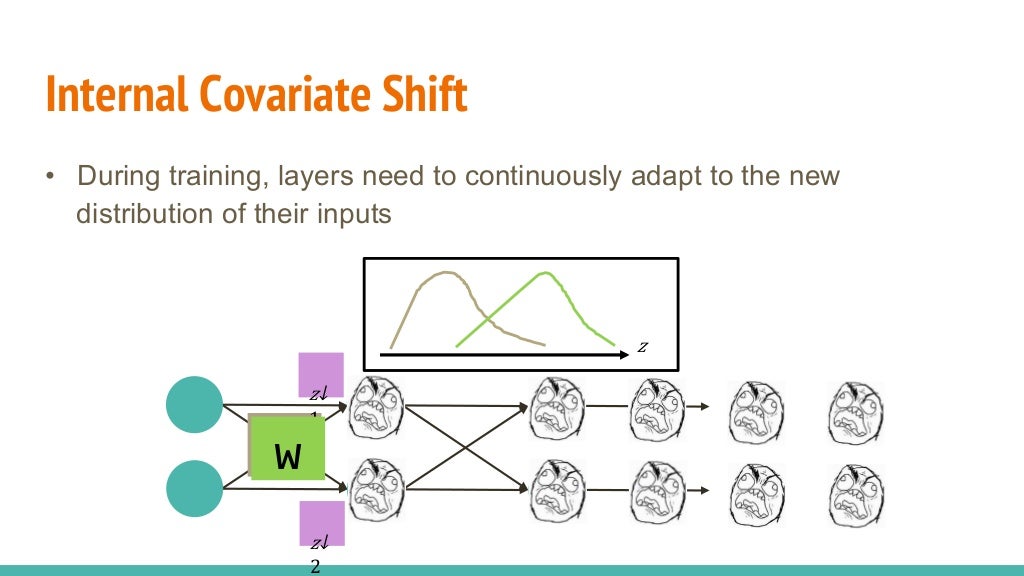
위와 같이 입력값은 신경망에 들어가기 전에 적당하게 조정해 줄 수 있습니다. 하지만 신경망 내부에서 파라미터와의 연산을 통해 은닉층을 빠져나오는 값은 다른 분포를 나타냅니다. 은닉층마다 이런 현상이 생긴다면 학습이 제대로 이루어지지 않지요.

이미지 출처 : imgur.com
이렇게 신경망 내부의 은닉층마다 입력되는 값의 분포가 달라지는 현상을 ICS(Internal covariate shift, 내부 공변량 변화)라고 합니다.
이미지 출처 : www.slideshare.net/ssuser950871
배치 정규화는 “ICS를 해결해주면 신경망의 성능이 훨씬 더 좋아지지 않을까?”라는 아이디어에서 시작되었습니다.
Batch Normalization
배치 정규화는 완전 연결층(Fully Connected Layer)과 활성화 함수 사이에 배치 정규화 층(Batch norm layer)을 하나 더 삽입합니다. 층이 추가된 후의 순서는 아래 이미지와 같습니다.

이미지 출처 : stats.stackexchange.com
배치 정규화 층에서는 완전 연결 층에서 계산된 값을 미니배치 단위로 정규화 합니다. 미니배치 $B$ 의 사이즈가 $m$ 이라면 각 데이터의 평균 $\mu_B$ 와 분산 $\sigma_B^2$ 를 구하고 표준화(Standardization)을 수행하여 $\hat{x_i}$ 를 구합니다.
\[\begin{aligned}
\mu_B &\leftarrow \frac{1}{m} \sum_{i=1}^m x_i \\
\sigma_B^2 &\leftarrow \frac{1}{m} (x_i - \mu_B)^2 \\
\hat{x_i} &\leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2+\epsilon}}
\end{aligned}\]
위 식에서 $\epsilon$ 은 계산 안정성을 위한 매우 작은 상수입니다. 이렇게 계산된 값은 표준정규분포 $N(0,1)$ 를 나타냅니다. 하지만 여기서 끝나면 안됩니다. 표준정규분포에서는 $68.26\%$ 만큼이 $[-1,1]$ 범위에 있고, $95.44\%$ 의 값이 $[-2,2]$ 범위에 있습니다. 하지만 이 구간에서는 활성화 함수인 시그모이드 함수가 선형 함수에 근사한 형태를 가집니다.

로지스틱 함수(Logistic function)와 y=0.24x + 0.5

하이퍼탄젠트 함수(Hypertangent function)와 y=0.9x
이곳에서 알아본 것처럼 활성화 함수로 선형 함수를 사용하게 되면 층을 깊게 쌓을 때의 이점이 사라집니다. 이런 문제를 해결하기 위해서 정규화한 값 $\hat{x_i}$ 을 적당이 조작해줍니다. 파라미터 $\gamma, \beta$ 를 각각 곱해주고 더해준 값 $y_i$ 를 활성화 함수에 입력하지요. 수식으로 나타낸 배치 정규화 층의 최종 출력값은 다음과 같습니다.
\[y_i \leftarrow \gamma_j\hat{x_i} + \beta_j\]
이 때 곱해지고 더해지는 파라미터 $\gamma, \beta$ 는 각 노드마다 다른 값이 적용됩니다. 특정 층의 노드가 64개라면 배치 정규화 층에도 파라미터가 각각 크만큼 있는 것이지요. $\gamma_j, \beta_j (j = 1, \cdots, 64)$ 가 됩니다. 이 때 $y$ 의 분포는 $N(\beta_j, \gamma_j^2)$ 이며 $\gamma_i, \beta_i$ 는 학습을 통해 결정됩니다. 배치 정규화의 계산 그래프는 아래와 같습니다.

이미지 출처 : costapt.github.io
배치 정규화를 사용했을 때와 사용하지 않았을 때 학습 데이터셋과 검증 데이터셋에 대한 학습 결과는 아래와 같습니다.

이미지 출처 : learnopencv.com
배치 정규화를 했을 때 훨씬 더 좋은 결과를 보여주는 것을 볼 수 있습니다.
However,
배치 정규화의 효과에 대해서는 의심할 바가 없습니다. 많은 모델이 배치 정규화를 통해서 좋은 성능을 보여왔습니다. 그런데 배치 정규화가 이렇게 좋은 성능을 보이는 이유가 정말 ICS를 해결해서일까요? 아니, 배치 정규화가 진짜로 ICS를 해결해주기는 하는 것일까요?
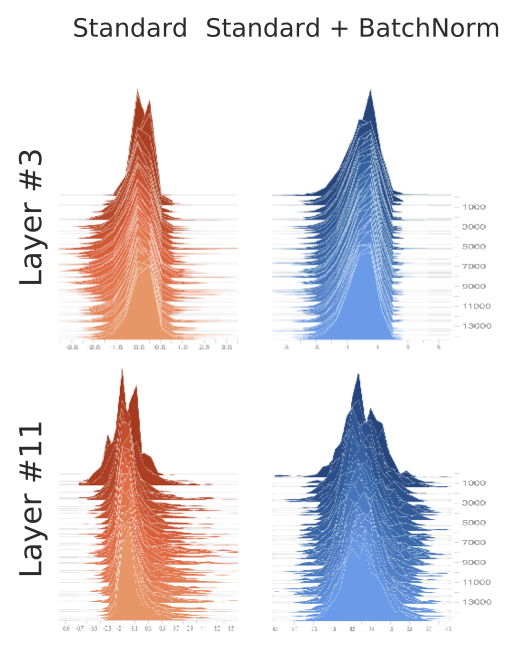
2018년에는 배치 정규화가 어떻게 최적화에 도움을 주는지에 대해 연구한 논문이 발표되었습니다. 논문에 따르면 배치 정규화가 ICS를 해결해주지도 못한다는 것이지요. 아래는 배치 정규화를 적용했을 때(오른쪽)와 적용하지 않았을 때(왼쪽), 3번째 층과 11번째 층에 들어오는 값의 분포를 시각화한 것입니다. 학습에 사용되는 미니배치마다 그래프를 그렸습니다.
이미지 출처 : gradientscience.org
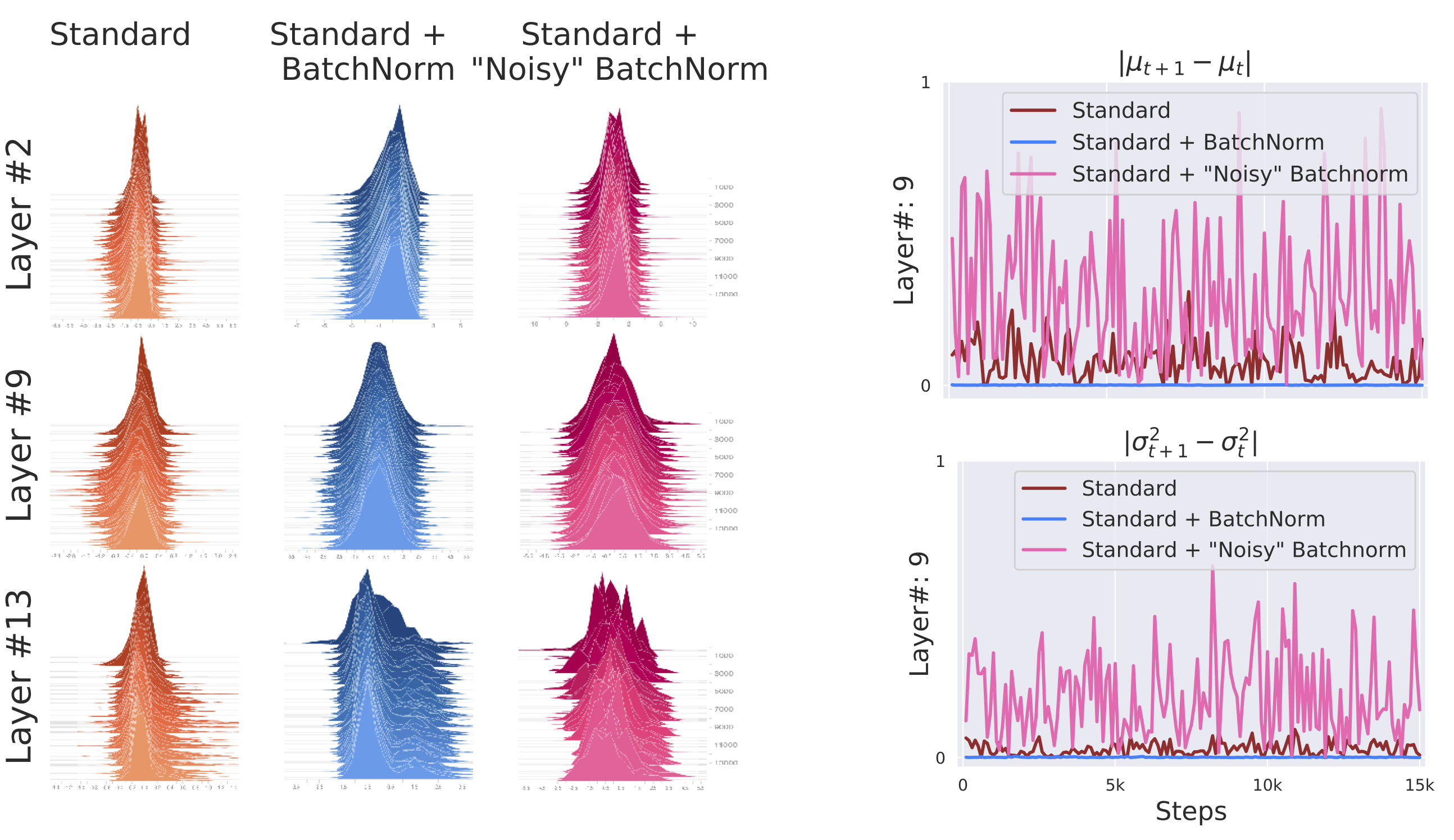
그림을 보면 둘 사이에 획기적인 변화가 없습니다. 3번째 층이든 11번째 층이든 배치 정규화를 사용했을 때와 그렇지 않았을 때 큰 차이가 없음을 볼 수 있지요. 논문 저자들은 배치 정규화를 적용한 뒤에 노이즈를 주어 일부러 분포를 흐트린 모델을 추가하여 실험해보기도 했습니다. 아래는 세 모델을 시각화한 결과입니다.
이미지 출처 : gradientscience.org
노이즈가 추가된 모델은 반복 스텝마다 매우 다른 분포를 보이고 있습니다. 그렇다면 세 모델의 성능은 각각 어떻게 될까요? 세 모델의 성능을 비교한 학습 그래프입니다.
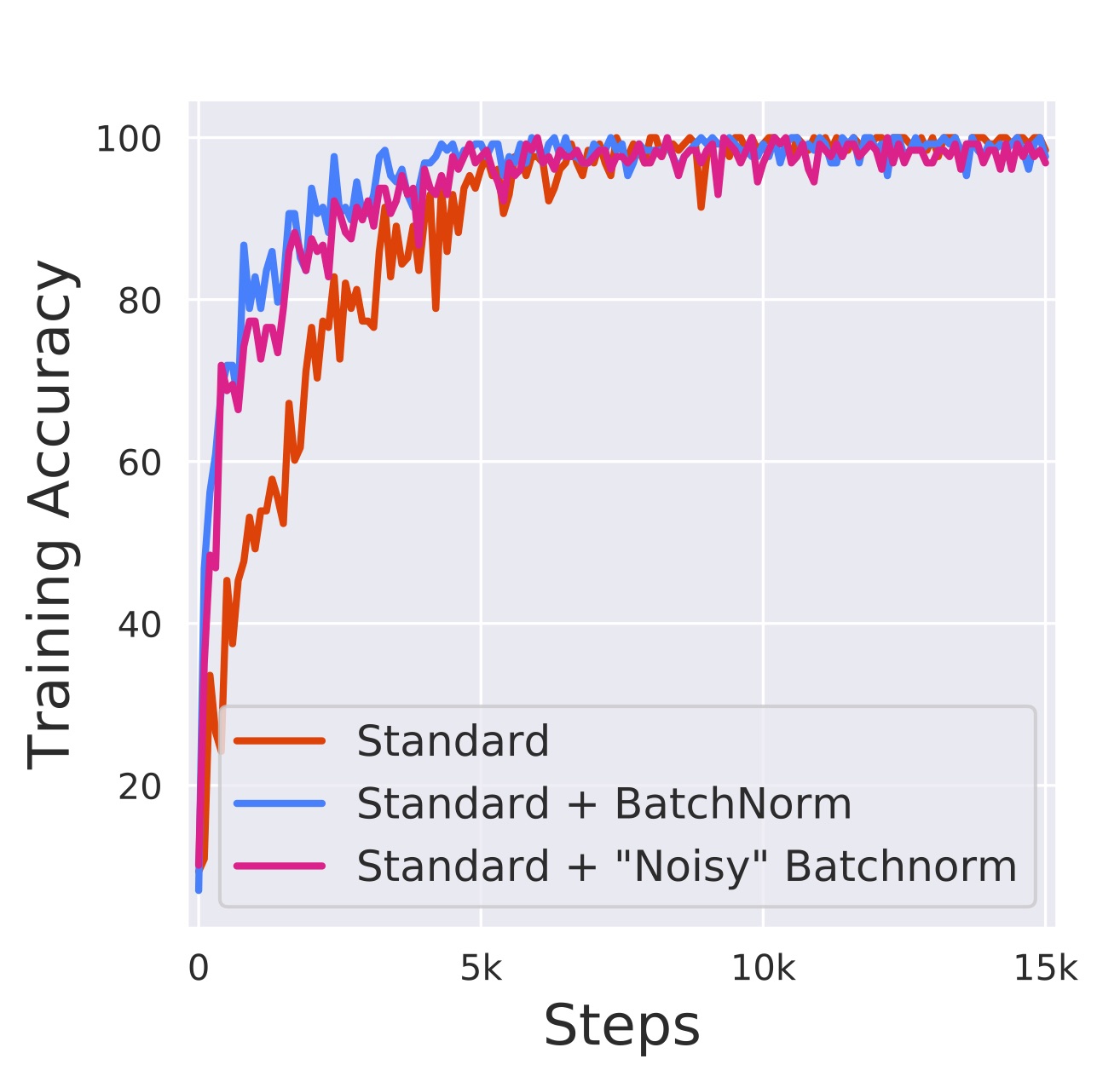
이미지 출처 : gradientscience.org
노이즈가 추가된 모델은 ICS가 오히려 심해졌음에도 배치 정규화를 적용하지 않은 모델보다 훨씬 더 좋은 성능을 보였습니다. 논문을 통해 배치 정규화가 ICS를 해결하는지도 알 수 없고, ICS를 해결하는 것이 좋은 성능을 보장하는 것도 아님을 증명했습니다. 그렇다면 배치 정규화는 실질적으로 어떤 작용을하여 최적화에 어떤 도움을 가져다주는 것일까요?
Smoothing!
논문의 저자는 배치 정규화가 스무딩(Smoothing)을 만들어준다고 이야기하고 있습니다. 배치 정규화를 적용하지 않은 손실 함수가 왼쪽과 같이 생겼다면, 배치 정규화를 적용한 손실 함수는 오른쪽처럼 생겼다는 것이지요.

이미지 출처 : Visualizing the Loss Landscape of Neural Nets
본 실험에서 손실 함수의 평면과 기울기를 나타낸 그래프입니다. 배치 정규화를 적용했을 때가 그렇지 않을 때보다 훨씬 더 완만한 경사를 가지는 것을 볼 수 있습니다.
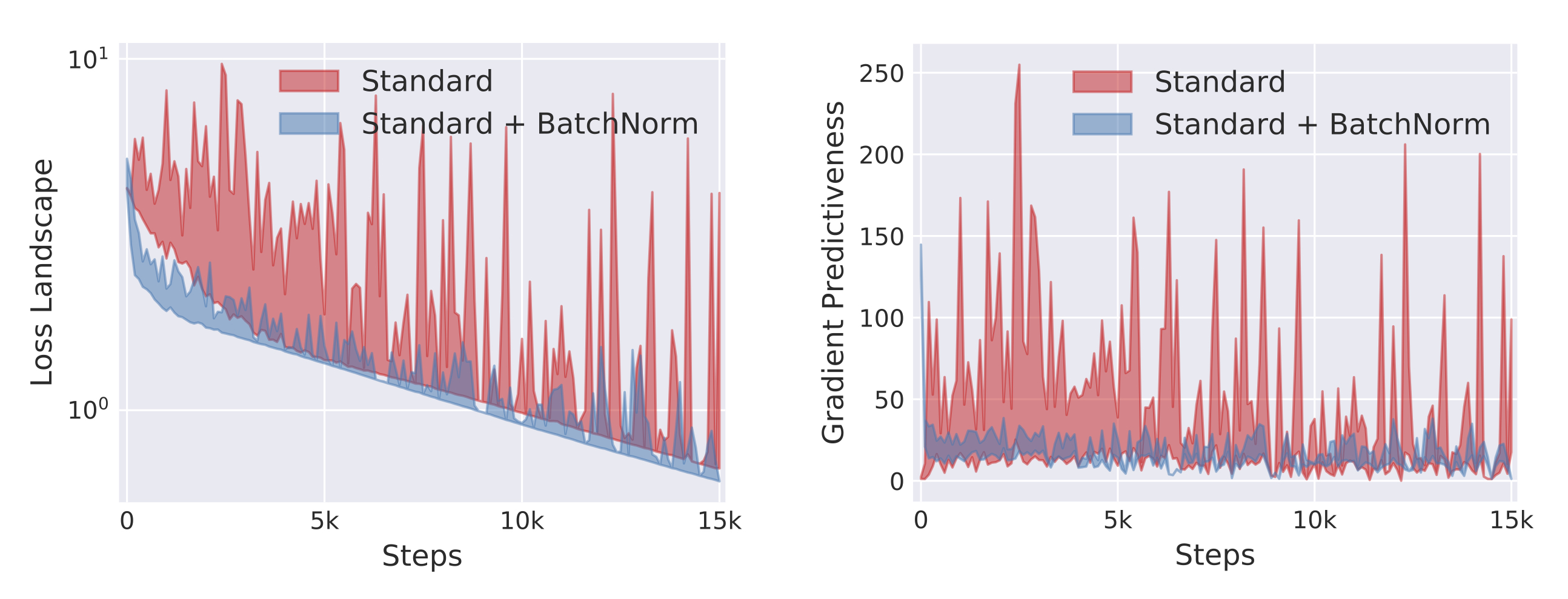
이미지 출처 : gradientscience.org
결론은 배치 정규화가 좋은 성능을 보이는 이유가 ICS를 해결했기 때문이 아니라 스무딩 덕분이라는 것이지요. 마지막으로 배치 정규화의 장점을 다시 떠올려 보겠습니다. 첫 번째는 “학습률을 크게 설정할 수 있다.”, 두 번째는 “가중치 초기화에 덜 민감하다.”, 세 번째는 “모델이 잘 일반화되어 있다.”는 것이었습니다. 배치 정규화가 스무딩, 즉 복잡한 손실 함수의 평면을 부드럽게 만들어준다는 것을 알고 있다면 위와 같은 장점이 생김을 자연스레 이해할 수 있습니다. 배치 정규화는 여러 모델에 대해서 간단한 아이디어에도 좋은 성능을 보여주기 때문에 SOTA를 달성한 많은 모델에 쓰였던 기법입니다.
Batch Normalization
이번 게시물에서는 배치 정규화(Batch normalization)에 대해서 알아보겠습니다. 배치 정규화의 장점은 세 가지가 있습니다. 먼저 학습 속도를 빠르게 합니다. 학습률을 높게 설정해도 최적화가 잘 되기 때문이지요. 두 번째로 신경망을 가중치 초기화(Weight Initialization)나 하이퍼파라미터 설정에 대해 강건(Robust)하게 만들어줍니다. 즉, 이 값을 좀 더 자유롭게 설정해도 수렴이 잘 되지요. 마지막으로 오버피팅을 막아줍니다. 드롭아웃(Dropout)과 같은 스킬을 사용하지 않아도 모델이 일반화(Generalization)됩니다.
Normalization
신경망에 데이터를 넣을 때 입력값에 정규화를 해줍니다. 배치 정규화를 알아보기에 앞서 입력값을 정규화해주는 이유에 대해서 알아보겠습니다. 대부분의 데이터는 특성마다 가지는 값의 범위가 다릅니다.
단순한 예로 성인의 손뼘 길이와 신장의 연관 관계를 알아보기 위한 데이터를 가지고 있다고 해보겠습니다. 신장를 특성으로 하는 데이터는 대략 $[145, 210]$ 범위를 가질 것입니다. 나머지 특성인 손뼘 길이는 $[15, 30]$ 정도의 범위를 가지겠지요. 위처럼 대부분의 데이터는 특성값에 따라 다른 범위를 가지는데요. 데이터의 분포를 그려보면 아래 그림의 왼쪽 그래프처럼 그려지게 됩니다.

이미지 출처 : www.jeremyjordan.me
문제는 왼쪽처럼 생긴 데이터는 비효율적인 최적화 경로를 갖는다는 점입니다. 주로 편차가 큰 특성의 파라미터를 갱신하는 방향으로 학습이 진행되기 때문이지요. 상대적으로 적은 편차를 갖는 특성의 영향력은 줄어듭니다. 위 그림에서도 X축 특성의 값을 최적화하는 방향으로만 학습이 진행되고, Y축에 나타나는 특성값은 상대적으로 무시되는 것을 볼 수 있습니다.
입력값 정규화는 이런 문제를 해결하기 위해서 사용하는 방법입니다. 정규화는 특성마다의 범위를 동일하게 만들어줍니다. 이와 같이 범위가 비슷해지면 학습 과정에서 모든 특성에 대한 파라미터가 동일하게 개선되어 훨씬 더 효율적인 최적화 경로를 갖게 되지요.
ICS(Internal Covariate Shift)
위와 같이 입력값은 신경망에 들어가기 전에 적당하게 조정해 줄 수 있습니다. 하지만 신경망 내부에서 파라미터와의 연산을 통해 은닉층을 빠져나오는 값은 다른 분포를 나타냅니다. 은닉층마다 이런 현상이 생긴다면 학습이 제대로 이루어지지 않지요.

이미지 출처 : imgur.com
이렇게 신경망 내부의 은닉층마다 입력되는 값의 분포가 달라지는 현상을 ICS(Internal covariate shift, 내부 공변량 변화)라고 합니다.

이미지 출처 : www.slideshare.net/ssuser950871
배치 정규화는 “ICS를 해결해주면 신경망의 성능이 훨씬 더 좋아지지 않을까?”라는 아이디어에서 시작되었습니다.
Batch Normalization
배치 정규화는 완전 연결층(Fully Connected Layer)과 활성화 함수 사이에 배치 정규화 층(Batch norm layer)을 하나 더 삽입합니다. 층이 추가된 후의 순서는 아래 이미지와 같습니다.

이미지 출처 : stats.stackexchange.com
배치 정규화 층에서는 완전 연결 층에서 계산된 값을 미니배치 단위로 정규화 합니다. 미니배치 $B$ 의 사이즈가 $m$ 이라면 각 데이터의 평균 $\mu_B$ 와 분산 $\sigma_B^2$ 를 구하고 표준화(Standardization)을 수행하여 $\hat{x_i}$ 를 구합니다.
\[\begin{aligned} \mu_B &\leftarrow \frac{1}{m} \sum_{i=1}^m x_i \\ \sigma_B^2 &\leftarrow \frac{1}{m} (x_i - \mu_B)^2 \\ \hat{x_i} &\leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2+\epsilon}} \end{aligned}\]위 식에서 $\epsilon$ 은 계산 안정성을 위한 매우 작은 상수입니다. 이렇게 계산된 값은 표준정규분포 $N(0,1)$ 를 나타냅니다. 하지만 여기서 끝나면 안됩니다. 표준정규분포에서는 $68.26\%$ 만큼이 $[-1,1]$ 범위에 있고, $95.44\%$ 의 값이 $[-2,2]$ 범위에 있습니다. 하지만 이 구간에서는 활성화 함수인 시그모이드 함수가 선형 함수에 근사한 형태를 가집니다.
로지스틱 함수(Logistic function)와 y=0.24x + 0.5
하이퍼탄젠트 함수(Hypertangent function)와 y=0.9x
이곳에서 알아본 것처럼 활성화 함수로 선형 함수를 사용하게 되면 층을 깊게 쌓을 때의 이점이 사라집니다. 이런 문제를 해결하기 위해서 정규화한 값 $\hat{x_i}$ 을 적당이 조작해줍니다. 파라미터 $\gamma, \beta$ 를 각각 곱해주고 더해준 값 $y_i$ 를 활성화 함수에 입력하지요. 수식으로 나타낸 배치 정규화 층의 최종 출력값은 다음과 같습니다.
\[y_i \leftarrow \gamma_j\hat{x_i} + \beta_j\]이 때 곱해지고 더해지는 파라미터 $\gamma, \beta$ 는 각 노드마다 다른 값이 적용됩니다. 특정 층의 노드가 64개라면 배치 정규화 층에도 파라미터가 각각 크만큼 있는 것이지요. $\gamma_j, \beta_j (j = 1, \cdots, 64)$ 가 됩니다. 이 때 $y$ 의 분포는 $N(\beta_j, \gamma_j^2)$ 이며 $\gamma_i, \beta_i$ 는 학습을 통해 결정됩니다. 배치 정규화의 계산 그래프는 아래와 같습니다.

이미지 출처 : costapt.github.io
배치 정규화를 사용했을 때와 사용하지 않았을 때 학습 데이터셋과 검증 데이터셋에 대한 학습 결과는 아래와 같습니다.

이미지 출처 : learnopencv.com
배치 정규화를 했을 때 훨씬 더 좋은 결과를 보여주는 것을 볼 수 있습니다.
However,
배치 정규화의 효과에 대해서는 의심할 바가 없습니다. 많은 모델이 배치 정규화를 통해서 좋은 성능을 보여왔습니다. 그런데 배치 정규화가 이렇게 좋은 성능을 보이는 이유가 정말 ICS를 해결해서일까요? 아니, 배치 정규화가 진짜로 ICS를 해결해주기는 하는 것일까요?
2018년에는 배치 정규화가 어떻게 최적화에 도움을 주는지에 대해 연구한 논문이 발표되었습니다. 논문에 따르면 배치 정규화가 ICS를 해결해주지도 못한다는 것이지요. 아래는 배치 정규화를 적용했을 때(오른쪽)와 적용하지 않았을 때(왼쪽), 3번째 층과 11번째 층에 들어오는 값의 분포를 시각화한 것입니다. 학습에 사용되는 미니배치마다 그래프를 그렸습니다.

이미지 출처 : gradientscience.org
그림을 보면 둘 사이에 획기적인 변화가 없습니다. 3번째 층이든 11번째 층이든 배치 정규화를 사용했을 때와 그렇지 않았을 때 큰 차이가 없음을 볼 수 있지요. 논문 저자들은 배치 정규화를 적용한 뒤에 노이즈를 주어 일부러 분포를 흐트린 모델을 추가하여 실험해보기도 했습니다. 아래는 세 모델을 시각화한 결과입니다.

이미지 출처 : gradientscience.org
노이즈가 추가된 모델은 반복 스텝마다 매우 다른 분포를 보이고 있습니다. 그렇다면 세 모델의 성능은 각각 어떻게 될까요? 세 모델의 성능을 비교한 학습 그래프입니다.

이미지 출처 : gradientscience.org
노이즈가 추가된 모델은 ICS가 오히려 심해졌음에도 배치 정규화를 적용하지 않은 모델보다 훨씬 더 좋은 성능을 보였습니다. 논문을 통해 배치 정규화가 ICS를 해결하는지도 알 수 없고, ICS를 해결하는 것이 좋은 성능을 보장하는 것도 아님을 증명했습니다. 그렇다면 배치 정규화는 실질적으로 어떤 작용을하여 최적화에 어떤 도움을 가져다주는 것일까요?
Smoothing!
논문의 저자는 배치 정규화가 스무딩(Smoothing)을 만들어준다고 이야기하고 있습니다. 배치 정규화를 적용하지 않은 손실 함수가 왼쪽과 같이 생겼다면, 배치 정규화를 적용한 손실 함수는 오른쪽처럼 생겼다는 것이지요.
이미지 출처 : Visualizing the Loss Landscape of Neural Nets
본 실험에서 손실 함수의 평면과 기울기를 나타낸 그래프입니다. 배치 정규화를 적용했을 때가 그렇지 않을 때보다 훨씬 더 완만한 경사를 가지는 것을 볼 수 있습니다.

이미지 출처 : gradientscience.org
결론은 배치 정규화가 좋은 성능을 보이는 이유가 ICS를 해결했기 때문이 아니라 스무딩 덕분이라는 것이지요. 마지막으로 배치 정규화의 장점을 다시 떠올려 보겠습니다. 첫 번째는 “학습률을 크게 설정할 수 있다.”, 두 번째는 “가중치 초기화에 덜 민감하다.”, 세 번째는 “모델이 잘 일반화되어 있다.”는 것이었습니다. 배치 정규화가 스무딩, 즉 복잡한 손실 함수의 평면을 부드럽게 만들어준다는 것을 알고 있다면 위와 같은 장점이 생김을 자연스레 이해할 수 있습니다. 배치 정규화는 여러 모델에 대해서 간단한 아이디어에도 좋은 성능을 보여주기 때문에 SOTA를 달성한 많은 모델에 쓰였던 기법입니다.

Comments