해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

Wrapper

래퍼(Wrapper)는 특성 선택(Feature selection)에 속하는 방법 중 하나로, 반복되는 알고리즘을 사용하는 지도 학습 기반의 차원 축소법입니다. 래퍼 방식에는 전진 선택(Forward selection), 후진 제거(Backward elimination), Stepwise selection 방식 뿐만아니라 유전 알고리즘(Genetic algorithm) 방식도 사용됩니다. 이번 게시물에서는 각 방법들에 대해 자세히 알아보겠습니다.

Exhaustive Search

완전 탐색(Exhaustive search)은 모든 특성 선택 방법 중 가장 단순한 방식입니다. 예를 들어, 특성이 3개 $x_1,x_2,x_3$인 데이터가 있다고 해보겠습니다. 이 때 완전 탐색 방법을 사용하면 다음의 특성 조합에 대해 모델을 모두 실험해보고 가장 성능이 좋은 것을 고릅니다.

[f(x_1),f(x_2),f(x_3),f(x_1,x_2),f(x_1,x_3),f(x_2,x_3),f(x_1,x_2,x_3)]

완전 탐색 방식의 가장 좋은 점은 언제나 Global optimum(전역 최적점)을 찾을 수 있다는 점입니다. 순서에 상관없이 모든 특성 조합에 대하여 모델을 시험해 보기 때문에 Local optimum(지역 최적점)에 빠질 우려가 없습니다.

하지만 완전 탐색을 사용하면 데이터셋의 특성이 $n$개 일 때, $2^n-1$ 만큼의 모델을 평가해야 합니다. 위의 예에서도 3개의 특성을 기준으로 완전 탐색을 사용하였더니 $2^3-1 = 7$개의 모델을 평가하였습니다. 특성의 개수에 대하여 지수적으로 증가하므로 특성의 개수가 늘어나면 모델 평가 횟수가 엄청나게 많아지게 됩니다. $n=30$ 이라면 $2^{30}-1$ 회, 즉 10억 번 이상의 모델 평가를 수행해야 합니다. 이런 이유에서 완전 탐색 방식은 현실적으로 사용 불가능합니다.

앞으로 알아볼 다른 알고리즘과 비교하기 위해서 시간-성능 그래프에 완전 탐색을 나타내어 보겠습니다. 완전 탐색은 최고의 성능을 보여주지만 최고 오랜 시간을 필요로하기 때문에 아래와 같이 나타낼 수 있습니다.

Forward Selection / Backward Elimination

다음으로 전진 선택과 후진 제거를 알아보겠습니다. 이 두 방법은 성능을 어느 정도 유지하면서 전역 탐색에서 걸리는 시간을 극적으로 줄인 방법입니다. 시간-성능 그래프에 두 방법을 나타내면 다음과 같이 나타낼 수 있습니다.

Forward Selection

전진 선택(Forward selection)은 가장 유의미한 특성을 선택해나가는 방식 입니다. 아무런 특성이 없는 상태부터 시작해서 특성을 늘려나가는 방향(Forward)으로 나아갑니다. 매 단계마다 가장 성능이 좋은 특성을 선택한 뒤에 유의미한 성능이 없을 때까지 이 과정을 실행해 나갑니다. 아래는 전진 선택의 과정을 나타낸 이미지입니다.

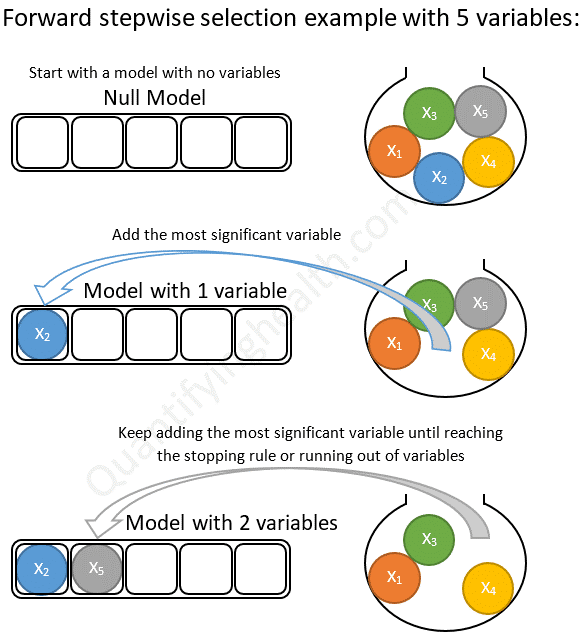
이미지 출처 : quantifyinghealth.com

특성이 5개 $x_1,x_2,x_3,x_4,x_5$인 데이터셋에 전진 선택 방식을 적용하여 특성 선택을 해보겠습니다(위 그림과는 관련이 없습니다). 먼저 1개의 특성만 가지는 모델의 성능을 비교합니다. 비교 성능으로는 조정된 결정계수(adjusted R-squared, $R^2_\text{adj}$)를 사용하겠습니다.

[\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 \qquad R^2\text{adj} = 0.32\ \hat{y} = \hat{\beta_0} + \hat{\beta_2}x_2 \qquad R^2\text{adj} = 0.45
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 \qquad R^2\text{adj} = 0.53
\hat{y} = \hat{\beta_0} + \hat{\beta_4}x_4 \qquad R^2\text{adj} = 0.35
\hat{y} = \hat{\beta_0} + \hat{\beta_5}x_5 \qquad R^2_\text{adj} = 0.46]

$x_3$을 선택했을 때의 성능이 가장 좋으므로 이 특성을 고정한 뒤에 $\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3$ 을 대조군으로 놓고 동일한 과정을 반복합니다.

[\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_1}x_1 \qquad R^2\text{adj} = 0.55
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_2}x_2 \qquad R^2\text{adj} = 0.58
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 \qquad R^2\text{adj} = 0.71
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.66]

$x_4$의 특성을 추가적으로 선택했을 때의 성능이 가장 좋으므로 $\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4$ 를 대조군으로 놓고 동일한 과정을 반복합니다.

[\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_1}x_1 \qquad R^2\text{adj} = 0.71
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_2}x_2 \qquad R^2\text{adj} = 0.70
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_3}x_5 \qquad R^2_\text{adj} = 0.69]

$x_1,x_2,x_5$중에서 어떤 특성을 추가하더라도 대조군인 $\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4$ 보다 성능이 좋아지지 않았으므로 여기서 과정을 멈추고 $\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4$ 을 특성 선택의 결과물로 선정합니다.

Backward Elimination

후진 제거(Backward elimination)는 무의미한 특성을 제거해나가는 방식 입니다. 반대로 모든 특성을 가진 모델에서 시작하여 특성을 하나씩 줄여나가는 방향(Backward)으로 나아갑니다. 특성을 제거했을 때 가장 성능이 좋은 모델을 선택함며 유의미한 성능 저하가 나타날 때까지 이 과정을 반복합니다. 아래는 후진 제거의 과정을 나타낸 이미지입니다.

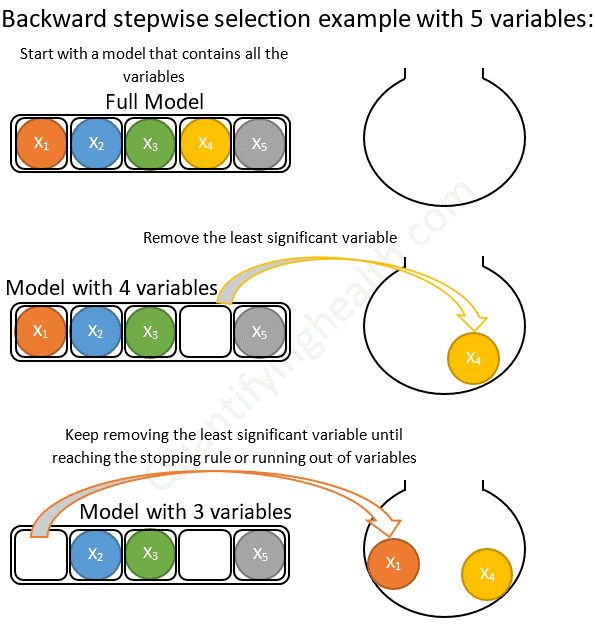
이미지 출처 : quantifyinghealth.com

동일하게 5개의 특성을 가진 데이터셋에 후진 제거를 사용하여 특성 선택을 해보겠습니다(위 그림과는 관련이 없습니다). 아래 예시에서 유의미한 성능저하를 결정하는 $R^2_\text{adj}$의 임계값은 $0.03$으로 하겠습니다. 먼저 모든 특성을 사용한 모델을 대조군으로 놓겠습니다.

[\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 + \hat{\beta_2}x_2 + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_5}x_5 \qquad R^2_\text{adj} = 0.73]

이제 특성을 하나씩 제거한 뒤에 성능을 비교합니다.

[\hat{y} = \hat{\beta_0} + \quad \qquad \hat{\beta_2}x_2 + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.73
\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 + \quad \qquad \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.71
\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 + \hat{\beta_2}x_2 + \quad \qquad \hat{\beta_4}x_4 + \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.64
\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 + \hat{\beta_2}x_2 + \hat{\beta_3}x_3 + \quad \qquad \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.69
\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 + \hat{\beta_2}x_2 + \hat{\beta_3}x_3 + \hat{\beta_4}x_4\quad \qquad \qquad R^2_\text{adj} = 0.66\]

$x_1$특성을 제거한 모델이 가장 높은 성능을 보였으며 $R^2_\text{adj}$이 임계값보다 적은 성능저하를 보였으므로 이 모델을 대조군으로 사용한 뒤에 동일한 과정을 반복합니다.

[\hat{y} = \hat{\beta_0} + \quad \qquad \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.69
\hat{y} = \hat{\beta_0} + \hat{\beta_2}x_2 + \quad \qquad \hat{\beta_4}x_4 + \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.67
\hat{y} = \hat{\beta_0} + \hat{\beta_2}x_2 + \hat{\beta_3}x_3 + \quad \qquad \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.71
\hat{y} = \hat{\beta_0} + \hat{\beta_2}x_2 + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 \quad \qquad \qquad R^2\text{adj} = 0.70]

$x_4$특성을 제거한 모델이 가장 높은 성능을 보였으며 $R^2_\text{adj}$이 임계값보다 적은 성능저하를 보였으므로 이 모델을 대조군으로 사용한 뒤에 동일한 과정을 반복합니다.

[\hat{y} = \hat{\beta_0} + \quad \qquad \hat{\beta_3}x_3 + \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.66
\hat{y} = \hat{\beta_0} + \hat{\beta_2}x_2 + \quad \qquad \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.54
\hat{y} = \hat{\beta_0} + \hat{\beta_2}x_2 + \hat{\beta_3}x_3 \quad \qquad \qquad R^2_\text{adj} = 0.56]

$x_4$특성을 제거한 모델이 가장 높은 성능을 보였지만, 이 모델의 $R^2_\text{adj}$은 대조군에 비하여 임곗값보다 더 많이 감소한 것을 볼 수 있습니다. 그렇기 때문에 대조군에 해당하는 $\hat{y} = \hat{\beta_0} + \hat{\beta_2}x_2 + \hat{\beta_3}x_3 + \hat{\beta_5}x_5$을 최종 모델로 선택합니다.

Stepwise Selection

전진 선택에서는 한 번 선택된 특성은 제거되지 않고, 후진 제거에서는 한 번 제거된 특성은 다시 선택되지 않습니다. 그렇기 때문에 두 방법 모두 더 많은 특성 조합에 대해 모델을 평가할 수 없다는 단점을 가지고 있습니다. Stepwise selection은 전진 선택과 후진 제거 방식을 매 단계마다 반복하여 적용하는 방식입니다. 이전 두 방법보다는 더 오래 걸리지만 최적의 변수 조합을 찾을 확률이 높습니다. Stepwise selection을 시간-성능 그래프에 표시하면 아래와 같이 나타나게 됩니다.

전진 선택과 후진 제거를 단계별로(Stepwise) 반복하여 적용할 뿐 특별히 다른 방식을 적용하지는 않습니다. 5개의 특성을 가지고 있는 데이터셋에 Stepwise selection을 적용하여 특성 선택을 진행해보겠습니다. 먼저 전진 선택을 적용합니다.

[\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 \qquad R^2\text{adj} = 0.32\ \hat{y} = \hat{\beta_0} + \hat{\beta_2}x_2 \qquad R^2\text{adj} = 0.45
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 \qquad R^2\text{adj} = 0.53
\hat{y} = \hat{\beta_0} + \hat{\beta_4}x_4 \qquad R^2\text{adj} = 0.35
\hat{y} = \hat{\beta_0} + \hat{\beta_5}x_5 \qquad R^2_\text{adj} = 0.46]

가장 성능이 좋은 모델을 선택합니다. 이어 선택된 모델 $\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3$에 후진 제거를 적용하면 제거할 특성이 하나뿐이므로 제대로 적용되지 않습니다. 다시 전진 선택을 수행하겠습니다.

[\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_1}x_1 \qquad R^2\text{adj} = 0.55
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_2}x_2 \qquad R^2\text{adj} = 0.58
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 \qquad R^2\text{adj} = 0.71
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_5}x_5 \qquad R^2\text{adj} = 0.66]

성능이 가장 좋은 모델은 $\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4$ 입니다. 이 모델에 후진 제거를 수행하면 어차피 $\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3$이 선택될 것이므로 제대로 적용되지는 않습니다. 다시 전진 선택을 수행하겠습니다. (예시를 위해서 전진 선택에서의 예시와 다른 $R^2_\text{adj}$값을 사용하겠습니다)

[\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_1}x_1 \qquad R^2\text{adj} = 0.75
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_2}x_2 \qquad R^2\text{adj} = 0.70
\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_3}x_5 \qquad R^2_\text{adj} = 0.69]

성능이 가장 좋은 모델은 $\hat{y} = \hat{\beta_0} + \hat{\beta_3}x_3 + \hat{\beta_4}x_4 + \hat{\beta_1}x_1$ 입니다. 이 단계부터는 후진 제거가 제대로 작동하게 됩니다. 이 모델을 대조군으로 두고 후진 제거를 수행해보겠습니다. 전진 선택과 후진 제거의 종료 기준이 되는 임계값은 여전히 위와 같은 $0.03$으로 하겠습니다.

[\hat{y} = \hat{\beta_0} + \quad \qquad \hat{\beta_3}x_3 + \hat{\beta_4}x_4 \qquad R^2\text{adj} = 0.70
\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 + \quad \qquad \hat{\beta_4}x_4 \qquad R^2\text{adj} = 0.54
\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 + \hat{\beta_3}x_3 \quad \qquad \qquad R^2_\text{adj} = 0.73]

최고 성능을 보이는 $\hat{y} = \hat{\beta_0} + \hat{\beta_1}x_1 + \hat{\beta_3}x_3$모델의 성능은 후진 제거 임계값보다 더 적게 감소되었으므로 반복을 멈추지 않고 다시 전진 선택을 수행하면 됩니다. 이렇게 전진 선택과 후진 제거를 한 번씩 적용하여도 특성의 변화가 없을 때까지 알고리즘을 반복하면 됩니다. 이 방법은 전진 선택이나 후진 제거가 가지고 있던 “한 번 선택된 변수를 제거하지 않음, 한 번 제거된 변수를 선택하지 않음”의 문제를 해결해 준다는 장점을 가지고 있습니다.

해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

Dimensionality Reduction

차원 축소(Dimensionality reduction)란 데이터가 가지고 있는 특성의 개수를 줄여나가면서 모델의 성능을 유지하는 방법입니다. 차원 축소를 하는 이유는 무엇일까요? 데이터 과학에서는 이른바 차원의 저주(Curse of dimensionality)라는 용어를 사용합니다. 차원의 저주가 의미하는 바는 다음과 같습니다.

“특성의 개수가 선형적으로 늘어날 때 동일한 설명력을 가지기 위해 필요한 인스턴스의 수는 지수적으로 증가한다. 즉 동일한 개수의 인스턴스를 가지는 데이터셋의 차원이 늘어날수록 설명력이 떨어지게 된다.”

아래 예시는 차원의 저주를 단적으로 보여주는 이미지입니다.

이미지 출처 : deepai.org

위 그림에는 총 20개의 인스턴스로 이루어진 데이터셋이 있습니다. 왼쪽부터 데이터셋이 각각 1차원, 2차원, 3차원 공간 속에 있을 때 인스턴스가 어떻게 위치하는 지를 나타내고 있습니다. 1차원(직선) 공간에 위치할 때에는 인스턴스들이 굉장히 조밀하게 배치되어 있슨 것을 알 수 있습니다. 이 중 몇몇 인스턴스는 2차원 공간에서 꽤 멀어지게 됩니다. 3차원 공간에서는 어떻게 될까요? 비록 위 그림에서 직관적으로 느껴지지는 않지만 아마 2차원에서 보다도 더욱 멀어질 것입니다. 이렇게 데이터의 차원이 커지면 인스턴스는 멀리 떨어져 있게 되고 데이터가 희소(Sparse)해지면서 설명력이 떨어지는 문제가 발생합니다.

하지만 데이터에게 중요한 본질적인 차원 수는 겉으로 드러나는 차원 수보다 더 적을 확률이 많습니다. MNIST 손글씨 데이터도 겉으로는 $768(=24 \times 24)$ 차원으로 구성된 데이터이지만 중간중간 데이터를 제거 하더라도 구분하는 데에는 큰 지장이 없습니다. 아래는 ISOMAP으로 MNIST 손글씨 데이터를 시각화하여 나타낸 것입니다. 이렇게 2차원으로 급격히 차원수를 줄이더라도 어느정도 분류되는 것을 볼 수 있습니다.

이미지 출처 : blog.paperspace.com

모든 특성이 독립이라는 가정이 있다면 특성의 개수가 늘어날수록 예측 모형의 성능은 증가해야 합니다. 하지만 현실적으로 이런 가정은 불가능 합니다. 게다가 고차원의 데이터에서는 변수에 포함될 노이즈의 합도 늘어나기 때문에 예측 모형의 성능이 점점 떨어지게 되는 문제도 발생합니다. 또한 모델을 생성할 때 행렬 연산을 해야하는데 차원이 커질수록 학습 시간이 늘어난다는 단점도 있습니다.

차원의 저주를 풀기 위한 방법 중 가장 간단한 것은 도메인 지식(Domain knowledge)을 활용하는 것입니다. 해당 분야에 대해 잘 알고 있는 사람이 데이터셋에서 중요도가 떨어지는 특성을 삭제하게 됩니다. 두 번째 방법은 만들고자 하는 모델의 목적 함수(Objective function)에 정규화(Regularization)를 사용하는 것입니다. 선형 회귀에 정규화를 사용하는 대표적인 방법으로 릿지(Ridge)와 라쏘(Lasso) 등이 있습니다. 마지막으로 기술적으로 차원의 수를 줄이는 방법을 사용하는 방법이 있습니다.

이런 차원 축소 방법을 사용하여 변수 간 상관관계를 줄일 수 있으며 중요한 정보를 유지하면서도 불필요한 정보를 줄일 수 있습니다. 게다가 데이터 후처리(Post-processing)을 간단히 할 수 있고 시각화(Visualization)도 가능하다는 장점이 있습니다.

Type of Dimensionality Reduction

Supervised vs Unsupervised

차원 축소는 크게 지도 학습(Supervised learning)을 기반으로 하는 방법과 비지도 학습(Unsupervised learning)을 기반으로 하는 방법으로 나눌 수 있습니다. 비지도 학습 기반에는 없었던 피드백 루프(Feedback loop)가 지도 학습 기반의 차원 축소에는 등장한다는 점에서 차이점을 가집니다.

지도 학습 기반의 차원축소에서는 이 피드백 루프를 통해서 가장 적합한 특성 조합을 찾을 때까지 알고리즘을 통해 반복 학습합니다. 아래는 지도 학습 기반의 차원 축소를 그림으로 나타낸 것입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

반대로 비지도 학습 기반의 차원 축소에는 피드백 루프가 없습니다. 비지도 학습 기반의 차원 축소를 사용하면 반복없이 하나의 메커니즘을 통해 특성의 수를 줄일 수 있습니다.

지도 학습의 기반의 차원축소 방식 중 유전 알고리즘 방식은 랜덤으로 난수를 선택하기 때문에 최종적으로 선택된 특성이 매번 달라질 수 있습니다. 하지만 비지도 학습 기반 방식은 동일한 데이터에 동일한 알고리즘을 적용한다면 항상 같은 결과를 보여준다는 특징을 가지고 있습니다. 아래는 비지도 학습 기반의 차원 축소를 그림으로 나타낸 것입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

Feature Selection vs Feature Extraction

차원 축소를 실행한 뒤에 나오는 특성의 결과가 어떤 지에 따라서도 차원 축소를 2가지로 나눌 수 있습니다. 첫 번째는 특성 선택(Feature selection)입니다. 특성 선택 방법에서는 전체 특성 중에서 유의미한 것으로 판단되는 특성의 부분 집합을 선택합니다. 특성 선택은 선택과 학습이 일어나는 시점에 따라 다시 두 가지 방법으로 나눌 수 있습니다. 필터(Filter)는 특성 선택과 모델의 학습이 독립적인 경우이며 래퍼(Wrapper)에서는 모델은 최적화하는 과정에서 동시에 변수 선택이 이루어집니다.

두 번째 차원 축소 방법인 특성 추출(Feature extraction)은 기존 특성의 조합을 통해서 새로운 특성을 만들어냅니다. 이 때 만들어진 새로운 특성은 데이터를 더욱 잘 나타내는 특성이 되며, 추출되어 나온 특성의 개수는 당연히 원래 특성의 개수보다 적습니다.

아래는 특성 선택과 특성 추출을 비교하여 나타낸 이미지입니다. 기존 데이터의 특성 $X_m (m = 1,\cdots,n)$ 에 대하여 특성 선택에서는 특성의 개수를 $n$보다 줄이는 방법을, 특성 추출에서는 기존 특성을 조합하여 새로운 특성 집합인 $Z$를 만드는 것을 볼 수 있습니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

아래는 차원 축소를 특성 선택과 특성 추출로 분류한 뒤 방법에 따라 한 번더 분류한 그림입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

우선 특성 선택 중 필터 방법은 알고리즘을 사용하지 않는 방법이며 정보 획득량(Information gain, IG)이나 오즈비(Odds ratio) 등의 수치를 사용하여 특성을 평가합니다. 래퍼 방법에서는 알고리즘을 사용합니다. 전진 선택법(Forward selection), 후진 제거법(Backward elimination), 유전 알고리즘(Genetic algorithm) 등이 이에 속합니다.

특성 추출은 어떤 것에 중점을 두느냐에 따라 세 가지로 나누어 볼 수 있습니다. 첫 번째는 분산을 최대한으로 보존하는 방법이며 주성분분석(Principle component analysis)이 이 방법에 속합니다. 두 번째는 인스턴스간의 거리 정보를 최대화하는 것으로 다차원 스케일링(Multidimensional scaling)이 있습니다. 마지막으로 잠재된 비선형 구조를 찾는 방법이 있습니다. 지역적 선형 임베딩(Locally linear embedding, LLE), ISOMAP, t-SNE 등이 모두 이에 속합니다.

본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 책을 참고하였습니다.

Sentiment Analysis

감성 분석(Sentiment Analysis)이란 텍스트에 들어있는 의견이나 감성, 평가, 태도 등의 주관적인 정보를 컴퓨터를 통해 분석하는 과정입니다. 자연어 데이터에 들어있는 감성을 분석하는 일은 오래 전부터 연구되어왔습니다. 그럼에도 언어가 가지고 있는 모호성 때문에 쉽지 않았던 것이 사실입니다. 아래의 예시를 통해 어떤 어려움이 있는 지 보도록 하겠습니다.

“Honda Accords and Toyota Camrys are nice sedans.” (혼다 어코드와 도요타 캠리는 좋은 세단이다.)

위 문장은 혼다와 도요타의 차종 각각에 대해서 긍정을 나타내고 있습니다. 하지만 추가적인 내용이 붙었을 때 이들에 대한 평가가 달라지는 경우도 있습니다. 아래 문장을 보도록 하겠습니다.

“Honda Accords and Toyota Camrys are nice sedans, but hardly the best car on the road. (혼다 어코드와 도요타 캠리는 좋은 세단이지만,도로에서 가장 좋은 차는 아니다.)”

위와 같은 추가 설명이 붙는다면 위 문장은 대상에 대해 긍정을 표하고자 하는 문장인지, 부정을 표하고자 하는 문장인지 파악하기 매우 어렵게 됩니다. 이러한 언어의 모호성은 감성 분석을 어렵게 하는 원인이 됩니다.

감성 분석이 사용되는 곳은 다양합니다. 기업 내부적으로는 고객 피드백, 콜센터 메시지 등과 같은 데이터를 분석하며 외부적으로는 기업과 관련된 뉴스나 SNS 홍보물 등에 달린 댓글의 긍/부정을 판단하는 곳에 사용되고 있습니다. 개인 단위에서는 영화를 보기 전에 리뷰를 참고하는 것과 같이 특정 제품이나 서비스를 이용할 지를 결정하는 데에 사용할 수 있습니다. (우리는 단지 머신러닝 방법론을 사용하지 않았을 뿐 은연중에 감성 분석을 하고 있습니다.) 이외에도 광고의 효율을 높이거나 특정 약품이 사람들에게 실제로 효과가 있는 지를 알아보는 데에도 사용할 수 있습니다.

Architecture

감성 분석은 크게 두 가지 단계로 이루어져 있습니다. 첫 번째 단계로 문서(문장)의 어떤 부분에 의견이 담겨있는 지를 정의(Opinion definition)합니다 . 그 다음으로는 첫 번째 단계를 통해 모아진 의견을 요약(Opinion summerization)하게 됩니다.

Opinion Definition

먼저 첫 번째 단계, 즉 문서에서 의견을 찾아내는 과정을 더 자세히 들여다 보도록 하겠습니다. 가장 먼저 해야하는 일은 분석에 필요한 4가지 요소를 찾는 것입니다. 4가지 요소란 분석 대상이 되는 개체(Entity)나 개체의 특성(Aspect/Feature), 개체에 대한 의견에 담겨있는 감성(Sentiment), 의견을 표현하는 주체(Opinion holders), 그리고 발화 시점(Time)입니다.

우리가 찾고자 하는 의견은 일반적으로 일반 의견(Regular opinions)과 비교 의견(Comparative opinions)의 2가지로 분류할 수 있습니다. 전자는 단일한 개체(혹은 개체의 특성)에 대해 의견을 표현한 것입니다. 이는 또 두 가지로 분류할 수 있습니다. “이 제품은 좋다” 와 같은 직접적인 의견(Direct opinions)과 “이 제품은 잘 작동한다” 와 같은 간접적인 의견(Indirect opinions)이 그것입니다. 비교 의견은 2개 이상의 대상을 언급하며 서로에 대한 의견을 나타내는 것입니다.

Elements

비교 의견은 2개 이상의 대상이 언급되므로 분석하기가 상당히 어렵습니다. 따라서 일반 의견에 한정하여 감성 분석에 필요한 요소에 대해서 알아보겠습니다. 일반 의견은 대상(Target)이 하나이므로 위에서 알아본 4가지 요소(대상, 감성, 주체, 시점)를 아래와 같이 나타낼 수 있습니다.

[(g_i, so_{ijk}, h_j, t_k)]

위 표현에서 $g_i$ 는 분석 대상, $h_i$ 는 발화 주체, $t_k$ 는 발화 시점을 나타냅니다. $so_{ijk}$ 는 $i$ 에 대해서 $k$ 시점에 $j$ 가 표현한 감성입니다. 분석 대상이 하나인 경우라도 개체에 관한 서술인지, 개체의 특성에 관하여 서술한 것인지를 구분하기 위해 $g$ 를 $e\text{ (entity)}$ 와 $a \text{ (aspect/feature)}$ 로 구분하여 나타내기도 합니다. 이런 경우 문장에서 의견을 정의할 때 아래의 5가지 요소를 분석 대상으로 놓게 됩니다.

[(e_i, a_{jl}, so_{ijkl}, h_j, t_k)]

위 다섯가지 요소를 활요하면 문장에서 의견을 나타내는 부분을 구조화 할 수 있습니다. 문장 뿐만 아니라 문서와 같이 긴 텍스트에 내포된 감정을 분류할 때에도 같은 요소를 추출하여 나타냅니다.

Flow chart

일반적인 감성 분석 시스템의 순서도는 아래와 같습니다.

이미지 출처 : http://www.ceine.cl

실제로 감성 분석을 수행할 때에는 요소의 개수를 줄이기 위해 “하나의 문서 내에서는 한 사람이 한 개체에 대해서만 즉시 평가한다.”고 가정합니다. 분석 대상인 리뷰나 고객 피드백 등은 발화자 자신이 사용한 제품에 대해서 평가하는 것이므로 위 가정을 제법 잘 만족합니다. 이 가정을 사용하면 5개의 요소에서 대상$(e,a)$, 발화자$(h)$, 발화시점$(t)$ 등을 무시할 수 있습니다. 그렇기 때문에 문서에서 드러나는 감성 표현만 잘 추출해도 분석할 수 있게 되는 것이지요.

Method

감성 분석의 방법론은 아래와 같이 나눌 수 있습니다. 크게는 어휘 기반(Lexicon-based)의 감성 분석과 머신러닝 기반(ML-based)의 감성 분석으로 나눌 수 있습니다. 각각의 방법은 더욱 세부적인 방법들로 나눌 수 있으며 최근에는 BERT와 같은 트랜스포머 계열 신경망 모델이 많이 사용되고 있습니다.

이미지 출처 : github.com/pilsung-kang

어휘 기반(Lexicon-based)의 감성 분석

Manual

먼저 어휘 기반의 감성 분석에 대해서 알아보겠습니다. 위 구조도에서도 알 수 있듯 어휘 기반의 감성 분석은 총 세 가지 세부 방법을 가지고 있습니다. 첫 번째는 모든 단어에 대한 감성 사전을 수동(Manual)으로 구축하는 방법입니다. 감성 사전이란 문서의 각 단어가 가지는 긍/부정의 정도를 -1(부정) 부터 1(긍정) 사이의 점수로 레이블링한 것입니다.

감성이 들어갈 수 있는 품사인 명사, 형용사, 동사 키워드를 추출한 뒤에 이들에 대한 긍/부정 레이블링을 진행합니다. 이렇게 구축된 감성 사전을 사용하면 개체에 따른 극성이나 긍/부정을 시각화할 수 있습니다. 그리고 연관어 분석을 통해서 어떤 단어가 해당하는 단어들과 같이 사용되었는지도 알 수 있습니다. 수동으로 감성 사전을 구축하는 방법은 한 번 수행하고나면 적용하기 쉽다는 장점이 있습니다. 하지만 도메인에 따라 사용하는 어휘가 달라지고 긍/부정 점수도 달라질 수 있기 때문에 모든 도메인에 적용할 수 있는 감성 사전을 구축하는 것이 매우 어렵다는 단점을 가지고 있습니다.

Dictionary-based

두 번째 방법은 사전 기반(Dictionary-based)의 접근법 입니다. 첫 번째 방법과의 차이는 매 분석마다 새로운 사전을 쓰는 것이 아니라 기존에 잘 구축되어 있는 외부 사전을 차용한다는 데에 있습니다. 이 방법은 외부 사전을 가져오기 때문에 수동으로 구축하지 않아도 되며 분석에 적용하기 쉽다는 장점도 가지고 있습니다. 하지만 이 방법 역시 도메인 확장성이 없다는 단점을 가지고 있습니다.

예를 들어, 영화 리뷰 데이터에서 “졸리다” 라는 단어는 부정적인 의미를 가지고 있습니다. 하지만, 침대 상품평 데이터라면 “졸리다” 라는 단어는 긍정적인 의미를 가지고 있겠지요. 이렇게 도메인에 따라 달라지는 단점이 있기 때문에 만약 차용하려는 사전이 적용하려는 데이터와 다른 도메인으로부터 생성된 것이라면 다시 생각해보아야 합니다.

Corpus-based

마지막은 해당 말뭉치에 맞는 적절한 감성 어휘를 재구축하는 말뭉치 기반(Corpus-based)의 접근 방법입니다. 이 방법은 이전 방법들의 단점인 도메인 의존성을 극복할 수 있지만 좋은 사전 구축을 위해서 많은 데이터(거대한 말뭉치)를 필요로 한다는 조건을 가지고 있습니다. 특정 말뭉치를 분석하는 경우에는 해당 단어가 사용되었을 때 문장의 긍/부정을 t-Test를 통해서 판단합니다.

머신러닝 기반(ML-based)의 감성 분석

머신러닝 기술이 발달하면서 어휘 기반의 감성 분석 방법보다는 머신러닝 모델 기반의 감성 분석이 많이 수행되고 있습니다. 특히 지도 학습(Supervised Learning) 기반의 방법이 많이 시도되고 있습니다.

Linear

그 중 하나는 회귀 분석을 통해 사전을 구축하는 방식입니다. 일반적으로 리뷰 데이터에는 평점을 부여하는데, 이렇게 평점을 레이블링 된 데이터에 회귀 분석 모델을 적용하여 각 단어에 대한 감성 사전을 구축합니다. 구축한 이후에는 교차 검증을 통해 감성 사전으로서의 타당한 성능을 지니는지를 평가합니다. 검증을 통해 구축한 사전의 성능이 확보된 후에는 새로운 문서에 대한 감성 분석을 수행할 수 있게 됩니다.

Semi-supervised

지도 학습과 비지도 학습의 중간인 준지도 학습(Semi-supervised Learning)을 통해 감성 사전을 구축하기도 합니다. 준지도 학습 기반의 방법은 2가지 세부 방법으로 나뉘게 됩니다. 첫 번째는 감성 그래프(Sentiment graph)를 이용하는 방식입니다. 고차원 단어를 저차원으로 임베딩한 후에 거리를 기반으로 각 단어 사이의 네트워크를 구축합니다. 감성 점수가 확실한 수 개의 단어를 미리 레이블링(Pre-labeled sentiment words)한 뒤에 공간상의 위치에 따라 나머지 단어의 감성 점수를 측정합니다. 아래는 감성 그래프를 적용했을 때 단어가 긍/부정으로 레이블링 되는 과정을 시각화한 것입니다.

이미지 출처 : github.com/pilsung-kang

위에서는 “좋다”, “짱”, “재밌다”, “훌륭하다” 등을 긍정으로 “거슬리다”, “억지”, “지루”, “아쉬움” 등을 부정으로, 그리고 “보다”, “감독”, “주인공”, “친구”, “카메라” 와 같이 중립으로 미리 레이블링 했습니다. 그리고 이들과의 관계로부터 나머지 단어의 감정 점수를 매기게 됩니다.

준지도 학습을 통한 두 번째 접근 방식은 자가 학습(Self-training)입니다. 이 방법 역시 감성 그래프 방법에서 했던 것과 같이 특정한 수 개의 단어는 미리 레이블링 되어 있습니다. 이 어휘로만 분류기를 학습한 뒤에 정답이 없는 어휘에 분류기를 적용하여 결과의 신뢰도가 높으면 정답으로 지정한 후에 학습기를 재학습하는 방식입니다. 아래는 자가 학습 방법을 이용한 감성 분석을 사용한 예를 시각화한 것인데 반복 학습 횟수가 늘어날수록 레이블링 되는 단어가 더 많은 것을 볼 수 있습니다.

이미지 출처 : github.com/pilsung-kang

Neural Network

2016년에는 RNTN(Recursive Neural Tensor Network) 방법이 제시되었습니다. 여기서의 R은 Recursive(재귀적인)를 나타내는 단어로 RNN에서 사용되는 Recurrent(순환하는)와는 다른 의미를 가지고 있습니다. RNTN은 두 가지 벤치마크 모델이 있습니다.

첫 번째는 RecursiveNN 입니다. 각 단어를 아래와 같이 구조적으로 나타낸 이후 각 단어를 구(Phrase)로 하나씩 결합하면서 감성이 어떻게 나타내는 지를 계속해서 학습합니다. 논문에서는 긍정과 부정을 25단계로구분하였으며 동일한 구에 댛서는 3명이 평가한 결과물의 평균을 사용하여 레이블링 하였습니다. 여기서 재귀적(Recursive)이라는 수식어를 사용하는 이유는 각 단어 혹은 구마다 동일한 가중치를 적용하기 때문입니다. 아래 이미지는 RecursiveNN이 진행되는 과정을 나타낸 것입니다. 이 때 첫 번째 구 $p_1$의 긍/부정을 판별할 때와 두 번째 구 $p_2$의 긍/부정을 판별할 때 동일한 함수 $g$ 를 사용하는 것을 볼 수 있습니다.

이미지 출처 : Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank

이 과정을 수식으로 나타내면 다음과 같습니다.

[y^{\text{word}} = \text{softmax}(W_s \cdot \text{word})
p_1 = f\bigg(W \begin{bmatrix} b \ c\end{bmatrix} \bigg), \quad p_2 = f\bigg(W \begin{bmatrix} a \ p_1 \end{bmatrix} \bigg)]

위 식에서 활성화 함수인 $f$ 는 일반적으로 $\tanh$ 가 사용되며 이 때 가중치인 $W$ 는 변하지 않습니다. 그리고 새로 만들어지는 구를 구성하는 단어 혹은 작은 구를 표현하는 벡터는 Concatenate된 후에 가중치와 내적하게 됩니다.

두 번째 벤치마크 모델은 MV-RNN(Matrix-Vector Recursive Neural Network) 입니다. 이 방법은 더 긴 문장의 문맥을 행렬에 저장하여 기존 RecursiveNN의 한계점을 해결하고자 합니다.

그리고 두 벤치마크 모델을 결합하여 텐서로 쌓아 나타낸 것이 바로 아래의 RNTN입니다. RNTN은 일반적으로 각각의 벤치마크 모델보다 성능이 더 좋습니다. 특히 아래 이미지와 같이 “but”으로 두 문장이 이어져 있거나 복잡한 부정 표현(High-level Negation)이 문장에 존재하는 경우에 기존 모델보다 훨씬 더 좋은 성능을 나타냅니다.

이미지 출처 : Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank

아래 내용은 파이썬 자료구조와 알고리즘 , 파이썬 공식문서 을 참조하여 작성하였습니다.

collections

collections 은 리스트(list), 튜플(tuple), 딕셔너리(dictionary) 등에 대한 확장 데이터 구조를 제공하는 파이썬 내장 모듈이다. collections 내에는

Counter

Counter (카운터)는 해시 가능한 객체를 카운팅하는 데에 특화된 서브클래스이다. 시퀀스 내에 있는 요소의 개수를 딕셔너리 형태로 반환한다.

from collections import Counter

seq1 = [1, 2, 3, 2, 1, 1, 2, 2, 4, 3]
Counter(seq1)

>>> Counter({1: 3, 2: 4, 3: 2, 4: 1})

Counter 내에도 다양한 메서드가 존재한다. 그 중 하나는 .most_common() 이다. 이 메서드는 자연수 값 N을 인자로 받는다. 이 메서드는 큰 value를 가지는 요소와 그 개수를 상위 N개 만큼 출력한다. 이를 활용하면 어떤 요소가 해당 자료형 내에 많은 지를 알 수 있다. 해당 문자열 혹은 시퀀스에 들어있는 요소의 종류 수와 같거나 그보다 클 경우에는 모든 요소에 대해 출력한다.

from collections import Counter

print(Counter('bibbidibobbidiboo').most_common(3))
print(Counter('bibbidibobbidiboo').most_common(7))

>>> [('b', 7), ('i', 5), ('o', 3)]
    [('b', 7), ('i', 5), ('o', 3), ('d', 2)]

.subtract() 는 해당 요소 개수의 차이를 구할 때 사용되는 메서드이다. 아래의 코드를 보며 이해해보자.

from collections import Counter

counter_bibbidi = Counter('bibbidibobbidiboo')
counter_banana = Counter('bananaboat')

print(counter_bibbidi)
print(counter_banana)

counter_bibbidi.subtract(counter_banana)

print(counter_bibbidi)

>>> Counter({'b': 7, 'i': 5, 'o': 3, 'd': 2})
    Counter({'a': 4, 'b': 2, 'n': 2, 'o': 1, 't': 1})
    Counter({'b': 5, 'i': 5, 'd': 2, 'o': 2, 't': -1, 'n': -2, 'a': -4})

'bibbidibobbidiboo' 에 포함된 요소의 개수를 카운터를 통해 나타내면 Counter({'b': 7, 'i': 5, 'o': 3, 'd': 2}) 이다. 'bananaboat' 에 포함된 요소의 개수를 카운터를 통해 나타내면 Counter({'a': 4, 'b': 2, 'n': 2, 'o': 1, 't': 1}) 이다. .subtract() 메서드는 한 카운터에서 다른 카운터를 빼는 연산을 수행한다. 전자에서 후자를 빼준 후 다시 원래의 카운터를 출력하면 연산이 수행된 이후의 결과가 나오는 것을 볼 수 있다.

deque

deque (데크)는 ‘Double Ended QUEue’ 의 줄임말로서 양쪽 끝에서 모두 큐(Queue)의 역할을 수행할 수 있는 자료구조이다. 일반적인 큐는 LIFO(Last In First Out) 이지만 deque는 말 그대로 양쪽 끝에서 추가와 삭제를 모두 수행할 수 있다. 파이썬이 기본적으로 제공하는 리스트는 리스트의 끝에서만 추가 .append() 와 삭제 .pop() 및 확장 extend() 을 할 수 있다. 하지만 deque에서는 .appendleft() 와 .popleft() , extendleft() 를 통해서 왼쪽에서도 작업을 수행할 수 있다.

from collections import deque

deq = deque(['c', 'd', 'e'])
deq.append('f')
deq.appendleft('b')
print(deq)

deq.pop()
print(deq)

deq.popleft()
print(deq)

>>> deque(['b', 'c', 'd', 'e', 'f'])
    deque(['b', 'c', 'd', 'e'])
    deque(['c', 'd', 'e'])

위 코드에서 .appendleft() 혹은 .popleft() 를 통해 왼쪽에서도 추가, 삭제 등의 작업을 수행하는 것을 볼 수 있다.

deque에서는 앞/뒤로 추가, 삭제가 자유롭기 때문에 요소를 순환시킬 수 있는 메서드인 .rotate() 도 제공하고 있다.

from collections import deque

deq = deque(['a', 'b', 'c', 'd', 'e'])
deq.rotate(3)
print(deq)

>>> deque(['c', 'd', 'e', 'a', 'b'])

리스트에서 사용되었던 메서드인 .remove() , reverse() , index() , insert() 등은 그대로 사용할 수 있다.

defaultdict

defaultdict 는 일반 딕셔너리와 달리 지정되지 않은 키의 값(value)을 자동으로 할당한다. 자동으로 할당되는 값의 자료형은 defaultdict를 선언하면서 지정해줄 수 있다. 아래의 코드를 보고 defaultdict가 동작하는 방식을 알 수 있다.

from collections import defaultdict

dDict_int = defaultdict(int)
print(dDict_int['key1'])

dDict_int['key2'] = 'value2'
print(dDict_int)

>>> 0
    defaultdict(<class 'int'>, {'key1': 0, 'key2': 'value2'})

defaultdict를 선언하면서 기본 자료형을 int 로 설정해주면 값을 지정해주지 않은 키에 대해 기본 값인 0을 알아서 할당하는 것을 볼 수 있다. int 가 아닌 다른 자료형을 사용할 수도 있다. 아래는 기본 자료형을 list 로 했을 때의 코드이다.

from collections import defaultdict

dataset = {(1,'a'), (2,'b'), (3,'c'), (2,'d'), (1,'e'), (3,'f')}
dDict_list = defaultdict(list)

for key, value in dataset:
    dDict_list[key].append(value)
    
print(dDict_list)

>>> defaultdict(<class 'list'>, {3: ['c', 'f'], 2: ['d', 'b'], 1: ['a', 'e']})

미리 각 키 1, 2, 3 에 해당하는 기본 값 [] 이 있으므로 .append() 만을 통해서 값(value)을 변경할 수 있다.

namedtuple

namedtuple 은 일반 튜플과 성능이 비슷하지만 튜플 항목(field)에 대해 이름이 지어져 있어서 인덱스가 아닌 이름으로도 접근할 수 있는 시퀀스 데이터 타입이다.

from collections import namedtuple

Student = namedtuple('Student', 'name score grade')
student1 = Student('Jackson', 91, 'A')

print(student1[1])
print(student1.score)
print(student1.grade)

>>> 91
    91
    'A'

일반적으로 튜플은 값을 변경할 수 없는 불변 자료형이다. 하지만 namedtuple 의 경우에는 ._replace 메서드를 활용하여 특정한 이름의 값을 변경하여 새로운 변수에 저장하거나 기존 변수에 저장하여 덮어씌울 수 있다.

from collections import namedtuple

Student = namedtuple('Student', 'name score grade')
student1 = Student('Jackson', 91, 'A')
student2 = student1._replace(score=95, grade='A+')
print(student2)
print(student2.grade)

>>> Student(name='Jackson', score=95, grade='A+')
    'A+'

OrderedDict

Orderdict (정렬 딕셔너리)는 요소가 입력되는 순서를 기억하는 딕셔너리이다.

from collections import OrderedDict

dataset = {(1,'a'), (2,'b'), (3,'c')}
ODict1 = OrderedDict(dataset)

for key in ODict:
    print(key, ODict[key])
    
>>> 1 'a'
    3 'c'
    2 'b'

키가 입력된 순서를 기억하여 추후에 값이 바뀌더라도 순서가 바뀌지 않는 것을 아래 코드에서 볼 수 있다.

ODict[1] = 'f'
print(ODict)

>>> OrderedDict([(1, 'f'), (3, 'c'), (2, 'b')])

파이썬 3.7 이후부터는 표준 딕셔너리도 입력된 순서를 보장한다. 그래서 해당 버전 이상의 파이썬을 사용하고 있다면 굳이 OrderedDict를 사용하지 않아도 된다.

dict1 = {1:'a', 2:'b', 3:'c'}
dict1[1] = 'f'
print(dict1)

>>> {1: 'f', 2: 'b', 3: 'c'}

본 포스트의 내용은 고려대학교 강필성 교수님의 강의 와 김기현의 자연어처리 딥러닝 캠프 , 밑바닥에서 시작하는 딥러닝 2 , 한국어 임베딩 책을 참고하였습니다.

RNN for Sentence Classification

순환 신경망(Recurrent Neural Network, RNN)을 사용하여 문서를 분류하는 방법도 있다. RNN에서는 토큰의 순서가 중요해진다. 각 자리에 있는 단어를 임베딩 벡터로 나타내 준 후에 각 단계마다의 은닉 상태(Hidden state)에 넣어주어 다음 단계로 보내준다. 마지막 토큰(End Token)이 들어왔을 때의 Hidden state는 모든 토큰의 정보를 가지고 있다. 이를 완전 연결 층(Fully Connected Layer)에 넘긴 후 소프트맥스를 사용하여 범주를 예측한다.

이미지 출처 : Text-Analytics Github

가장 단순한 RNN(Vanilla RNN)은 구조 특성상 문서를 분류할 때 뒷쪽에 위치하는 단어의 영향을 더 많이 받는다. 이런 현상은 기울기 소실(Gradient Vanishing)으로 인한 장기 의존성(Long-term Dependency) 등의 문제를 야기하는 원인이 된다. 이를 해결하기 위하여 과거 정보를 선택적으로 보존하기 위한 모델들이 고안되었다. RNN을 변형한 장단기 기억망(Long-Short Term Memory, LSTM)과 GRU(Gated Recurrent Unit) 등은 Hidden Node의 구조를 변형하여 기존에 발생하던 문제를 일부 해결할 수 있었다.

Hidden Node의 구조를 변형하는 방법 외에도 Hidden Layer를 변형하는 방법이 제시되었다. 첫 번째로 양방향(Bi-directional)으로 학습을 진행하여 한 쪽에서 정보가 소실되는 것을 보완하는 방법이 있다. 두 번째로는 아예 Hidden Layer를 여러 층(Multi-Layer)으로 쌓은 뒤 학습을 진행하는 방법이 제안되었다.

Various RNN Architecture

위에서 제시된 방법 외에도 문서 분류를 위해서 고안된 다양한 방법들이 있다.

첫 번째는 여러 데이터셋을 하나의 Hidden Layer에 처리하도록 하는 방법이다. 같은 Task를 수행하기 위한 여러가지 데이터셋을 학습시켜 모델의 성능을 향상시킨다는 아이디어를 바탕으로 하고 있다. 위 그림에서 볼 수 있듯 여러 개의 데이터셋을 사용하더라도 Hidden Node는 공유한다. 이 방법에서 입력 임베딩 벡터는 두 가지로 나뉜다. $x^m_t, x^n_t$ 은 특정태스크에 맞춰진(Task specific) 임베딩 벡터이고, $x^s_t$ 는 서로 공유하는(Shared) 임베딩 벡터이다. 이 두 가지 임베딩 벡터를 동시에 학습시켜 모델의 성능을 향상시키는 것이 이 방법의 목표이다.

이미지 출처 : Text-Analytics Github

두 번째는 동일한 임베딩 벡터를 사용하되 Hidden Layer를 2개로 구성하여 각 단게의 Hidden state가 다음 단계에 서로 영향을 주도록 하는 구조이다. 마지막은 Hidden Layer를 3개로 구성하여 각각의 임베딩 벡터가 2개 $(h^m_t, h^s_t) \text{or} (h^n_t, h^s_t)$ 에 영향을 주도록 한다. 그리고 Shared Hidden Layer $h^s_t$ 가 각각의 $h^m_t, h^n_t$ 에게 영향을 주어 성능을 높이고자 하는 방식이다. 아래는 두 번째(Coupled-Layer)와 세 번째(Shared-Layer)의 구조를 도식화한 것이다.

이미지 출처 : Text-Analytics Github

Attention

이전에도 등장했던 어텐션(Attention) 메커니즘은 특정 Task(여기서는 분류)를 수행하는 과정에서 중요한 역할을 하는 단어에 가중치를 부여하는 방식이다. 어텐션 메커니즘의 목적은 $C$ 라는 문맥 벡터(Context Vector)를 만드는 것이다. 일련의 과정을 통해 만들어진 Context Vector, $C$ 는 문서를 분류하는 시점에서 어떤 단어가 더 중요한 지를 알려주는 증거가 된다. $C$ 를 구하는 수식은 아래와 같으며 아래 식에서 $\alpha$ 는 가중치이고, $h$ 는 은닉 상태 벡터(Hidden state vector)이다.

[C = \sum^T_{i=1} \alpha_ih_i]

$\alpha$ 를 계산하기 위해 제안된 2가지 어텐션 메커니즘이 있다. 두 방법 모두 2015년에 제안된 방식인데 첫 번째는 Bahdanau가 제안하였고, 두 번째는 Luong이 제안하였다. Bahdanau의 방식은 가중치(Attention score)를 따로 학습시키는 방식이다. Luong의 방식은 별도의 가중치 학습 없이 현재 Hidden state와 Target state의 벡터 연산(예를 들면, 내적)을 통해서 구한다. 실험 결과 두 방법 사이에 유의미한 성능 차이기 없었기 때문에 좀 더 단순한 Luong의 것을 사용하는 것이 일반적이 되었다.

이미지 출처 : Text-Analytics Github

그렇다면 Luong 어텐션에 대해서 좀 더 자세히 알아보자. 일반적인 RNN에서는 해당 토큰 까지의 은닉 상태 벡터(Hidden state vector)인 $h_t$ 만을 넘겨주어 $\tanh h_t$다. 하지만 어텐션 메커니즘에서는 컨텍스트 벡터인 $c_t$ 와 $h_t$ 를 Concatenate 하여 구하게 된다. 아래는 어텐션을 적용한 은닉 상태 벡터 $\tilde{h_t}$ 를 수식으로 나타낸 것이다.

[\tilde{h_t} = \tanh (W_c [c_t,h_t])]

이렇게 구해진 벡터에 소프트맥스 함수를 취하여 해당 문장이 특정 클래스에 속할 확률을 구하게 된다.

위 계산을 위해서는 컨텍스트 벡터인 $c_t$ 를 구할 수 있어야 하고 이를 구하기 위해서는 가중치 값인 $\alpha_t$ 를 구할 수 있어야 한다. Luong 어텐션 메커니즘에서는 $\alpha_t$ 를 Hidden state vector $\bar{h_s}$ 와 Target state $h_t$ 벡터의 연산으로 구한다. 이를 수식으로 나타내면 아래와 같다.

[\text{score}(h_t, \bar{h_s}) = \begin{cases} h_t^T\bar{h_s} \ h_t^TW_\alpha\bar{h_s} \ v_a^T \tanh(W_c[c_t;h_t]) \end{cases}]

이렇게 구해진 연산값(score)에 소프트맥스 함수를 적용하여 가중치 $\alpha$ 를 구한다.

[\alpha_t(s) = \frac{\exp(\text{score}(h_t, \bar{h_s}))}{\sum_{s^\prime}\exp(\text{score}(h_t, \bar{h_s^\prime}))}]

이렇게 구해진 가중치와 Hidden state vector $\bar{h_s}$ 를 내적하면 Context vector $c_t$ 를 구할 수 있다.

[c_t = \bar{h_s} \alpha_t]

RNN for Document Classification

2016년에는 어텐션 메커니즘을 계층적으로 쌓아 문서를 분류하는 방법이 제시되었다. 계층적 어텐션 네트워크(Hierarchical Attention Network)는 문장에 대해 단어 단위로 RNN을 수행하여 분류를 진행한 뒤, 그 결과 다시 RNN에 입력하여 문서를 분류하는 방법이다. 계층적 어텐션 네트워크를 도식화하여 나타내면 아래와 같다.

이미지 출처 : Text-Analytics Github

첫 번째 단계에서는 단어 시퀀스를 양방향(Bi-directional)으로 인코딩하며 두 번째 단계에서는 단어 단계에서 어텐션을 적용한다. 문장 내 단어 단위의 어텐션이 끝나면 문서 내 문장의 시퀀스를 인코딩 하게 된다.(세 번째 단계) 이렇게 인코딩된 벡터에 문장 단계의 어텐션을 적용하여 마지막으로 문서를 분류하게 된다.(네 번째 단계)

논문에서는 첫 번째와 세 번째 단계에 사용되는 인코더로 Bi-directional GRU를 사용하였다. 아래는 GRU의 Hidden Node를 도식화하여 나타낸 것이다.

이미지 출처 : Text-Analytics Github

이 인코더는 정방향과 역방향의 Hidden state vector $\overrightarrow{h_t}, \overleftarrow{h_t}$ 를 만들어내고 두 벡터를 Concatenate하여 $h_t$ 를 만들게 된다. 이렇게 구해진 $h_t$ 는 활성화 함수 $\tanh$ 를 거친 뒤 어텐션 $\alpha_t$ 을 적용하여 문장의 컨텍스트 벡터 $s$ 를 만든다.

이렇게 구해진 $s_i$ ( $i$ 번째 문장에서의 $s$ )에 다시 양방향 GRU를 적용하여 $\overrightarrow{h_i}, \overleftarrow{h_i}$ 를 구하고 두 벡터를 Concatenate하여 $h_i$ 를 만든다. 이렇게 구해진 $h_i$ 는 활성화 함수 $\tanh$ 를 거친 뒤 어텐션 $\alpha_i$ 을 적용하여 문장의 컨텍스트 벡터 $v$ 를 만든다. 이 $v$ 를 완전 연결층에 통과시킨 후 소프트맥스를 취하여 문서가 특정 클래스에 구할 확률을 구해낸다.

CNN vs RNN for Classfication

아래는 Localization을 통해 CNN과 RNN에서 긍정과 부정으로 문서를 분류하는 데 큰 영향을 끼친 단어들을 시각화한 것이다.

이미지 출처 : Text-Analytics Github

위 결과를 보면 CNN은 영향을 미치는 구(Phrase)를 좀 더 잘 판별하고 있음을 알 수 있다. CNN은 Window 크기에 따라 한 번에 수 개의 단어를 탐지하므로 이렇게 판단한다는 것을 알 수 있다. 반면에 RNN은 단어 하나씩을 듬성듬성 골라내고 있는 것을 알 수 있다.