소프트 마진(Soft Margin) SVM
13 Mar 2021 | Machine-Learning
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
Soft Margin SVM
이번에는 소프트마진 서포트 벡터 머신에 대해서 알아보도록 하겠습니다. 하드 마진 분류기가 보여준 것처럼 모든 데이터를 깨끗하게 두 쪽낼 수 있다면 좋겠지만 실제의 데이터는 그렇게 호락호락하지 않습니다. 실제로 맞닥뜨리는 데이터에는 항상 소음(Noise)이 있기 때문이지요.
보통의 데이터는 아래와 같은 모습입니다. 자신이 속하는 클래스의 마진 평면 밖으로 넘어간 인스턴스(1)가 있거나 심지어는 상대방 클래스의 마진 평면 너머로 넘어간 인스턴스(2)도 있지요. 이렇게 마진 평면을 넘어가는 인스턴스를 허용하는 서포트 벡터 머신을 소프트 마진 서포트 벡터 머신(Soft-margin SVM)이라고 합니다.
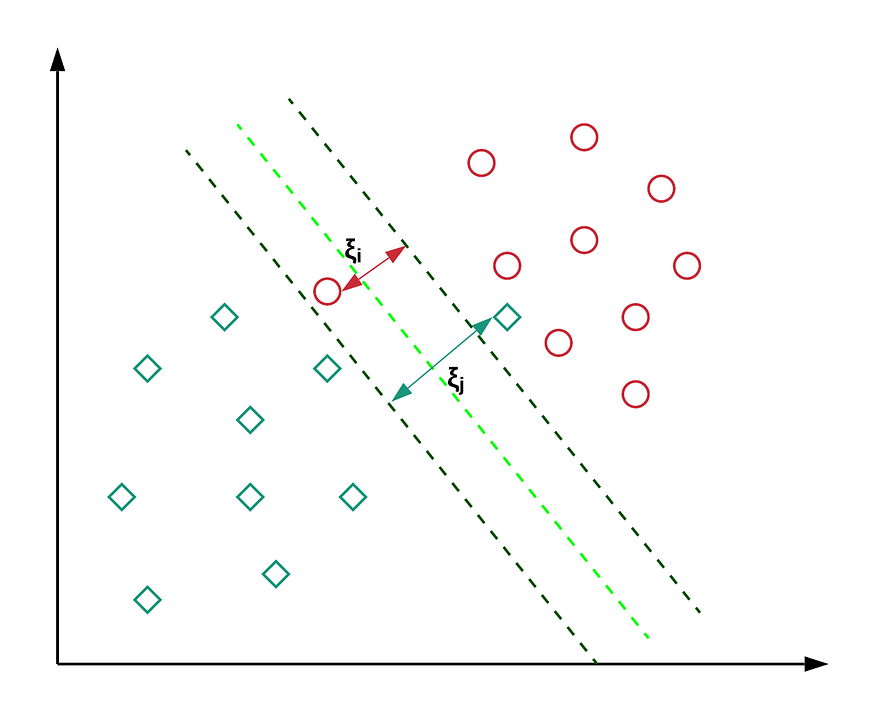
이미지 출처 : towardsdatascience.com
소프트마진 방법을 사용할 때에는 마진 평면을 넘어가는 인스턴스에 대해서 페널티(Panelty, $\xi$)를 부여합니다. 페널티는 자신이 속한 클래스의 마진 평면에서 떨어진 거리만큼 부여됩니다.
C-SVM
C-SVM의 목적 함수는 다음과 같습니다.
\(\min \frac{1}{2}\Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^N \xi_i \\
s.t. \quad y_i(\mathbf{w}^T\mathbf{x}_i+b) \geq 1 - \xi_i, \quad \xi_i>0, \quad \mu_i > 0, \quad \forall i\)
마진 평면을 넘어가는 즉, $\xi > 0$ 인 인스턴스에 대해서 $y_i(\mathbf{w}^T\mathbf{x}i+b) \geq 1 - \xi$ 식을 만족해야 합니다. 이런 제약조건 하에서 마진의 역수에 각 인스턴스의 오차 $\sum^N{i=1} \xi_i$ 를 더해준 값을 최소화하는 $\mathbf{w}, b, \xi_i$ 를 찾는 것이 목적입니다. $C$ 는 얼마나 강한 페널티를 줄 지를 결정하는 하이퍼파라미터입니다.
Optimization
하드 마진 때와 같이 라그랑주 승수법을 사용하여 최적화 문제를 풀 수 있습니다. 제약식까지 포함하여 나타낸 원초(primal) 문제는 다음과 같습니다.
\(\min L_p(\mathbf{w}, b, \alpha_i) = \frac{1}{2}\Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^N \xi_i - \sum_{i=1}^N \alpha_i(y_i(\mathbf{w}^T\mathbf{x}_i+b)-1+\xi_i) - \sum_{i=1}^N \mu_i\xi_i \\
s.t.\quad \alpha_i \geq 0\)
이제 KKT 조건을 적용하여 최저일 때의 조건을 구해보겠습니다.
\[\begin{aligned}
\frac{\partial L_p}{\partial \mathbf{w}} = 0 \quad &\Rightarrow \quad \mathbf{w} = \sum^N_{i=1} \alpha_iy_i\mathbf{x}_i \\
\frac{\partial L_p}{\partial b} = 0 \quad &\Rightarrow \quad \sum^N_{i=1}\alpha_iy_i = 0 \\
\frac{\partial L_p}{\partial \xi_i} = 0 \quad &\Rightarrow \quad C - \alpha_i-\mu_i = 0
\end{aligned}\]
조건을 활용하여 원초 문제를 쌍대 문제로 변형할 수 있습니다. 원초 문제에 KKT 조건에서 도출된 세 식을 각각 대입해주면 됩니다.
\[\begin{aligned}
\max L_D(\alpha_i) &= \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j + \sum_{i=1}^N (\alpha_i+\mu_i)\xi_i \\ &\quad - \sum_{i=1}^N \sum_{j=1}^N \alpha_i(y_i(\alpha_jy_j\mathbf{x}_i^T\mathbf{x}_j+b)-1+\xi_i) - \sum_{i=1}^N \mu_i\xi_i \\
&= \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \color{blue}{\alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j} + \sum_{i=1}^N (\color{magenta}{\alpha_i\xi_i}+\color{olive}{\mu_i\xi_i}) \\ &\quad - \sum_{i=1}^N \sum_{j=1}^N (\color{blue}{\alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j}+b \cdot \color{red}{\alpha_iy_i}-\alpha_i+\color{magenta}{\alpha_i\xi_i}) - \color{olive}{\sum_{i=1}^N \mu_i\xi_i} \\
&= \sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j
\end{aligned}\\
s.t. \quad \sum_{i=1}^N \alpha_i y_i = 0, \quad 0 \leq \alpha_i \leq C\]
Regularization cost, C
정칙화(Regularization)의 정도를 결정하는 하이퍼파라미터 $C$ 에 대해 알아보도록 하겠습니다. $C$ 가 크면 클수록 목적 함수에서 오차 $\xi_i$ 의 영향력이 커지게 됩니다. 즉, $C$ 가 클 경우 마진 평면을 벗어나는 인스턴스가 조금만 생겨도 철저히 배제하려 하기 때문에 마진의 크기가 줄어들게 됩니다. 반대로 $C$ 가 작을 경우에는 마진 평면을 벗어나는 인스턴스에 대해 그다지 큰 영향을 받지 않으므로 상대적으로 큰 마진을 갖는 분류기가 만들어집니다.
아래는 각기 다른 $C$ 에 대해서 마진이 어떻게 달라지는 지를 나타낸 이미지입니다.

이미지 출처 : dinhanhthi.com
$C$ 가 커질수록 마진의 크기가 줄어드는 것을 확인할 수 있습니다.
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
Soft Margin SVM
이번에는 소프트마진 서포트 벡터 머신에 대해서 알아보도록 하겠습니다. 하드 마진 분류기가 보여준 것처럼 모든 데이터를 깨끗하게 두 쪽낼 수 있다면 좋겠지만 실제의 데이터는 그렇게 호락호락하지 않습니다. 실제로 맞닥뜨리는 데이터에는 항상 소음(Noise)이 있기 때문이지요.
보통의 데이터는 아래와 같은 모습입니다. 자신이 속하는 클래스의 마진 평면 밖으로 넘어간 인스턴스(1)가 있거나 심지어는 상대방 클래스의 마진 평면 너머로 넘어간 인스턴스(2)도 있지요. 이렇게 마진 평면을 넘어가는 인스턴스를 허용하는 서포트 벡터 머신을 소프트 마진 서포트 벡터 머신(Soft-margin SVM)이라고 합니다.

이미지 출처 : towardsdatascience.com
소프트마진 방법을 사용할 때에는 마진 평면을 넘어가는 인스턴스에 대해서 페널티(Panelty, $\xi$)를 부여합니다. 페널티는 자신이 속한 클래스의 마진 평면에서 떨어진 거리만큼 부여됩니다.
C-SVM
C-SVM의 목적 함수는 다음과 같습니다. \(\min \frac{1}{2}\Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^N \xi_i \\ s.t. \quad y_i(\mathbf{w}^T\mathbf{x}_i+b) \geq 1 - \xi_i, \quad \xi_i>0, \quad \mu_i > 0, \quad \forall i\)
마진 평면을 넘어가는 즉, $\xi > 0$ 인 인스턴스에 대해서 $y_i(\mathbf{w}^T\mathbf{x}i+b) \geq 1 - \xi$ 식을 만족해야 합니다. 이런 제약조건 하에서 마진의 역수에 각 인스턴스의 오차 $\sum^N{i=1} \xi_i$ 를 더해준 값을 최소화하는 $\mathbf{w}, b, \xi_i$ 를 찾는 것이 목적입니다. $C$ 는 얼마나 강한 페널티를 줄 지를 결정하는 하이퍼파라미터입니다.
Optimization
하드 마진 때와 같이 라그랑주 승수법을 사용하여 최적화 문제를 풀 수 있습니다. 제약식까지 포함하여 나타낸 원초(primal) 문제는 다음과 같습니다. \(\min L_p(\mathbf{w}, b, \alpha_i) = \frac{1}{2}\Vert \mathbf{w} \Vert^2 + C \sum_{i=1}^N \xi_i - \sum_{i=1}^N \alpha_i(y_i(\mathbf{w}^T\mathbf{x}_i+b)-1+\xi_i) - \sum_{i=1}^N \mu_i\xi_i \\ s.t.\quad \alpha_i \geq 0\)
이제 KKT 조건을 적용하여 최저일 때의 조건을 구해보겠습니다.
\[\begin{aligned} \frac{\partial L_p}{\partial \mathbf{w}} = 0 \quad &\Rightarrow \quad \mathbf{w} = \sum^N_{i=1} \alpha_iy_i\mathbf{x}_i \\ \frac{\partial L_p}{\partial b} = 0 \quad &\Rightarrow \quad \sum^N_{i=1}\alpha_iy_i = 0 \\ \frac{\partial L_p}{\partial \xi_i} = 0 \quad &\Rightarrow \quad C - \alpha_i-\mu_i = 0 \end{aligned}\]조건을 활용하여 원초 문제를 쌍대 문제로 변형할 수 있습니다. 원초 문제에 KKT 조건에서 도출된 세 식을 각각 대입해주면 됩니다.
\[\begin{aligned} \max L_D(\alpha_i) &= \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j + \sum_{i=1}^N (\alpha_i+\mu_i)\xi_i \\ &\quad - \sum_{i=1}^N \sum_{j=1}^N \alpha_i(y_i(\alpha_jy_j\mathbf{x}_i^T\mathbf{x}_j+b)-1+\xi_i) - \sum_{i=1}^N \mu_i\xi_i \\ &= \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \color{blue}{\alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j} + \sum_{i=1}^N (\color{magenta}{\alpha_i\xi_i}+\color{olive}{\mu_i\xi_i}) \\ &\quad - \sum_{i=1}^N \sum_{j=1}^N (\color{blue}{\alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j}+b \cdot \color{red}{\alpha_iy_i}-\alpha_i+\color{magenta}{\alpha_i\xi_i}) - \color{olive}{\sum_{i=1}^N \mu_i\xi_i} \\ &= \sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j \end{aligned}\\ s.t. \quad \sum_{i=1}^N \alpha_i y_i = 0, \quad 0 \leq \alpha_i \leq C\]Regularization cost, C
정칙화(Regularization)의 정도를 결정하는 하이퍼파라미터 $C$ 에 대해 알아보도록 하겠습니다. $C$ 가 크면 클수록 목적 함수에서 오차 $\xi_i$ 의 영향력이 커지게 됩니다. 즉, $C$ 가 클 경우 마진 평면을 벗어나는 인스턴스가 조금만 생겨도 철저히 배제하려 하기 때문에 마진의 크기가 줄어들게 됩니다. 반대로 $C$ 가 작을 경우에는 마진 평면을 벗어나는 인스턴스에 대해 그다지 큰 영향을 받지 않으므로 상대적으로 큰 마진을 갖는 분류기가 만들어집니다.
아래는 각기 다른 $C$ 에 대해서 마진이 어떻게 달라지는 지를 나타낸 이미지입니다.

이미지 출처 : dinhanhthi.com
$C$ 가 커질수록 마진의 크기가 줄어드는 것을 확인할 수 있습니다.

Comments