ISOMAP & 지역적 선형 임베딩(Locally Linear Embedding, LLE)
06 Oct 2020 | Machine-Learning
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
ISOMAP
이전에 알아본 주성분분석(PCA)과 다차원 척도법(MDS)은 알고리즘 내부 계산이 쉬울 뿐만 아니라 선형 구조를 가지는 데이터에 대해서 전역 최적점을 찾아낸다는 장점을 가지고 있습니다. 하지만 데이터가 비선형 구조를 가지고 있을 때에는 구조를 파악하지 못하여 두 방법을 사용하더라도 최적점을 찾아내지 못한다는 단점을 가지고 있습니다.
이번 시간에는 이런 문제를 해결할 수 있는, 즉 비선형 구조를 가진 데이터의 차원 축소를 위한 방법들에 대해서 알아보도록 하겠습니다. 첫 번째로 알아볼 방법은 ISOMAP(ISOmetric feature MAPping)입니다. ISOMAP은 다차원 척도법과 거의 유사하지만 인스턴스 사이의 거리(Distance)를 비선형 데이터 구조에 맞도록 계산해내는 단계에서 차이점을 가집니다.
특정 데이터셋의 구조가 아래 이미지와 같다고 해보겠습니다.
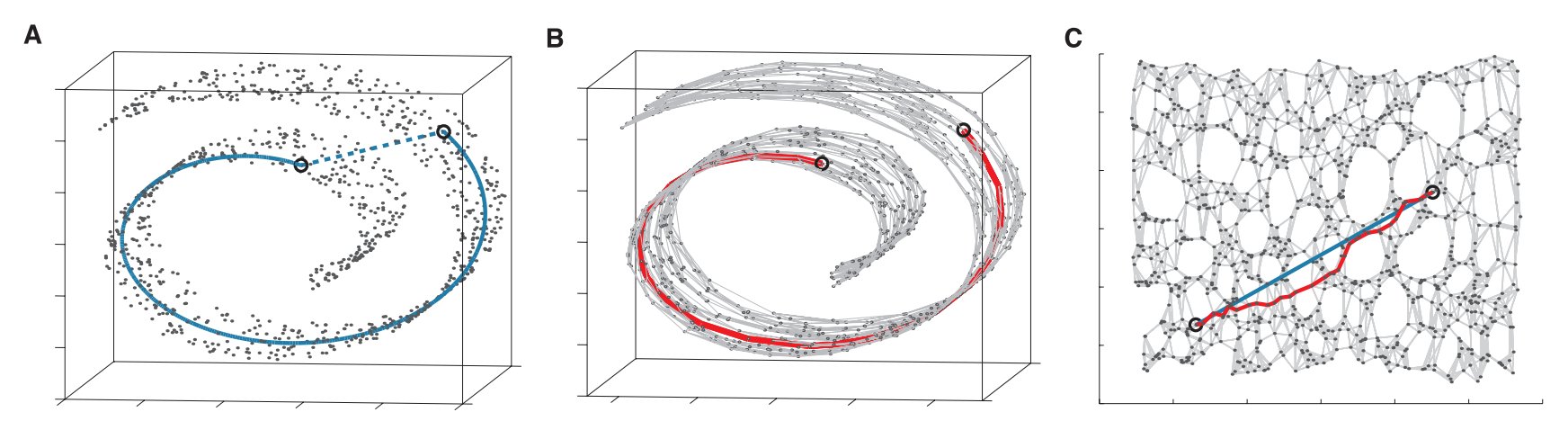
이미지 출처 : lovit.github.io
일반적인 다차원 척도법을 사용한다면 그림 A의 두 개 원이 가리키고 있는 두 인스턴스의 거리는 파란색 점선의 길이를 사용할 것입니다. 하지만 위와 같이 돌돌 말린(Swiss-roll) 데이터에서 두 점 사이의 실질적인 거리는 파란색 실선의 거리가 될 것입니다. 말려있는 데이터를 펼친 후에 두 인스턴스 사이의 거리인 것이지요.
위와 같이 데이터의 구조가 선형이 아니라 다양체(Manifold, 매니폴드)라면 각 인스턴스 사이의 거리를 다르게 정의해야 할 것입니다. ISOMAP은 이를 그래프(Graph) 구조로 해결하고자 하는 방법입니다. A에 있는 모든 인스턴스를 그래프 구조로 나타내면 B와 같이 변하게 됩니다. 그래프 구조에서는 최단 경로를 구하는 알고리즘이 이미 존재하므로 그래프 상에서 두 점 사이의 최단 경로를 구하여 실제 거리를 근사하게 됩니다. 그리고 이렇게 구해지는 각 인스턴스 사이의 거리가 ISOMAP에서의 거리가 됩니다.
Procedure
이제 ISOMAP이 어떤 과정을 통해 알고리즘을 수행하는지 알아보겠습니다. 인스턴스 사이의 거리를 구하는 것을 제외하고는 다차원 척도법과 동일한 계산과정을 거치기 때문에 간단한 편입니다.
첫 번째 단계는 각 인스턴스를 노드로 갖고 그 사이를 엣지로 연결하는 그래프 구조로 변형하는 것입니다. 연결하는 방법에 따라서 $\epsilon - \text{ISOMAP}$과 $k - \text{ISOMAP}$으로 나뉩니다. 전자는 일정한 기준 거리인 $\epsilon$을 설정한 후에 그보다 가까운 모든 인스턴스를 이웃 노드로 설정하여 연결합니다. 후자는 $k$개의 가장 가까운 인스턴스를 찾아 연결하는 방법입니다.
이렇게 모든 인스턴스를 연결했다면 두 번째 단계로 각 노드 사이의 최단 거리를 구하여 근접도(Proximity) 행렬을 만듭니다. 그래프 구조에서 노드 사이의 최단 경로를 구하는 알고리즘은 이미 알려져 있으므로 이 방법을 사용합니다.
마지막으로 이렇게 근접도 행렬을 구성한 이후에는 다차원 척도법에서 사용했던 방법을 사용하여 차원 축소를 수행할 수 있습니다.
Locally Linear Embedding
다음으로 알아볼 방법은 지역적 선형 임베딩(Locally Linear Embedding, LLE)입니다. 지역적 선형 임베딩은 고유벡터를 사용하는 방법으로 다루기가 쉽고 지역 최적점(Local optimum)에 빠지지 않을 수 있다는 장점을 가지고 있습니다. 비선형 임베딩 자체를 찾아내어 고차원 매니폴드 데이터를 저차원 데이터로 나타낼 수 있습니다. ISOMAP과 목적은 동일하지만 지역성(Locality)을 어떻게 수학적으로 반영하느냐에 따라서 지역적 선형 임베딩과 ISOMAP의 차이가 발생하게 됩니다.
Procedure
이어서 지역적 선형 임베딩이 수행하는 계산을 따라가 보겠습니다. 첫 번째 단계로 각 인스턴스의 이웃을 찾습니다. 다음 단계로는 각 인스턴스의 이웃으로부터 자기 자신을 재구축(reconstruct)할 수 있는 최적의 가중치 $W_{ij}$ 를 계산합니다. 수식으로 나타내면 아래의 목적 함수를 최소화하는 과정과 동일합니다.
\[E(\mathbf{W}) = \sum_i \big\vert \mathbf{x}_i - \mathbf{x}_i^\prime \big\vert^2 = \sum_i \big\vert \mathbf{x}_i - \sum_j\mathbf{W}_{ij}\mathbf{x}_j\big\vert^2\]
위 수식에서 $\mathbf{x}_i$ 는 재구축의 대상이 되는 원래의 인스턴스이며 그 뒤에오는 항은 이웃들과 가중치로부터 재구축한 $\mathbf{x}_i^\prime$ 입니다. 이 둘 사이의 차이를 줄이는 것이 목적이므로 평균 제곱 오차를 사용하여 나타낸 함수를 최소화하게 됩니다. 위 함수에서 가중치 값이 가지는 조건은 2가지 입니다. 첫 번째는 이웃이 아닌 인스턴스 $j$에 대해서는 가중치의 값이 0이라는 점이고, 두 번째는 모든 $i$마다 가중치의 합이 1이 된다는 점입니다. 수식으로는 아래와 같이 나타낼 수 있습니다.
\[\sum_jW_{ij} = 1 \quad \forall_i\]
이 최적화 문제를 모든 인스턴스 $i$에 대해서 풀어준 후에 나오는 가중치 행렬 $\mathbf{W}$는 지역성을 반영하는 행렬이 됩니다.
세 번째 단계로 이렇게 구한 가중치 $W$를 통해서 저차원에서 재구축한 인스턴스 $\mathbf{y}_i$를 최적화하는 문제를 풀게 됩니다. 수식으로 나타내면 아래와 같은 목적 함수를 최소화하는 과정이 됩니다.
\[\Phi(\mathbf{W}) = \sum_i \big\vert \mathbf{y}_i - \sum_j\mathbf{W}_{ij}\mathbf{y}_j\big\vert^2\]
이 세 단계를 그림으로는 아래와 같이 나타낼 수 있습니다.
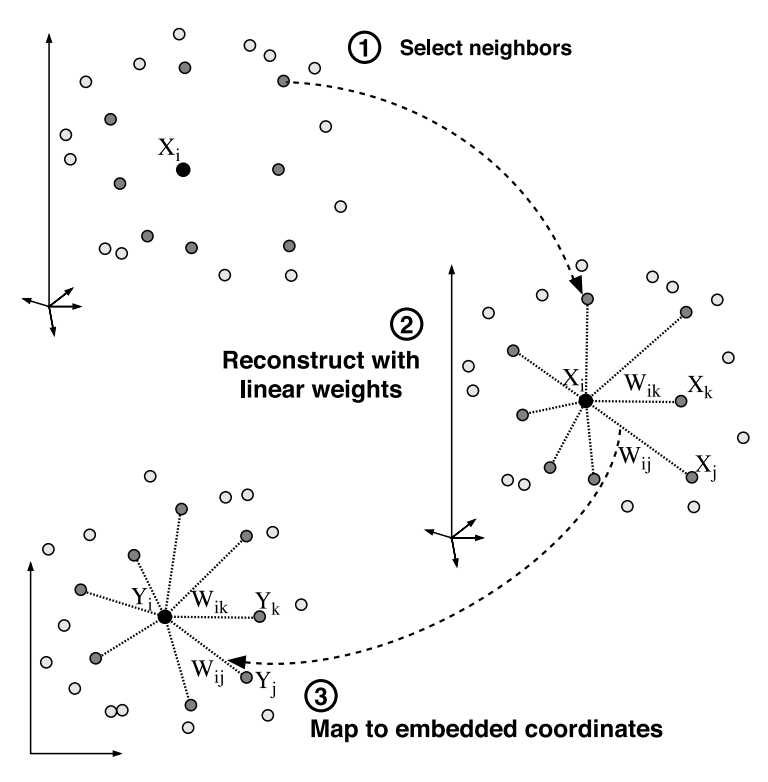
이미지 출처 : lovit.github.io
먼저 이웃을 찾게 되고, 찾은 이웃들로부터 자기 자신을 가장 잘 재구축 할 수 있는 가중치를 구해냅니다. 가중치를 구한 이후에는 이를 사용하여 저차원 공간상에서 다시 재구축해냅니다.
세 번째 단계는 구체적으로 아래와 같이 풀어낼 수 있습니다. 수식으로 나타낸 세 번째 단계의 목표는 아래와 같습니다.
\[\arg\min_y \Phi(\mathbf{W}) = \arg\min_y \sum_i \big\vert \mathbf{y}_i - \sum_j\mathbf{W}_{ij}\mathbf{y}_j\big\vert^2\]
$\arg\min$이후의 식을 행렬을 사용하여 아래와 같이 나타낼 수 있습니다.
\[\begin{aligned}
\sum_i \big\vert \mathbf{y}_i - \sum_j\mathbf{W}_{ij}\mathbf{y}_j\big\vert^2
&= \bigg[(\mathbf{I} - \mathbf{W})\mathbf{y}\bigg]^T(\mathbf{I}-\mathbf{W})\mathbf{y} \\
&= \mathbf{y}^T (\mathbf{I} - \mathbf{W})^T (\mathbf{I} - \mathbf{W}) \mathbf{y} \\
&= \mathbf{y}^T\mathbf{M}\mathbf{y}
\end{aligned}\]
$(\mathbf{I} - \mathbf{W})$은 이미 알고있는 값이므로 $\mathbf{M}$역시 구할 수 있습니다. 이 때 $\mathbf{y}$가 단위 벡터(Unit vector)라면 $\mathbf{y}^T\mathbf{y} = 1$ 조건을 만족하므로 라그랑주 승수법을 통해 구할 수 있습니다. 이 과정은 주성분 분석에서 $\mathbf{w}^T\mathbf{S}\mathbf{w}$의 최댓값을 구했던 과정과도 동일합니다.
주성분분석은 $\mathbf{w}^T\mathbf{w} = 1$ 조건에서 $\mathbf{w}^T\mathbf{S}\mathbf{w}$ 식의 최댓값을 구하는 것이었으므로 고윳값(Eigenvalue)이 큰 순서대로 $d$개를 뽑아 사용하였습니다. 하지만 지역적 선형 임베딩은 $\mathbf{y}^T\mathbf{y} = 1$ 조건에서 $\mathbf{y}^T\mathbf{M}\mathbf{y}$ 의 최솟값을 구하는 것이므로 고윳값이 작은 순서대로 사용하게 됩니다. 이 때 가장 아래의 고유벡터는 버리기 때문에 $d$차원으로 줄이기 위해서는 고윳값이 작은 순서대로 $d+1$개의 고유벡터를 추출하면 됩니다.
해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.
ISOMAP
이전에 알아본 주성분분석(PCA)과 다차원 척도법(MDS)은 알고리즘 내부 계산이 쉬울 뿐만 아니라 선형 구조를 가지는 데이터에 대해서 전역 최적점을 찾아낸다는 장점을 가지고 있습니다. 하지만 데이터가 비선형 구조를 가지고 있을 때에는 구조를 파악하지 못하여 두 방법을 사용하더라도 최적점을 찾아내지 못한다는 단점을 가지고 있습니다.
이번 시간에는 이런 문제를 해결할 수 있는, 즉 비선형 구조를 가진 데이터의 차원 축소를 위한 방법들에 대해서 알아보도록 하겠습니다. 첫 번째로 알아볼 방법은 ISOMAP(ISOmetric feature MAPping)입니다. ISOMAP은 다차원 척도법과 거의 유사하지만 인스턴스 사이의 거리(Distance)를 비선형 데이터 구조에 맞도록 계산해내는 단계에서 차이점을 가집니다.
특정 데이터셋의 구조가 아래 이미지와 같다고 해보겠습니다.

이미지 출처 : lovit.github.io
일반적인 다차원 척도법을 사용한다면 그림 A의 두 개 원이 가리키고 있는 두 인스턴스의 거리는 파란색 점선의 길이를 사용할 것입니다. 하지만 위와 같이 돌돌 말린(Swiss-roll) 데이터에서 두 점 사이의 실질적인 거리는 파란색 실선의 거리가 될 것입니다. 말려있는 데이터를 펼친 후에 두 인스턴스 사이의 거리인 것이지요.
위와 같이 데이터의 구조가 선형이 아니라 다양체(Manifold, 매니폴드)라면 각 인스턴스 사이의 거리를 다르게 정의해야 할 것입니다. ISOMAP은 이를 그래프(Graph) 구조로 해결하고자 하는 방법입니다. A에 있는 모든 인스턴스를 그래프 구조로 나타내면 B와 같이 변하게 됩니다. 그래프 구조에서는 최단 경로를 구하는 알고리즘이 이미 존재하므로 그래프 상에서 두 점 사이의 최단 경로를 구하여 실제 거리를 근사하게 됩니다. 그리고 이렇게 구해지는 각 인스턴스 사이의 거리가 ISOMAP에서의 거리가 됩니다.
Procedure
이제 ISOMAP이 어떤 과정을 통해 알고리즘을 수행하는지 알아보겠습니다. 인스턴스 사이의 거리를 구하는 것을 제외하고는 다차원 척도법과 동일한 계산과정을 거치기 때문에 간단한 편입니다.
첫 번째 단계는 각 인스턴스를 노드로 갖고 그 사이를 엣지로 연결하는 그래프 구조로 변형하는 것입니다. 연결하는 방법에 따라서 $\epsilon - \text{ISOMAP}$과 $k - \text{ISOMAP}$으로 나뉩니다. 전자는 일정한 기준 거리인 $\epsilon$을 설정한 후에 그보다 가까운 모든 인스턴스를 이웃 노드로 설정하여 연결합니다. 후자는 $k$개의 가장 가까운 인스턴스를 찾아 연결하는 방법입니다.
이렇게 모든 인스턴스를 연결했다면 두 번째 단계로 각 노드 사이의 최단 거리를 구하여 근접도(Proximity) 행렬을 만듭니다. 그래프 구조에서 노드 사이의 최단 경로를 구하는 알고리즘은 이미 알려져 있으므로 이 방법을 사용합니다.
마지막으로 이렇게 근접도 행렬을 구성한 이후에는 다차원 척도법에서 사용했던 방법을 사용하여 차원 축소를 수행할 수 있습니다.
Locally Linear Embedding
다음으로 알아볼 방법은 지역적 선형 임베딩(Locally Linear Embedding, LLE)입니다. 지역적 선형 임베딩은 고유벡터를 사용하는 방법으로 다루기가 쉽고 지역 최적점(Local optimum)에 빠지지 않을 수 있다는 장점을 가지고 있습니다. 비선형 임베딩 자체를 찾아내어 고차원 매니폴드 데이터를 저차원 데이터로 나타낼 수 있습니다. ISOMAP과 목적은 동일하지만 지역성(Locality)을 어떻게 수학적으로 반영하느냐에 따라서 지역적 선형 임베딩과 ISOMAP의 차이가 발생하게 됩니다.
Procedure
이어서 지역적 선형 임베딩이 수행하는 계산을 따라가 보겠습니다. 첫 번째 단계로 각 인스턴스의 이웃을 찾습니다. 다음 단계로는 각 인스턴스의 이웃으로부터 자기 자신을 재구축(reconstruct)할 수 있는 최적의 가중치 $W_{ij}$ 를 계산합니다. 수식으로 나타내면 아래의 목적 함수를 최소화하는 과정과 동일합니다.
\[E(\mathbf{W}) = \sum_i \big\vert \mathbf{x}_i - \mathbf{x}_i^\prime \big\vert^2 = \sum_i \big\vert \mathbf{x}_i - \sum_j\mathbf{W}_{ij}\mathbf{x}_j\big\vert^2\]위 수식에서 $\mathbf{x}_i$ 는 재구축의 대상이 되는 원래의 인스턴스이며 그 뒤에오는 항은 이웃들과 가중치로부터 재구축한 $\mathbf{x}_i^\prime$ 입니다. 이 둘 사이의 차이를 줄이는 것이 목적이므로 평균 제곱 오차를 사용하여 나타낸 함수를 최소화하게 됩니다. 위 함수에서 가중치 값이 가지는 조건은 2가지 입니다. 첫 번째는 이웃이 아닌 인스턴스 $j$에 대해서는 가중치의 값이 0이라는 점이고, 두 번째는 모든 $i$마다 가중치의 합이 1이 된다는 점입니다. 수식으로는 아래와 같이 나타낼 수 있습니다.
\[\sum_jW_{ij} = 1 \quad \forall_i\]이 최적화 문제를 모든 인스턴스 $i$에 대해서 풀어준 후에 나오는 가중치 행렬 $\mathbf{W}$는 지역성을 반영하는 행렬이 됩니다.
세 번째 단계로 이렇게 구한 가중치 $W$를 통해서 저차원에서 재구축한 인스턴스 $\mathbf{y}_i$를 최적화하는 문제를 풀게 됩니다. 수식으로 나타내면 아래와 같은 목적 함수를 최소화하는 과정이 됩니다.
\[\Phi(\mathbf{W}) = \sum_i \big\vert \mathbf{y}_i - \sum_j\mathbf{W}_{ij}\mathbf{y}_j\big\vert^2\]이 세 단계를 그림으로는 아래와 같이 나타낼 수 있습니다.

이미지 출처 : lovit.github.io
먼저 이웃을 찾게 되고, 찾은 이웃들로부터 자기 자신을 가장 잘 재구축 할 수 있는 가중치를 구해냅니다. 가중치를 구한 이후에는 이를 사용하여 저차원 공간상에서 다시 재구축해냅니다.
세 번째 단계는 구체적으로 아래와 같이 풀어낼 수 있습니다. 수식으로 나타낸 세 번째 단계의 목표는 아래와 같습니다.
\[\arg\min_y \Phi(\mathbf{W}) = \arg\min_y \sum_i \big\vert \mathbf{y}_i - \sum_j\mathbf{W}_{ij}\mathbf{y}_j\big\vert^2\]$\arg\min$이후의 식을 행렬을 사용하여 아래와 같이 나타낼 수 있습니다.
\[\begin{aligned} \sum_i \big\vert \mathbf{y}_i - \sum_j\mathbf{W}_{ij}\mathbf{y}_j\big\vert^2 &= \bigg[(\mathbf{I} - \mathbf{W})\mathbf{y}\bigg]^T(\mathbf{I}-\mathbf{W})\mathbf{y} \\ &= \mathbf{y}^T (\mathbf{I} - \mathbf{W})^T (\mathbf{I} - \mathbf{W}) \mathbf{y} \\ &= \mathbf{y}^T\mathbf{M}\mathbf{y} \end{aligned}\]$(\mathbf{I} - \mathbf{W})$은 이미 알고있는 값이므로 $\mathbf{M}$역시 구할 수 있습니다. 이 때 $\mathbf{y}$가 단위 벡터(Unit vector)라면 $\mathbf{y}^T\mathbf{y} = 1$ 조건을 만족하므로 라그랑주 승수법을 통해 구할 수 있습니다. 이 과정은 주성분 분석에서 $\mathbf{w}^T\mathbf{S}\mathbf{w}$의 최댓값을 구했던 과정과도 동일합니다.
주성분분석은 $\mathbf{w}^T\mathbf{w} = 1$ 조건에서 $\mathbf{w}^T\mathbf{S}\mathbf{w}$ 식의 최댓값을 구하는 것이었으므로 고윳값(Eigenvalue)이 큰 순서대로 $d$개를 뽑아 사용하였습니다. 하지만 지역적 선형 임베딩은 $\mathbf{y}^T\mathbf{y} = 1$ 조건에서 $\mathbf{y}^T\mathbf{M}\mathbf{y}$ 의 최솟값을 구하는 것이므로 고윳값이 작은 순서대로 사용하게 됩니다. 이 때 가장 아래의 고유벡터는 버리기 때문에 $d$차원으로 줄이기 위해서는 고윳값이 작은 순서대로 $d+1$개의 고유벡터를 추출하면 됩니다.

Comments