LSTM
26 Jun 2020 | Deep-Learning
본 포스트의 내용은 cs231n 강의자료 와 책 밑바닥에서 시작하는 딥러닝 2 를 참고하였습니다.
LSTM(Long Short Term Memory)
RNN에서의 장기 의존성 문제
RNN은 목표하고자 하는 단어가 멀리 떨어져 있을 때 기울기 소실 때문에 해당 단어를 학습하지 못하는 장기 의존성(Long-term dependency) 문제가 있었다. 이를 수식을 통해 좀 더 자세히 알아보자. RNN은닉층에서 일어나는 일을 편향(bias) 항을 제외하고 수식으로 나타내면 다음과 같이 나타낼 수 있다.
\[h_t = f_W (h_{t-1}, x_t)\\
h_t = \tanh (h_{t-1}W_h + x_tW_x)\]
$h_t$ 를 이전 단계의 $h$ 로 미분하면 다음과 같이 나타낼 수 있다.
\[\frac{\partial h_t}{\partial h_{t-1}} = \tanh^\prime (h_{t-1}W_h + x_tW_x)W_h\]
연쇄 법칙과 위 식을 활용하여 목표 시퀀스까지의 총 시간 $T$ 에 해당하는 출력값이 학습되는 과정을 다음과 같이 나타낼 수 있다.
\[\frac{\partial L_T}{\partial W} = \sum_{t=1}^T \frac{\partial L_t}{\partial W} \\
\frac{\partial L_T}{\partial W} = \frac{\partial L_T}{\partial h_T} \frac{\partial h_T}{\partial h_{T-1}} \cdots \frac{\partial h_1}{\partial W} = \frac{\partial L_T}{\partial h_T} \bigg(\prod^T_{t=2} \frac{\partial h_t}{\partial h_{t-1}} \bigg) \frac{\partial h_1}{\partial W} \\
\frac{\partial L_T}{\partial W} = \frac{\partial L_T}{\partial h_T} \bigg(\prod^T_{t=2} \tanh^\prime (h_{t-1}W_h + x_tW_x) \bigg) W_h^{T-1} \frac{\partial h_1}{\partial W}\]
위 식에서 괄호 안에 속해있는 부분 $\tanh^\prime (h_{t-1}W_h + x_tW_x)$ 은 $\tanh^\prime$ 의 특성에 따라 항상 0보다 같거나 작은 값을 나타낸다. (아래 그래프를 참조) 때문에 $T$ 가 커지면 그 값이 서로 곱해지면서 시퀀스에서 멀리 떨어진 토큰은 거의 학습되지 않는다. 이를 기울기 소실(Gradient Descent)이라고 한다.
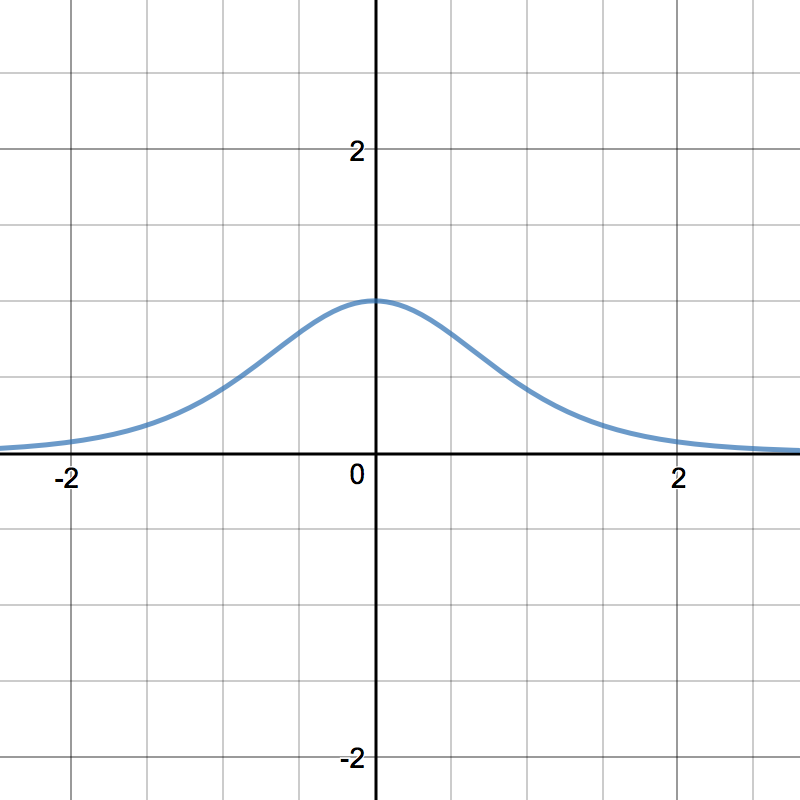
RNN의 활성화 함수(Activation function)인 tanh를 미분한 그래프이다. 최댓값이 1임을 알 수 있다.
이미지 출처 : ml-cheatsheet
LSTM (Long Short Term Memory)
장기 의존성 문제를 해결하고자 등장한 것이 LSTM(Long Short Term Memory)이다. 문제 해결을 위해 RNN의 구조를 변형해야 했고, 그리하여 게이트를 추가한 것이 바로 LSTM이다.
기본적인 형태의 RNN에는 입력 경로가 $h$ 하나 뿐이었지만, LSTM에서는 $c$ 라는 새로운 경로가 추가되었다. 아래는 LSTM의 계층이 동작하는 방식을 도식화하여 나타낸 것이다.

이미지 출처 : cs231n 강의자료
여기서 새로운 경로 $c$ 에는 시각 $t$ 에서 LSTM의 기억이 저장되어 있다. 이렇게 새로운 경로가 생긴 이유는 새로운 게이트(Gate)가 추가되었기 때문인데 각각의 게이트에 대해서 더 자세히 살펴보도록 하자.
출력 게이트(Output Gate) : LSTM계층의 출력값은 일련의 계산을 거쳐 나온 $c$ 에 활성화 함수를 취해준 $\tanh (c_t)$ 이다. 출력 게이트는 이 값을 다음 계층에 얼마나 허용해 줄 것인지(얼마나 영향을 미치도록 할 지)를 결정하는 게이트이다. 출력 게이트는 시그모이드(Sigmoid) 함수로 작동하는데 게이트가 작동하는 수식을 다음과 같이 나타낼 수 있다.
\[o = \sigma(x_tW_x^o + h_{t-1}W_h^o + b^o)\]
이렇게 구한 $o$ 값에 $\tanh(c_t)$ 를 원소별로 곱(아다마르 곱1)해주어 최종 출력값인 $h_t$ 를 구할 수 있게 된다. 수식으로는 다음과 같이 나타낼 수 있다.
\[h_t = o \circ \tanh(c_t)\]
망각 게이트(Forget Gate) : 이전 셀까지의 기억 $c_{t-1}$ 중 필요하지 않은 기억을 얼마나 지울 지를 결정하는 게이트이다. 망각 게이트 역시 시그모이드 함수를 통해 작동하며 수식으로는 다음과 같이 나타낼 수 있다.
\[f = \sigma(x_tW_x^f + h_{t-1}W_h^f + b^f)\]
이렇게 구해진 $f$ 값에 $c_{t-1}$ 과 아다마르 곱을 해주어 해당 셀까지의 기억인 $c_t$ 값의 일부를 구한다.
\[f \circ c_{t-1}\]
게이트 게이트(Gate gate) : 망각 게이트만 있다면 새로운 토큰 $x_t$ 로부터 오는 값은 영향을 많이 주지 못하게 된다. 때문에 새로운 정보를 만들어 낼 게이트가 필요한데 이를 $g$ 라고 한다. 이는 정보량을 조절하기 위한 것이 아니라 정보를 만들기 위한 것이므로 활성화 함수로 RNN과 동일한 $\tanh$ 를 사용하게 된다.
\[g = \tanh (x_tW_x^g + h_{t-1}W_h^g + b^g)\]
입력 게이트(Input Gate) : 새로 추가되는 정보가 얼마나 중요한지를 결정하는 게이트이다. $g$ 로부터 만들어진 값을 조절하므로 활성화 함수로 시그모이드 함수를 사용하며, 원소별 곱을 통해 $g$ 의 값을 조정하게 된다.
\[i = \sigma(x_tW_x^i + h_{t-1}W_h^i + b^i) \\
i \circ g\]
이 게이트들이 출력값 $c_t, h_t$ 에 영향을 미치는 과정을 다음과 같은 수식으로 나타낼 수 있다.
\[\left(\begin{array}{c} i \\ f \\ o \\ g \end{array}\right) = \left(\begin{array}{c} \sigma \\ \sigma \\ \sigma \\ \tanh \end{array}\right) W \left(\begin{array}{c} h_{t-1} \\ x_t\end{array}\right) \\
c_t = f \circ c_{t-1} + i \circ g \\
h_t = o \circ \tanh(c_t)\]
LSTM의 장점
LSTM은 어떻게 기울기 소실로 발생하는 장기 의존성 문제를 해결할 수 있는 것일까? LSTM의 역전파 과정을 살펴보자.

이미지 출처 : cs231n 강의자료
그림을 보면 $c$ 가 학습되는 과정에서는 $+$ 와 $\circ$ 노드만을 지난다는 것을 알 수 있다. $+$ 노드의 경우 동일한 기울기를 그대로 흘려주므로 아무리 개수가 많더라도 기울기를 소실시키지 않는다. 아다마르 곱이 있는 노드의 경우에는 행렬 곱보다 기울기를 덜 소실시키며, 아다마르 곱이 매번 다른 망각 게이트 값에 의해 결정되므로 곱셈의 효과가 누적되지 않는다는 장점이 있다. 망각 게이트의 값은 매번 동일한 값이 아니라 학습을 통해 변하기 때문에 기울기 소실이 적은 최적의 값을 적용할 수 있다.
-
크기가 같은 행렬을 각 원소의 행과 열에 맞추어 곱해주는 연산 위키피디아 : 아다마르 곱 ↩
본 포스트의 내용은 cs231n 강의자료 와 책 밑바닥에서 시작하는 딥러닝 2 를 참고하였습니다.
LSTM(Long Short Term Memory)
RNN에서의 장기 의존성 문제
RNN은 목표하고자 하는 단어가 멀리 떨어져 있을 때 기울기 소실 때문에 해당 단어를 학습하지 못하는 장기 의존성(Long-term dependency) 문제가 있었다. 이를 수식을 통해 좀 더 자세히 알아보자. RNN은닉층에서 일어나는 일을 편향(bias) 항을 제외하고 수식으로 나타내면 다음과 같이 나타낼 수 있다.
\[h_t = f_W (h_{t-1}, x_t)\\ h_t = \tanh (h_{t-1}W_h + x_tW_x)\]$h_t$ 를 이전 단계의 $h$ 로 미분하면 다음과 같이 나타낼 수 있다.
\[\frac{\partial h_t}{\partial h_{t-1}} = \tanh^\prime (h_{t-1}W_h + x_tW_x)W_h\]연쇄 법칙과 위 식을 활용하여 목표 시퀀스까지의 총 시간 $T$ 에 해당하는 출력값이 학습되는 과정을 다음과 같이 나타낼 수 있다.
\[\frac{\partial L_T}{\partial W} = \sum_{t=1}^T \frac{\partial L_t}{\partial W} \\ \frac{\partial L_T}{\partial W} = \frac{\partial L_T}{\partial h_T} \frac{\partial h_T}{\partial h_{T-1}} \cdots \frac{\partial h_1}{\partial W} = \frac{\partial L_T}{\partial h_T} \bigg(\prod^T_{t=2} \frac{\partial h_t}{\partial h_{t-1}} \bigg) \frac{\partial h_1}{\partial W} \\ \frac{\partial L_T}{\partial W} = \frac{\partial L_T}{\partial h_T} \bigg(\prod^T_{t=2} \tanh^\prime (h_{t-1}W_h + x_tW_x) \bigg) W_h^{T-1} \frac{\partial h_1}{\partial W}\]위 식에서 괄호 안에 속해있는 부분 $\tanh^\prime (h_{t-1}W_h + x_tW_x)$ 은 $\tanh^\prime$ 의 특성에 따라 항상 0보다 같거나 작은 값을 나타낸다. (아래 그래프를 참조) 때문에 $T$ 가 커지면 그 값이 서로 곱해지면서 시퀀스에서 멀리 떨어진 토큰은 거의 학습되지 않는다. 이를 기울기 소실(Gradient Descent)이라고 한다.

RNN의 활성화 함수(Activation function)인 tanh를 미분한 그래프이다. 최댓값이 1임을 알 수 있다.
이미지 출처 : ml-cheatsheet
LSTM (Long Short Term Memory)
장기 의존성 문제를 해결하고자 등장한 것이 LSTM(Long Short Term Memory)이다. 문제 해결을 위해 RNN의 구조를 변형해야 했고, 그리하여 게이트를 추가한 것이 바로 LSTM이다.
기본적인 형태의 RNN에는 입력 경로가 $h$ 하나 뿐이었지만, LSTM에서는 $c$ 라는 새로운 경로가 추가되었다. 아래는 LSTM의 계층이 동작하는 방식을 도식화하여 나타낸 것이다.

이미지 출처 : cs231n 강의자료
여기서 새로운 경로 $c$ 에는 시각 $t$ 에서 LSTM의 기억이 저장되어 있다. 이렇게 새로운 경로가 생긴 이유는 새로운 게이트(Gate)가 추가되었기 때문인데 각각의 게이트에 대해서 더 자세히 살펴보도록 하자.
출력 게이트(Output Gate) : LSTM계층의 출력값은 일련의 계산을 거쳐 나온 $c$ 에 활성화 함수를 취해준 $\tanh (c_t)$ 이다. 출력 게이트는 이 값을 다음 계층에 얼마나 허용해 줄 것인지(얼마나 영향을 미치도록 할 지)를 결정하는 게이트이다. 출력 게이트는 시그모이드(Sigmoid) 함수로 작동하는데 게이트가 작동하는 수식을 다음과 같이 나타낼 수 있다.
\[o = \sigma(x_tW_x^o + h_{t-1}W_h^o + b^o)\]이렇게 구한 $o$ 값에 $\tanh(c_t)$ 를 원소별로 곱(아다마르 곱1)해주어 최종 출력값인 $h_t$ 를 구할 수 있게 된다. 수식으로는 다음과 같이 나타낼 수 있다.
\[h_t = o \circ \tanh(c_t)\]망각 게이트(Forget Gate) : 이전 셀까지의 기억 $c_{t-1}$ 중 필요하지 않은 기억을 얼마나 지울 지를 결정하는 게이트이다. 망각 게이트 역시 시그모이드 함수를 통해 작동하며 수식으로는 다음과 같이 나타낼 수 있다.
\[f = \sigma(x_tW_x^f + h_{t-1}W_h^f + b^f)\]이렇게 구해진 $f$ 값에 $c_{t-1}$ 과 아다마르 곱을 해주어 해당 셀까지의 기억인 $c_t$ 값의 일부를 구한다.
\[f \circ c_{t-1}\]게이트 게이트(Gate gate) : 망각 게이트만 있다면 새로운 토큰 $x_t$ 로부터 오는 값은 영향을 많이 주지 못하게 된다. 때문에 새로운 정보를 만들어 낼 게이트가 필요한데 이를 $g$ 라고 한다. 이는 정보량을 조절하기 위한 것이 아니라 정보를 만들기 위한 것이므로 활성화 함수로 RNN과 동일한 $\tanh$ 를 사용하게 된다.
\[g = \tanh (x_tW_x^g + h_{t-1}W_h^g + b^g)\]입력 게이트(Input Gate) : 새로 추가되는 정보가 얼마나 중요한지를 결정하는 게이트이다. $g$ 로부터 만들어진 값을 조절하므로 활성화 함수로 시그모이드 함수를 사용하며, 원소별 곱을 통해 $g$ 의 값을 조정하게 된다.
\[i = \sigma(x_tW_x^i + h_{t-1}W_h^i + b^i) \\ i \circ g\]이 게이트들이 출력값 $c_t, h_t$ 에 영향을 미치는 과정을 다음과 같은 수식으로 나타낼 수 있다.
\[\left(\begin{array}{c} i \\ f \\ o \\ g \end{array}\right) = \left(\begin{array}{c} \sigma \\ \sigma \\ \sigma \\ \tanh \end{array}\right) W \left(\begin{array}{c} h_{t-1} \\ x_t\end{array}\right) \\ c_t = f \circ c_{t-1} + i \circ g \\ h_t = o \circ \tanh(c_t)\]LSTM의 장점
LSTM은 어떻게 기울기 소실로 발생하는 장기 의존성 문제를 해결할 수 있는 것일까? LSTM의 역전파 과정을 살펴보자.

이미지 출처 : cs231n 강의자료
그림을 보면 $c$ 가 학습되는 과정에서는 $+$ 와 $\circ$ 노드만을 지난다는 것을 알 수 있다. $+$ 노드의 경우 동일한 기울기를 그대로 흘려주므로 아무리 개수가 많더라도 기울기를 소실시키지 않는다. 아다마르 곱이 있는 노드의 경우에는 행렬 곱보다 기울기를 덜 소실시키며, 아다마르 곱이 매번 다른 망각 게이트 값에 의해 결정되므로 곱셈의 효과가 누적되지 않는다는 장점이 있다. 망각 게이트의 값은 매번 동일한 값이 아니라 학습을 통해 변하기 때문에 기울기 소실이 적은 최적의 값을 적용할 수 있다.
-
크기가 같은 행렬을 각 원소의 행과 열에 맞추어 곱해주는 연산 위키피디아 : 아다마르 곱 ↩

Comments