합성곱 신경망(Convolutional Neural Network, CNN)
23 Mar 2020 | Deep-Learning
CNN
합성곱 신경망(Convolutional Neural Network, CNN)은 컴퓨터 비전(Computer vision)분야에서 특히 많이 쓰이는 신경망입니다. 합성곱 신경망이 주목을 받게 된 것도 2012년 이미지넷(ImageNet) 데이터셋을 분류하는 ILSVRC대회에서 우승한 AlexNet 덕분이었습니다.
이미지 분류에서 합성곱 신경망이 주목받게 된 이유는 무엇일까요? 이미지는 위치에 맞는 공간적인 특성을 가지고 있습니다. 하지만 일반적인 완전 연결층(Fully connected layer)은 모든 입력 값을 동등하게 취급하기 때문에 이런 공간적 특성을 잘 살려내지 못합니다. MNIST 손글씨 데이터를 완전 연결층으로 분류해본 분이라면 $(24,24)$ 데이터를 $(768,)$ 로 펼친 뒤에 신경망에 넣어본 적이 있을 것입니다. 물론 손글씨 데이터는 색상도 흑백인데다가 패턴이 간단하기 때문에 완전 연결 층으로도 꽤 좋은 분류기를 구현할 수 있습니다. 하지만 패턴이 복잡한 컬러 이미지를 이런 방식으로 분류하는 것은 쉬운일이 아닙니다.
반면 합성곱 신경망은 학습 과정에서 이런 공간적 특성을 보존하며 학습할 수 있습니다. 합성곱 층은 완전 연결 층과 달리 3차원 데이터를 입력받아 다시 3차원 데이터를 내놓습니다. 덕분에 층이 깊어지더라도 공간적 특성을 최대한 보존하며 학습할 수 있습니다.
Structure
합성곱 신경망의 구조가 어떻기에 이런 공간적 특성을 보존할 수 있는 것일까요? 먼저 합성곱 신경망의 구조를 살펴보겠습니다.

이미지 출처 : medium.com/@sdoshi579
합성곱 신경망은 크게 두 종류의 층으로 이루어져 있습니다. 하나는 위 그림에서 하늘색에 해당하는 합성곱 층(Convolutional layer)이고 나머지 하나는 주황색에 해당하는 풀링 층(Pooling layer)입니다. 마지막에는 분류를 위해 완전 연결 층을 하나 결합하여 사용합니다. 각 층에서 어떤 일이 일어나는지 하나씩 알아보도록 하겠습니다.
Conv Layer
합성곱 층은 입력 데이터에 특정 크기의 커널(Kernal matrix)을 적용하여 새로운 출력값을 계산하는 역할을 합니다. 아래 그림은 합성곱 층에서 입력 데이터로부터 합성곱 연산을 수행하는 과정을 나타낸 것입니다.

이미지 출처 : stackoverflow.com
커널은 왼쪽 위부터 시작하며 오른쪽 끝까지 행렬 원소끼리의 곱을 수행한 후에 다시 아래쪽 열 왼쪽부터 오른쪽으로 동일한 과정을 수행합니다. 커널에 있는 $0, -1, 5$와 같은 숫자는 파라미터이며 학습을 통해서 갱신됩니다. 합성곱 신경망에는 커널 외에도 편향을 적용할 수 있습니다. 커널과의 합성곱을 통해 나온 행렬의 모든 원소에 편향을 더하여 적용합니다. 합성곱 층에는 커널의 크기 외에도 옵션으로 적용할 수 있는 패딩과 스트라이드가 있습니다. 먼저 패딩의 역할부터 알아보겠습니다.
패딩(Padding)은 위 예시에서 볼 수 있는 것처럼 입력 데이터 주변을 특정 값으로 채우는 것을 패딩이라고 합니다. 위 예시에서는 값이 0이고 폭이 1인 패딩이 적용되었습니다. $1 \times 1$ 보다 큰 크기의 커널을 사용하면 합성곱 연산의 특성상 입-출력 크기가 많이 달라집니다. 패딩은 이런 크기 변화를 완화해주는 역할을 합니다. 위 예시에서도 폭이 1인 패딩을 사용하지 않았다면 출력되는 행렬의 크기는 $5 \times 5$ 가 아니라 $3 \times 3$ 으로 줄어들 것입니다. 패딩은 행렬 바깥에 특정한 값을 둘러줌으로써 이미지 가장자리 부분의 특성을 보존할 수 있다는 장점이 있습니다.
스트라이드(Stride)는 필터를 적용하는 위치의 간격입니다. 위에서 살펴본 예시에서는 스트라이드가 $1$로 오른쪽으로 $1$칸씩 이동하면서 합성곱을 수행한 뒤에 $1$칸 아래로 이동하여 같은 과정을 반복합니다. 스트라이드가 $2$이면 오른쪽으로 $2$칸씩 이동하면서 합성곱을 수행하고 오른쪽 끝에 닿으면 $2$칸 아래로 이동하여 같은 과정을 반복하게 됩니다.
패딩은 합성곱의 대상이 되는 행렬을 확장해주는 반면, 스트라이드는 일정 간격으로 합성곱을 건너뜁니다. 이 때문에 패딩을 늘리면 출력 크기가 늘어나게 되고, 스트라이드를 늘리면 출력 크기는 줄어들게 됩니다. 입력 데이터의 높이와 너비를 각각 $H, W$라 하고 커널의 높이와 너비를 $KH, KW$ 그리고 패딩과 스트라이드를 각각 $P, S$ 라 하면 출력 데이터의 크기는 아래와 같은 수식을 통해 구할 수 있습니다.
\[OH = \frac{H+2P-FH}{S}+1 \qquad OW = \frac{W+2P-FW}{S}+1\]
위 예시에서 입력 데이터의 사이즈는 $5 \times 5$ 이며 커널의 크기는 $3 \times 3$ 이었습니다. 패딩은 $1$이 적용되었고 스트라이드도 $1$이므로 아래 수식을 통해서 출력 데이터의 크기를 구할 수 있습니다.
\[OH = \frac{5+2\cdot 1-3}{1}+1=5 \qquad OW = \frac{4+2\cdot 1-3}{1}+1=5\]
위 수식으로 출력데이터의 크기 $5 \times 5$를 정확히 구해낼 수 있습니다.
with Channels
컬러 이미지인 경우에는 이미지의 차원이 더 늘어납니다. RGB값을 각각 적용하기 때문입니다. 이렇게 채널이 많아지는 경우에는 채널 갯수만큼의 커널을 각각 적용하여 병렬 연산을 한 뒤에 그 합을 출력데이터에 입력합니다. 아래의 그림은 3개의 채널로 구성된 입력 데이터의 합성곱 연산이 수행되는 과정을 이미지로 나타낸 것입니다.

이미지 출처 : thelearningmachine.ai
Pooling Layer
풀링 층에서는 가로, 세로 방향의 공간을 줄이기 위한 풀링(Pooling)을 수행합니다. 풀링 방법에는 최대 풀링(Max pooling)과 평균 풀링(Average pooling)이 있습니다. 최대 풀링은 정해진 범위 내에서 가장 큰 값을 꺼내오는 방식이며 평균 풀링은 정해진 범위 내에 있는 모든 요소의 평균을 가져오는 방식입니다. 일반적으로 이미지를 처리할 때에는 각 부분의 특징을 최대로 보존하기 위해서 최대 풀링을 사용하고 있습니다. 아래 그림은 $2 \times 2$ 크기의 최대 풀링과 평균 풀링을 처리하는 과정을 비교하여 나타낸 것입니다.
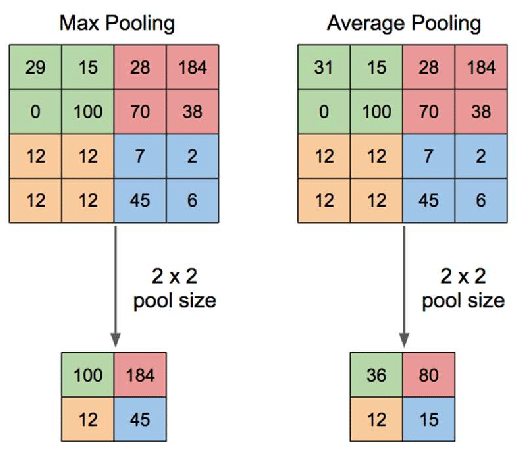
이미지 출처 : quora.com
위 그림에서 왼쪽은 최대 풀링으로 각각의 $2 \times 2$의 범위 내에서 가장 큰 요소인 $100, 184, 12, 45$ 출력 데이터로 가져옵니다. 오른쪽은 평균 풀링으로 각각의 $2 \times 2$의 범위 내 요소의 평균값인 $36, 80, 12, 15$ 를 출력 데이터로 가져옵니다. 풀링 층은 학습해야 할 매개변수가 없고 채널 수가 변하지 않으며 강건(Robust)하기 때문에 입력 변화에 영향을 적게 받는다는 특징을 가지고 있습니다.
Deep CNN
합성곱 신경망에서는 층을 깊게 쌓으면 어떤 이점이 있을까요? 각 합성곱 층마다 어떤 패턴을 학습하는 지를 시각화 해보면 신경망이 이미지를 어떤 방식으로 바라보는 지를 알 수 있습니다. 합성곱 신경망에서 연산이 일어나는 과정을 생각해보면 입력 데이터와 가까운 쪽의 합성곱 층은 이미지의 극히 일부 밖에 볼 수 없습니다. 하지만 층이 깊어지면 한 번에 이미지의 많은 부분을 볼 수 있습니다. 풀링 과정을 여러 번 거치면서 많은 픽셀 정보가 응축되기 때문입니다.
대표적인 합성곱 신경망 모델 중 하나인 알렉스넷(Alexnet)의 경우 1번째 합성곱 층에서는 엣지(Edge)나 블롭(Blob)등을 학습하고 3번째 층은 텍스쳐(Texture)를 학습합니다. 5번째 층에 다다르면 사물의 일부를 학습한다는 것으로 알려져 있습니다. 아래는 임의의 합성곱 신경망 내부에 있는 합성곱 층에서 학습하는 패턴을 시각화한 것입니다.

이미지 출처 : deeplizard.com
위 이미지는 입력 데이터와 가장 가까운 층으로 세로, 가로, 대각선 등의 엣지(Edge)를 학습하는 것을 알 수 있습니다.

이미지 출처 : deeplizard.com
위 이미지는 입력 데이터와 가장 멀리 떨어진 층, 즉 완전 연결 층과 연결된 합성곱 층으로 추상화된 사물의 형태를 패턴으로 학습하고 있는 것을 볼 수 있습니다.
CNN
합성곱 신경망(Convolutional Neural Network, CNN)은 컴퓨터 비전(Computer vision)분야에서 특히 많이 쓰이는 신경망입니다. 합성곱 신경망이 주목을 받게 된 것도 2012년 이미지넷(ImageNet) 데이터셋을 분류하는 ILSVRC대회에서 우승한 AlexNet 덕분이었습니다.
이미지 분류에서 합성곱 신경망이 주목받게 된 이유는 무엇일까요? 이미지는 위치에 맞는 공간적인 특성을 가지고 있습니다. 하지만 일반적인 완전 연결층(Fully connected layer)은 모든 입력 값을 동등하게 취급하기 때문에 이런 공간적 특성을 잘 살려내지 못합니다. MNIST 손글씨 데이터를 완전 연결층으로 분류해본 분이라면 $(24,24)$ 데이터를 $(768,)$ 로 펼친 뒤에 신경망에 넣어본 적이 있을 것입니다. 물론 손글씨 데이터는 색상도 흑백인데다가 패턴이 간단하기 때문에 완전 연결 층으로도 꽤 좋은 분류기를 구현할 수 있습니다. 하지만 패턴이 복잡한 컬러 이미지를 이런 방식으로 분류하는 것은 쉬운일이 아닙니다.
반면 합성곱 신경망은 학습 과정에서 이런 공간적 특성을 보존하며 학습할 수 있습니다. 합성곱 층은 완전 연결 층과 달리 3차원 데이터를 입력받아 다시 3차원 데이터를 내놓습니다. 덕분에 층이 깊어지더라도 공간적 특성을 최대한 보존하며 학습할 수 있습니다.
Structure
합성곱 신경망의 구조가 어떻기에 이런 공간적 특성을 보존할 수 있는 것일까요? 먼저 합성곱 신경망의 구조를 살펴보겠습니다.

이미지 출처 : medium.com/@sdoshi579
합성곱 신경망은 크게 두 종류의 층으로 이루어져 있습니다. 하나는 위 그림에서 하늘색에 해당하는 합성곱 층(Convolutional layer)이고 나머지 하나는 주황색에 해당하는 풀링 층(Pooling layer)입니다. 마지막에는 분류를 위해 완전 연결 층을 하나 결합하여 사용합니다. 각 층에서 어떤 일이 일어나는지 하나씩 알아보도록 하겠습니다.
Conv Layer
합성곱 층은 입력 데이터에 특정 크기의 커널(Kernal matrix)을 적용하여 새로운 출력값을 계산하는 역할을 합니다. 아래 그림은 합성곱 층에서 입력 데이터로부터 합성곱 연산을 수행하는 과정을 나타낸 것입니다.

이미지 출처 : stackoverflow.com
커널은 왼쪽 위부터 시작하며 오른쪽 끝까지 행렬 원소끼리의 곱을 수행한 후에 다시 아래쪽 열 왼쪽부터 오른쪽으로 동일한 과정을 수행합니다. 커널에 있는 $0, -1, 5$와 같은 숫자는 파라미터이며 학습을 통해서 갱신됩니다. 합성곱 신경망에는 커널 외에도 편향을 적용할 수 있습니다. 커널과의 합성곱을 통해 나온 행렬의 모든 원소에 편향을 더하여 적용합니다. 합성곱 층에는 커널의 크기 외에도 옵션으로 적용할 수 있는 패딩과 스트라이드가 있습니다. 먼저 패딩의 역할부터 알아보겠습니다.
패딩(Padding)은 위 예시에서 볼 수 있는 것처럼 입력 데이터 주변을 특정 값으로 채우는 것을 패딩이라고 합니다. 위 예시에서는 값이 0이고 폭이 1인 패딩이 적용되었습니다. $1 \times 1$ 보다 큰 크기의 커널을 사용하면 합성곱 연산의 특성상 입-출력 크기가 많이 달라집니다. 패딩은 이런 크기 변화를 완화해주는 역할을 합니다. 위 예시에서도 폭이 1인 패딩을 사용하지 않았다면 출력되는 행렬의 크기는 $5 \times 5$ 가 아니라 $3 \times 3$ 으로 줄어들 것입니다. 패딩은 행렬 바깥에 특정한 값을 둘러줌으로써 이미지 가장자리 부분의 특성을 보존할 수 있다는 장점이 있습니다.
스트라이드(Stride)는 필터를 적용하는 위치의 간격입니다. 위에서 살펴본 예시에서는 스트라이드가 $1$로 오른쪽으로 $1$칸씩 이동하면서 합성곱을 수행한 뒤에 $1$칸 아래로 이동하여 같은 과정을 반복합니다. 스트라이드가 $2$이면 오른쪽으로 $2$칸씩 이동하면서 합성곱을 수행하고 오른쪽 끝에 닿으면 $2$칸 아래로 이동하여 같은 과정을 반복하게 됩니다.
패딩은 합성곱의 대상이 되는 행렬을 확장해주는 반면, 스트라이드는 일정 간격으로 합성곱을 건너뜁니다. 이 때문에 패딩을 늘리면 출력 크기가 늘어나게 되고, 스트라이드를 늘리면 출력 크기는 줄어들게 됩니다. 입력 데이터의 높이와 너비를 각각 $H, W$라 하고 커널의 높이와 너비를 $KH, KW$ 그리고 패딩과 스트라이드를 각각 $P, S$ 라 하면 출력 데이터의 크기는 아래와 같은 수식을 통해 구할 수 있습니다.
\[OH = \frac{H+2P-FH}{S}+1 \qquad OW = \frac{W+2P-FW}{S}+1\]위 예시에서 입력 데이터의 사이즈는 $5 \times 5$ 이며 커널의 크기는 $3 \times 3$ 이었습니다. 패딩은 $1$이 적용되었고 스트라이드도 $1$이므로 아래 수식을 통해서 출력 데이터의 크기를 구할 수 있습니다.
\[OH = \frac{5+2\cdot 1-3}{1}+1=5 \qquad OW = \frac{4+2\cdot 1-3}{1}+1=5\]위 수식으로 출력데이터의 크기 $5 \times 5$를 정확히 구해낼 수 있습니다.
with Channels
컬러 이미지인 경우에는 이미지의 차원이 더 늘어납니다. RGB값을 각각 적용하기 때문입니다. 이렇게 채널이 많아지는 경우에는 채널 갯수만큼의 커널을 각각 적용하여 병렬 연산을 한 뒤에 그 합을 출력데이터에 입력합니다. 아래의 그림은 3개의 채널로 구성된 입력 데이터의 합성곱 연산이 수행되는 과정을 이미지로 나타낸 것입니다.

이미지 출처 : thelearningmachine.ai
Pooling Layer
풀링 층에서는 가로, 세로 방향의 공간을 줄이기 위한 풀링(Pooling)을 수행합니다. 풀링 방법에는 최대 풀링(Max pooling)과 평균 풀링(Average pooling)이 있습니다. 최대 풀링은 정해진 범위 내에서 가장 큰 값을 꺼내오는 방식이며 평균 풀링은 정해진 범위 내에 있는 모든 요소의 평균을 가져오는 방식입니다. 일반적으로 이미지를 처리할 때에는 각 부분의 특징을 최대로 보존하기 위해서 최대 풀링을 사용하고 있습니다. 아래 그림은 $2 \times 2$ 크기의 최대 풀링과 평균 풀링을 처리하는 과정을 비교하여 나타낸 것입니다.
이미지 출처 : quora.com
위 그림에서 왼쪽은 최대 풀링으로 각각의 $2 \times 2$의 범위 내에서 가장 큰 요소인 $100, 184, 12, 45$ 출력 데이터로 가져옵니다. 오른쪽은 평균 풀링으로 각각의 $2 \times 2$의 범위 내 요소의 평균값인 $36, 80, 12, 15$ 를 출력 데이터로 가져옵니다. 풀링 층은 학습해야 할 매개변수가 없고 채널 수가 변하지 않으며 강건(Robust)하기 때문에 입력 변화에 영향을 적게 받는다는 특징을 가지고 있습니다.
Deep CNN
합성곱 신경망에서는 층을 깊게 쌓으면 어떤 이점이 있을까요? 각 합성곱 층마다 어떤 패턴을 학습하는 지를 시각화 해보면 신경망이 이미지를 어떤 방식으로 바라보는 지를 알 수 있습니다. 합성곱 신경망에서 연산이 일어나는 과정을 생각해보면 입력 데이터와 가까운 쪽의 합성곱 층은 이미지의 극히 일부 밖에 볼 수 없습니다. 하지만 층이 깊어지면 한 번에 이미지의 많은 부분을 볼 수 있습니다. 풀링 과정을 여러 번 거치면서 많은 픽셀 정보가 응축되기 때문입니다.
대표적인 합성곱 신경망 모델 중 하나인 알렉스넷(Alexnet)의 경우 1번째 합성곱 층에서는 엣지(Edge)나 블롭(Blob)등을 학습하고 3번째 층은 텍스쳐(Texture)를 학습합니다. 5번째 층에 다다르면 사물의 일부를 학습한다는 것으로 알려져 있습니다. 아래는 임의의 합성곱 신경망 내부에 있는 합성곱 층에서 학습하는 패턴을 시각화한 것입니다.

이미지 출처 : deeplizard.com
위 이미지는 입력 데이터와 가장 가까운 층으로 세로, 가로, 대각선 등의 엣지(Edge)를 학습하는 것을 알 수 있습니다.

이미지 출처 : deeplizard.com
위 이미지는 입력 데이터와 가장 멀리 떨어진 층, 즉 완전 연결 층과 연결된 합성곱 층으로 추상화된 사물의 형태를 패턴으로 학습하고 있는 것을 볼 수 있습니다.

Comments