해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

t-SNE

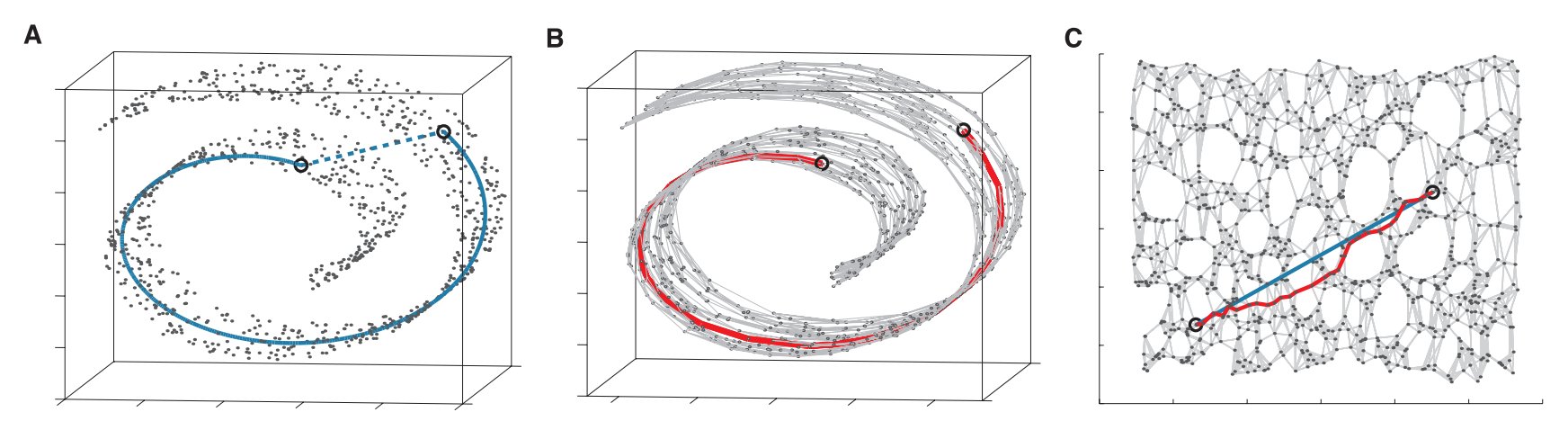
t-SNE(t-Stochastic Neighbor Embedding, t-확률적 이웃 임베딩)은 ISOMAP, 지역적 선형 임베딩(Locally Linear Embedding, LLE)과 더불어 많이 사용되는 비선형 구조 데이터를 차원 축소하는 알고리즘입니다.

Stochastic Neighbor Embedding

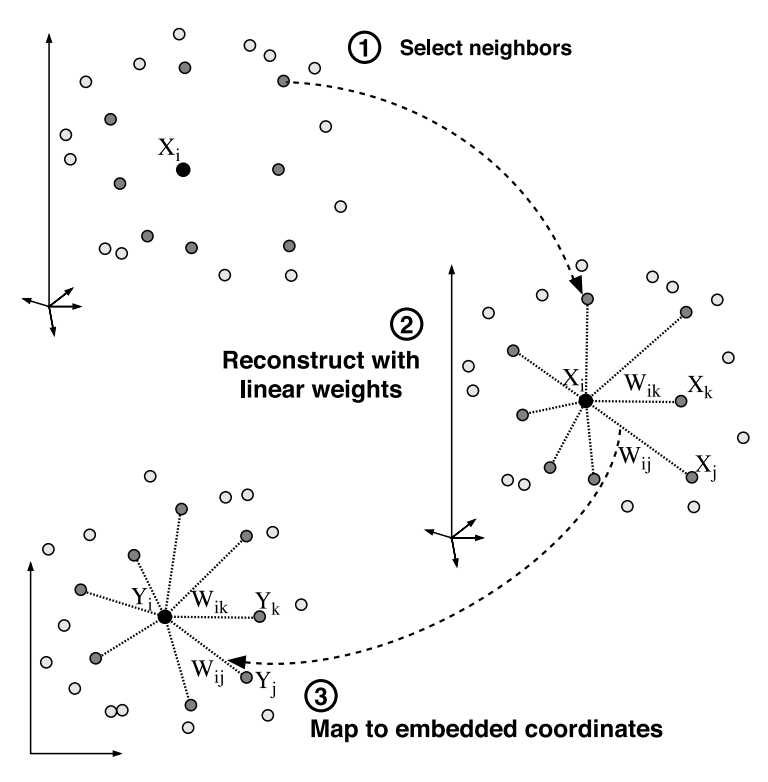
t-SNE의 핵심이 되는 SNE(Stochastic Neighbor Embedding)에 대해 알아보겠습니다. LLE(지역적 선형 임베딩)와 SNE 모두 이웃이 되는 인스턴스를 기준으로 Embedding한다는 공통점을 가지고 있습니다. 하지만 이웃을 선택하는 방법에서 차이점이 있습니다. LLE는 이산적인 접근법으로 이웃을 확정하지만 SNE는 확률적인 방법으로 이웃을 정하게 됩니다. 좀 더 자세히 설명하면 LLE는 가장 가까운 $k$개의 인스턴스(k-Nearest Neighborhood)를 이웃으로 확정한 뒤에는 다른 인스턴스를 고려하지 않습니다. 하지만 SNE는 일정 범위 내의 인스턴스를 모두 고려하되 거리에 따라 확률을 부여하여 고려하게 됩니다. 가까운 인스턴스의 확률은 높고, 멀리 있는 인스턴스의 확률 낮게 반영하는 식으로요. 다시 말해, 확률적으로 지역성을 결정하겠다고 말할 수 있겠습니다.

고차원에서 특정 인스턴스 쌍을 이웃으로 선택할 확률을 $p$로 나타내고, 차원 축소를 하여 저차원에서 특정 인스턴스 쌍을 이웃으로 선택할 확률을 $q$로 나타내면 아래와 같습니다.

[\color{blue}{p_{i\vert j}} = \frac{\exp(-\frac{\Vert\color{blue}{\mathbf{x}i - \mathbf{x}_j}\Vert^2}{2\sigma^2_i})}{\sum{k\neq i}\exp(-\frac{\Vert\color{blue}{\mathbf{x}i - \mathbf{x}_k}\Vert^2}{2\sigma^2_i})} \qquad \color{red}{q{i\vert j}} = \frac{\exp(-{\Vert\color{red}{\mathbf{y}i - \mathbf{y}_j}\Vert^2})}{\sum{k\neq i}\exp({\Vert\color{red}{\mathbf{y}_i - \mathbf{y}_j}\Vert^2})}]

위 수식에서 $p$는 원 데이터의 차원에서 인스턴스 $i$가 인스턴스 $j$를 이웃으로 선택할 확률이며, $q$는 축소된 차원에서 인스턴스 $i$가 인스턴스 $j$를 이웃으로 선택할 확률입니다. $p,q$ 를 나타내는 수식은 비슷하게 생겼습니다. 우선 거리가 멀어질 수록 낮은 확률값을 할당하기 위해서 $y=e^{-x}$를 사용합니다. 이 함수에서는 $x$가 커질수록 함숫값이 작아지기 때문에 서로의 거리가 먼 인스턴스가 이웃으로 정해질 확률이 작아지게 됩니다. $y=e^{-x}$의 그래프는 아래와 같이 생겼습니다.

하지만 몇 가지 차이점도 가지고 있습니다. 먼저 $p$ 는 원래 인스턴스 좌표 $\mathbf{x}$ 에 대한 함수이며, $q$는 축소된 좌표계에서의 인스턴스의 좌표 $\mathbf{y}$에 대한 함수입니다. 그리고 $p$ 를 구하는 식에는 거리에 따른 확률값 차이를 얼마나 줄 것인지를 조정하는 $\sigma$ 가 있습니다. 이 값이 커지면 멀리 있는 인스턴스의 확률이 상대적으로 커지게 되고, 작게 하면 멀리 있는 인스턴스가 이웃으로 선택될 확률이 작아지게 됩니다. 실제로는 $\sigma$ 값이 $[5,50]$ 범위 중 어떤 값을 같더라도 t-SNE 자체가 실제로 강건(Robust)하게 작동하기 때문에 큰 고민없이 기본(Default)값으로 사용하는 것이 일반적입니다.

Cost function

우리의 목적은 두 확률 분포 $p,q$를 동일하게 만드는 것입니다. 따라서 이를 계산하기 위한 쿨백-라이블러 발산(Kullback-Leibler divergence, KLD)을 사용하여 두 값을 비교하게 됩니다. 쿨백-라이블러 발산은 비대칭(non-symmetric)이기 때문에 거리를 나타내는 수치는 아니지만 두 값의 엔트로피를 비교함으로써 목적함수로 사용됩니다. 수식으로 나타내면 아래와 같습니다.

[C = \sum_i KL(\color{blue}{P_i}\Vert \color{red}{Q_i}) = \sum_i\sum_j \color{blue}{p_{i\vert j}} \log \frac{\color{blue}{p_{i\vert j}}}{\color{red}{q_{i\vert j}}}]

두 확률 분포가 완전히 동일할 때 목적 함수의 값은 0이 되며 확률 분포가 달라질수록 목적 함수의 값은 커지게 됩니다.

Gradient Descent

이제 목적 함수가 최소인 지점을 찾기 위해서 경사 하강법을 사용하겠습니다. $\mathbf{x}$값은 이미 정해져 있고, 우리가 필요한 것은 위 값을 최소로 만드는 $\mathbf{y}$입니다. 그렇기 때문에 $\mathbf{y}$로 편미분한 그래디언트를 구합니다. 수식으로 나타내면 아래와 같습니다.

[\begin{aligned} C &= \sum_i\sum_j \color{blue}{p_{i\vert j}} \log \frac{\color{blue}{p_{i\vert j}}}{\color{red}{q_{i\vert j}}}
&= \sum_i\sum_j \color{blue}{p_{i\vert j}} \log \color{blue}{p_{i\vert j}} - \sum_i\sum_j \color{blue}{p_{i\vert j}} \log \color{red}{q_{i\vert j}}
C^\prime &= - \sum_i\sum_j \color{blue}{p_{i\vert j}} \log \color{red}{q_{i\vert j}}
&= -\sum_i \color{blue}{p_{t\vert i}} \log \color{red}{q_{t\vert i}} - \sum_j \color{blue}{p_{j\vert t}} \log \color{red}{q_{j\vert t}} - \sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}} \log \color{red}{q_{i\vert j}} \end{aligned}
\because \frac{\partial C}{\partial y_t} = \frac{\partial C^\prime}{\partial y_t}]

다음은 위 식의 각 항을 $\mathbf{y}$ 로 미분한 식을 구할 차례입니다. 식을 구하기 과정을 좀 더 간단하게 하기 위하여 계산 과정에서 나올 항을 다음과 같이 치환하도록 하겠습니다.

[d_{ti} = \exp(-\Vert \color{red}{\mathbf{y}t - \mathbf{y}_i}\Vert^2) = d{it}]

이를 활용하면 몇 가지 항을 아래와 같이 나타낼 수 있습니다.

[\frac{\partial d_{it}}{\partial \mathbf{y}t} = d^\prime{ti} = -2(\Vert\mathbf{y}t-\mathbf{y}_i\Vert) \exp(\Vert\mathbf{y}_t-\mathbf{y}_i\Vert^2) = -2(\mathbf{y}_t-\mathbf{y}_i)d{ti}
q_{t\vert i} = \frac{\exp(\Vert\mathbf{y}i-\mathbf{y}_t\Vert^2)}{\sum{k \neq i} \exp(\Vert\mathbf{y}i-\mathbf{y}_k\Vert^2)} = \frac{d{it}}{\sum_{k \neq i}d_{ik}}
q_{j\vert t} = \frac{\exp(\Vert\mathbf{y}t-\mathbf{y}_j\Vert^2)}{\sum{k \neq t} \exp(\Vert\mathbf{y}t-\mathbf{y}_k\Vert^2)} = \frac{d{tj}}{\sum_{k \neq i}d_{tk}}
q_{i\vert j} = \frac{\exp(\Vert\mathbf{y}j-\mathbf{y}_i\Vert^2)}{\sum{k \neq i} \exp(\Vert\mathbf{y}j-\mathbf{y}_k\Vert^2)} = \frac{d{ji}}{\sum_{k \neq j}d_{jk}}]

이제 이를 사용하여 본격적으로 각 항을 미분한 식을 구해보겠습니다. 첫 번째 항을 미분한 값은 아래와 같이 구해집니다.

[\begin{aligned} \frac{\partial}{\partial \mathbf{y}t}\bigg(-\sum_i \color{blue}{p{t\vert i}} \log \color{red}{q_{t\vert i}}\bigg) &= -\sum_i \color{blue}{p_{t\vert i}}\cdot \frac{1}{\color{red}{q_{t\vert i}}}\cdot \frac{\partial \color{red}{q_{t\vert i}}}{\partial y_t}
&= -\sum_i \color{blue}{p_{t\vert i}}\cdot \frac{1}{\color{red}{q_{t\vert i}}}\cdot \frac{d^\prime_{it}(\sum_{k \neq i}d_{ik}) - d_{it}d^\prime_{it}}{(\sum_{k \neq i}d_{ik})^2}
&= -\sum_i \color{blue}{p_{t\vert i}}\cdot \frac{1}{\color{red}{q_{t\vert i}}}\cdot \frac{-2(\mathbf{y}t-\mathbf{y}_i)d{ti}(\sum_{k \neq i}d_{ik}) +2(\mathbf{y}t-\mathbf{y}_i)d{ti}^2}{(\sum_{k \neq i}d_{ik})^2}
&= -\sum_i \color{blue}{p_{t\vert i}}\cdot \frac{1}{\color{red}{q_{t\vert i}}}\cdot \bigg(-2(\mathbf{y}t - \mathbf{y}_i) \cdot q{t\vert i} + 2(\mathbf{y}t - \mathbf{y}_i) \cdot q{t\vert i}^2\bigg)
&= \sum_i \color{blue}{p_{t\vert i}} \cdot 2(\mathbf{y}t - \mathbf{y}_i)(1 - q{t\vert i}) \end{aligned}]

두 번째 항을 미분한 값은 다음의 과정을 거쳐 구할 수 있습니다.

[\begin{aligned} \frac{\partial}{\partial \mathbf{y}t}\bigg(-\sum_j \color{blue}{p{j\vert t}} \log \color{red}{q_{j\vert t}}\bigg) &= -\sum_j \color{blue}{p_{j\vert t}}\cdot \frac{1}{\color{red}{q_{j\vert t}}}\cdot \frac{\partial \color{red}{q_{j\vert t}}}{\partial y_t}
&= -\sum_j \color{blue}{p_{j\vert t}}\cdot \frac{1}{\color{red}{q_{j\vert t}}}\cdot \frac{d^\prime_{tj}(\sum_{k \neq t}d_{tk}) - d_{tj}(\sum_{k \neq t}d^\prime_{tk})}{(\sum_{k \neq t}d_{tk})^2}
&= -\sum_j \color{blue}{p_{j\vert t}}\cdot \frac{1}{\color{red}{q_{j\vert t}}}\cdot \frac{-2(\mathbf{y}t-\mathbf{y}_j)d{tj}(\sum_{k \neq t}d_{tk}) - d_{tj}(\sum_{k \neq t}d^\prime_{tk})}{(\sum_{k \neq t}d_{tk})^2}
&= 2\sum_j \color{blue}{p_{j\vert t}} \cdot(\mathbf{y}t-\mathbf{y}_j) + \sum_j \color{blue}{p{j\vert t}} \cdot \frac{\sum_{k \neq t}d^\prime_{tk}}{\sum_{k \neq t}d_{tk}}
&= 2\sum_j \color{blue}{p_{j\vert t}} \cdot(\mathbf{y}t-\mathbf{y}_j) + \sum_j \frac{d^\prime{tj}}{\sum_{k \neq t}d_{tk}}
&= 2\sum_j \color{blue}{p_{j\vert t}} \cdot(\mathbf{y}t-\mathbf{y}_j) -2 \sum_j (\mathbf{y}_t-\mathbf{y}_j) \cdot \frac{d{tj}}{\sum_{k \neq t}d_{tk}}
&= 2\sum_j \color{blue}{p_{j\vert t}} \cdot(\mathbf{y}t-\mathbf{y}_j) -2 \sum_j (\mathbf{y}_t-\mathbf{y}_j) \cdot \color{red}{q{j\vert t}}
&= 2\sum_j (\mathbf{y}t-\mathbf{y}_j) \cdot (\color{blue}{p{j\vert t}} - \color{red}{q_{j\vert t}}) \end{aligned}]

마지막으로 세 번째 항을 미분한 값을 구해보겠습니다.

[\begin{aligned} \frac{\partial}{\partial \mathbf{y}t}\bigg(-\sum{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}} \log \color{red}{q_{o\vert j}}\bigg) &= -\sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}}\cdot \frac{1}{\color{red}{q_{i\vert j}}}\cdot \frac{\partial \color{red}{q_{i\vert j}}}{\partial y_t}
&= -\sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}}\cdot \frac{1}{\color{red}{q_{i\vert j}}}\cdot \frac{d^\prime_{ji}(\sum_{k \neq j}d_{jk}) - d_{ji}d^\prime_{jt}}{(\sum_{k \neq j}d_{ji})^2}
&= -\sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}}\cdot \frac{1}{\color{red}{q_{i\vert j}}}\cdot \frac{2(\mathbf{y}t-\mathbf{y}_i)d{ji}d_{jt}}{(\sum_{k \neq j}d_{jk})^2}
&= -\sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}}\cdot \frac{1}{\color{red}{q_{i\vert j}}}\cdot 2(\mathbf{y}t - \mathbf{y}_i) \cdot q{i\vert j}\cdot q_{t\vert j}
&= -\sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}} \cdot 2(\mathbf{y}t - \mathbf{y}_i) \cdot q{i\vert j} \end{aligned}]

첫 번째 항을 미분하여 나온 식과 세 번째 항을 미분하여 나온 식을 더한 후에 정리해보겠습니다.

[\begin{aligned} &\sum_i \color{blue}{p_{t\vert i}} \cdot 2(\mathbf{y}t - \mathbf{y}_i)(1 - q{t\vert i}) -\sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}} \cdot 2(\mathbf{y}t - \mathbf{y}_i) \cdot q{i\vert j}
=&\sum_j \color{blue}{p_{t\vert j}} \cdot 2(\mathbf{y}t - \mathbf{y}_j)(1 - q{t\vert j}) -\sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}} \cdot 2(\mathbf{y}t - \mathbf{y}_i) \cdot q{i\vert j}
=& 2\sum_j \color{blue}{p_{t\vert j}} \cdot (\mathbf{y}t - \mathbf{y}_j) - 2\sum_j \color{blue}{p{t\vert j}} \cdot (\mathbf{y}t - \mathbf{y}_j)q{t\vert j} -2\sum_{i \neq t}\sum_{j \neq t} \color{blue}{p_{i\vert j}} \cdot (\mathbf{y}t - \mathbf{y}_i) \cdot q{i\vert j}
=& 2\sum_j \color{blue}{p_{t\vert j}} \cdot (\mathbf{y}t - \mathbf{y}_j) - 2\sum_i\sum_j \color{blue}{p{t\vert j}} \cdot (\mathbf{y}t - \mathbf{y}_j)q{t\vert j}
=& 2\sum_j \color{blue}{p_{t\vert j}} \cdot (\mathbf{y}t - \mathbf{y}_j) - 2\sum_j (\mathbf{y}_t - \mathbf{y}_j)q{t\vert j}
=& 2\sum_j (\mathbf{y}t - \mathbf{y}_j) \cdot (\color{blue}{p{t\vert j}} - q_{t\vert j}) \end{aligned}]

이렇게 나온 식에 두 번째 항을 미분하여 나온 식을 더하여 식을 정리해보겠습니다.

[\begin{aligned} &2\sum_j (\mathbf{y}t - \mathbf{y}_j) \cdot (\color{blue}{p{t\vert j}} - q_{t\vert j}) + 2\sum_j (\mathbf{y}t-\mathbf{y}_j) \cdot (\color{blue}{p{j\vert t}} - \color{red}{q_{j\vert t}})
=& 2\sum_j (\mathbf{y}t - \mathbf{y}_j) \cdot (\color{blue}{p{t\vert j}} - q_{t\vert j} + \color{blue}{p_{j\vert t}} - \color{red}{q_{j\vert t}}) \end{aligned}]

이렇게 구해진 최종 식이 $\partial C/\partial \mathbf{y}_t$ 가 됩니다. 이 식을 사용하여 경사 하강법을 적용하여 최솟값이 되는 지점을 추적해나가는 것이 SNE의 값이 되겠습니다.

Symmetric SNE

조건부 확률을 pairwise한 확률로 바꾸어주기 위해서 다음과 같은 역할을 진행합니다. pairwise 확률은 다음과 같이 변하게 됩니다.

[p_{ij} = \frac{\exp(-\frac{\Vert\color{blue}{\mathbf{x}i - \mathbf{x}_j}\Vert^2}{2\sigma^2_i})}{\sum{k\neq l}\exp(-\frac{\Vert\color{blue}{\mathbf{x}k - \mathbf{x}_l}\Vert^2}{2\sigma^2_i})} \Rightarrow p{ij} = \frac{p_{j\vert i} + p_{i\vert j}}{2n} \quad \sum_j p_{ij} > \frac{1}{2n}]

이 확률을 적용한 SNE를 Symmetric SNE라고 하며, 쿨백-라이블러 발산을 사용한 목적 함수와 그래디언트는 다음과 같이 변하게 됩니다.

[C = \sum_i KL(\color{blue}{P_i}\Vert \color{red}{Q_i}) = \sum_i\sum_j \color{blue}{p_{ij}} \log \frac{\color{blue}{p_{ij}}}{\color{red}{q_{ij}}}
\because \frac{\partial C}{\partial y_i} = 4\sum_j (\mathbf{y}t - \mathbf{y}_j) \cdot (\color{blue}{p{ij}} - \color{red}{q_{ij}})]

t-SNE

위에서 구한 SNE에서는 Crowding problem이라는 문제가 발생합니다. SNE에서는 가우시안 분포(Gaussian distribution, 정규 분포)를 적용하여 인스턴스의 확률을 배정합니다. 가우시안 분포의 그래프를 보겠습니다.

이미지 출처 : wiki.analytica.com

위 그래프에서 빨간색으로 색칠된 부분, 즉 중심에서 가까운 부분보다 파란색으로 색칠된 부분에서 급격히 경사가 감소하는 것을 볼 수 있습니다. 이를 보정하기 위해서 t-SNE에서는 꼬리가 더 두꺼운 스튜던트 t-분포(Student’s t-distribution)를 사용합니다. 이 때 t-분포의 자유도는 1로 정합니다. t-분포의 식을 수식으로 나타내면 아래와 같습니다.

[f(t) = \frac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\nu\pi}\Gamma(\frac{\nu}{2})}(1+\frac{t^2}{\nu})^{-\frac{\nu+1}{2}}
\Gamma(n) = (n-1)!]

t-분포는 축소된 차원의 확률 분포인 $q$에만 적용되며 이때 $q$ 식은 아래와 같이 변하게 됩니다.

[\color{red}{q_{i\vert j}} = \frac{(1+{\Vert\color{red}{\mathbf{y}i - \mathbf{y}_j}\Vert^2})^{-1}}{\sum{k\neq l}(1+{\Vert\color{red}{\mathbf{y}_k - \mathbf{y}_l}\Vert^2})^{-1}}]

가우시안 분포에서 중심으로부터 떨어진 시점에서 감소. 그래서 t분포로 꼬리를 두껍게 해줌. 자유도 1인 t분포를 사용. p는 원래와 동일하게 가우시안을 쓰지만. q는 t분포를 사용한다.

3/4분기 회고

지난 번에 반기 회고를 적었는데 너무 오랜 기간에 대해 적으려니, (심지어 작년 것까지 적느라 8개월 적음) 시간이 너무 오래 걸리길래 분기마다 3개월치만 짧게 자주 적기로 하였습니다.

2020. Jul

7월에는 강필성 교수님의 텍스트 분석(Text Analytics)강의를 들으며 다양한 트랜스포머(Transformer) 기반 모델 및 자연어 태스크에 대한 공부를 했습니다. 이전에 프로젝트 진행할 때는 그저 KoGPT2를 붙여나 봐야겠다라는 생각뿐이었어서 이론적인 이해가 부족했었습니다. 이런 부분에 대해 채워갈 수 있는 시간이 되었습니다. 자료구조에 대한 공부도 이 때 조금 한 것 같고요. 코테 풀기에 재미 붙여서 1일 1문제 풀기도 했더랬습니다.

그리고 자소서도 한 두개 쓰고 그 중 한 기업이 서류를 잘 봐주셔서 면접도 준비했더랬습니다. 비록 결과는 잘 안되었지만… 더 공부를 많이 해야겠다고 생각하는 계기가 되었습니다. (떨어진 후에 읽기는 했지만 자연어 논문 풀로 읽은거 처음이야…)

2020. Aug

8월에는 예전에 블로그에 썼던 글을 리뉴얼 하였습니다. 예전에는 제가 공부한 내용에 대해서 낙서하는 형식으로 글을 썼지만, 지금은 그래도 설명하는 식으로 글을 작성하였습니다. 내용적으로도 틀린 부분이 있어서 수정하였고요. 아직도 잘못된 부분이 많아 복습할 때마다 고치려고 노력하고 있습니다.

이 때는 여러가지를 했네요. 일단 네이버에서 진행하는 부스트코스 코딩뉴비 챌린지 스터디 리더 역할도 했습니다. CS50 강의를 바탕으로 컴퓨터 사이언스 기초를 다지고 C언어를 조금이나마 다뤄보는 시간이 되엇습니다.

그리고 번역작업에도 컨트리뷰트 해보았습니다. MIT의 Missing semester의 Debugging and Profiling 번역하는 작업을 했는데 짧은 내용을 번역하는 것도 어찌나 어려운지… 만족스런 결과물은 아니지만 그래도 컨트리뷰트 해보았다는 것에 의의를 두고 싶습니다. 이것도 언제 시간을 내서 고치고 싶고 다른 부분도 번역해보고 싶네요.

2020. Sep

9월부터는 일을 시작해서 그쪽으로 집중하고 있습니다. 기획으로 입사하여 여러 잡다한 일을 하고 있습니다.

공부는 강필성 교수님의 비즈니스 분석(Business Analytics) 인강을 보고 있습니다. 원래 머신러닝을 배우며 많이 다루지 못하여 부족했던 부분이 차원축소, SVM, 부스팅 계열에 대한 지식이었습니다. 그런데 이번에 정확히 그쪽을 다루는 강의가 개설되어 인터넷으로 너무 잘 듣고 있습니다.

스터디는 2개를 신청했고 하나는 9월에 시작했네요. 먼저 한국인공지능연구소 AI 오픈랩을 신청하여 듣고 있습니다. 챗봇을 만드는 팀에 들어가게 되었습니다. 챗봇이 실제로 자연어처리에서 가장 많이 서비스되고 있는 분야중 하나인데 공부하면서 챗봇에 대해서 공부해본 적이 많이 없네요. 이번에 스터디를 통해 열심히 공부해보려고 합니다. (갑분 회고에서 다짐으로…)

나머지 하나는 풀잎스쿨 13기 수리통계학을 신청했습니다. 미약하지만 선대는 공부했는데 확률과 통계에 대한 부분이 너무 부족하더라고요. 이번에 열심히 공부해서 통계를 어느 정도는 정복하는 것으로…

해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

ISOMAP

이전에 알아본 주성분분석(PCA)과 다차원 척도법(MDS)은 알고리즘 내부 계산이 쉬울 뿐만 아니라 선형 구조를 가지는 데이터에 대해서 전역 최적점을 찾아낸다는 장점을 가지고 있습니다. 하지만 데이터가 비선형 구조를 가지고 있을 때에는 구조를 파악하지 못하여 두 방법을 사용하더라도 최적점을 찾아내지 못한다는 단점을 가지고 있습니다.

이번 시간에는 이런 문제를 해결할 수 있는, 즉 비선형 구조를 가진 데이터의 차원 축소를 위한 방법들에 대해서 알아보도록 하겠습니다. 첫 번째로 알아볼 방법은 ISOMAP(ISOmetric feature MAPping)입니다. ISOMAP은 다차원 척도법과 거의 유사하지만 인스턴스 사이의 거리(Distance)를 비선형 데이터 구조에 맞도록 계산해내는 단계에서 차이점을 가집니다.

특정 데이터셋의 구조가 아래 이미지와 같다고 해보겠습니다.

이미지 출처 : lovit.github.io

일반적인 다차원 척도법을 사용한다면 그림 A의 두 개 원이 가리키고 있는 두 인스턴스의 거리는 파란색 점선의 길이를 사용할 것입니다. 하지만 위와 같이 돌돌 말린(Swiss-roll) 데이터에서 두 점 사이의 실질적인 거리는 파란색 실선의 거리가 될 것입니다. 말려있는 데이터를 펼친 후에 두 인스턴스 사이의 거리인 것이지요.

위와 같이 데이터의 구조가 선형이 아니라 다양체(Manifold, 매니폴드)라면 각 인스턴스 사이의 거리를 다르게 정의해야 할 것입니다. ISOMAP은 이를 그래프(Graph) 구조로 해결하고자 하는 방법입니다. A에 있는 모든 인스턴스를 그래프 구조로 나타내면 B와 같이 변하게 됩니다. 그래프 구조에서는 최단 경로를 구하는 알고리즘이 이미 존재하므로 그래프 상에서 두 점 사이의 최단 경로를 구하여 실제 거리를 근사하게 됩니다. 그리고 이렇게 구해지는 각 인스턴스 사이의 거리가 ISOMAP에서의 거리가 됩니다.

Procedure

이제 ISOMAP이 어떤 과정을 통해 알고리즘을 수행하는지 알아보겠습니다. 인스턴스 사이의 거리를 구하는 것을 제외하고는 다차원 척도법과 동일한 계산과정을 거치기 때문에 간단한 편입니다.

첫 번째 단계는 각 인스턴스를 노드로 갖고 그 사이를 엣지로 연결하는 그래프 구조로 변형하는 것입니다. 연결하는 방법에 따라서 $\epsilon - \text{ISOMAP}$과 $k - \text{ISOMAP}$으로 나뉩니다. 전자는 일정한 기준 거리인 $\epsilon$을 설정한 후에 그보다 가까운 모든 인스턴스를 이웃 노드로 설정하여 연결합니다. 후자는 $k$개의 가장 가까운 인스턴스를 찾아 연결하는 방법입니다.

이렇게 모든 인스턴스를 연결했다면 두 번째 단계로 각 노드 사이의 최단 거리를 구하여 근접도(Proximity) 행렬을 만듭니다. 그래프 구조에서 노드 사이의 최단 경로를 구하는 알고리즘은 이미 알려져 있으므로 이 방법을 사용합니다.

마지막으로 이렇게 근접도 행렬을 구성한 이후에는 다차원 척도법에서 사용했던 방법을 사용하여 차원 축소를 수행할 수 있습니다.

Locally Linear Embedding

다음으로 알아볼 방법은 지역적 선형 임베딩(Locally Linear Embedding, LLE)입니다. 지역적 선형 임베딩은 고유벡터를 사용하는 방법으로 다루기가 쉽고 지역 최적점(Local optimum)에 빠지지 않을 수 있다는 장점을 가지고 있습니다. 비선형 임베딩 자체를 찾아내어 고차원 매니폴드 데이터를 저차원 데이터로 나타낼 수 있습니다. ISOMAP과 목적은 동일하지만 지역성(Locality)을 어떻게 수학적으로 반영하느냐에 따라서 지역적 선형 임베딩과 ISOMAP의 차이가 발생하게 됩니다.

Procedure

이어서 지역적 선형 임베딩이 수행하는 계산을 따라가 보겠습니다. 첫 번째 단계로 각 인스턴스의 이웃을 찾습니다. 다음 단계로는 각 인스턴스의 이웃으로부터 자기 자신을 재구축(reconstruct)할 수 있는 최적의 가중치 $W_{ij}$ 를 계산합니다. 수식으로 나타내면 아래의 목적 함수를 최소화하는 과정과 동일합니다.

[E(\mathbf{W}) = \sum_i \big\vert \mathbf{x}i - \mathbf{x}_i^\prime \big\vert^2 = \sum_i \big\vert \mathbf{x}_i - \sum_j\mathbf{W}{ij}\mathbf{x}_j\big\vert^2]

위 수식에서 $\mathbf{x}_i$ 는 재구축의 대상이 되는 원래의 인스턴스이며 그 뒤에오는 항은 이웃들과 가중치로부터 재구축한 $\mathbf{x}_i^\prime$ 입니다. 이 둘 사이의 차이를 줄이는 것이 목적이므로 평균 제곱 오차를 사용하여 나타낸 함수를 최소화하게 됩니다. 위 함수에서 가중치 값이 가지는 조건은 2가지 입니다. 첫 번째는 이웃이 아닌 인스턴스 $j$에 대해서는 가중치의 값이 0이라는 점이고, 두 번째는 모든 $i$마다 가중치의 합이 1이 된다는 점입니다. 수식으로는 아래와 같이 나타낼 수 있습니다.

[\sum_jW_{ij} = 1 \quad \forall_i]

이 최적화 문제를 모든 인스턴스 $i$에 대해서 풀어준 후에 나오는 가중치 행렬 $\mathbf{W}$는 지역성을 반영하는 행렬이 됩니다.

세 번째 단계로 이렇게 구한 가중치 $W$를 통해서 저차원에서 재구축한 인스턴스 $\mathbf{y}_i$를 최적화하는 문제를 풀게 됩니다. 수식으로 나타내면 아래와 같은 목적 함수를 최소화하는 과정이 됩니다.

[\Phi(\mathbf{W}) = \sum_i \big\vert \mathbf{y}i - \sum_j\mathbf{W}{ij}\mathbf{y}_j\big\vert^2]

이 세 단계를 그림으로는 아래와 같이 나타낼 수 있습니다.

이미지 출처 : lovit.github.io

먼저 이웃을 찾게 되고, 찾은 이웃들로부터 자기 자신을 가장 잘 재구축 할 수 있는 가중치를 구해냅니다. 가중치를 구한 이후에는 이를 사용하여 저차원 공간상에서 다시 재구축해냅니다.

세 번째 단계는 구체적으로 아래와 같이 풀어낼 수 있습니다. 수식으로 나타낸 세 번째 단계의 목표는 아래와 같습니다.

[\arg\min_y \Phi(\mathbf{W}) = \arg\min_y \sum_i \big\vert \mathbf{y}i - \sum_j\mathbf{W}{ij}\mathbf{y}_j\big\vert^2]

$\arg\min$이후의 식을 행렬을 사용하여 아래와 같이 나타낼 수 있습니다.

[\begin{aligned} \sum_i \big\vert \mathbf{y}i - \sum_j\mathbf{W}{ij}\mathbf{y}_j\big\vert^2 &= \bigg[(\mathbf{I} - \mathbf{W})\mathbf{y}\bigg]^T(\mathbf{I}-\mathbf{W})\mathbf{y}
&= \mathbf{y}^T (\mathbf{I} - \mathbf{W})^T (\mathbf{I} - \mathbf{W}) \mathbf{y}
&= \mathbf{y}^T\mathbf{M}\mathbf{y} \end{aligned}]

$(\mathbf{I} - \mathbf{W})$은 이미 알고있는 값이므로 $\mathbf{M}$역시 구할 수 있습니다. 이 때 $\mathbf{y}$가 단위 벡터(Unit vector)라면 $\mathbf{y}^T\mathbf{y} = 1$ 조건을 만족하므로 라그랑주 승수법을 통해 구할 수 있습니다. 이 과정은 주성분 분석에서 $\mathbf{w}^T\mathbf{S}\mathbf{w}$의 최댓값을 구했던 과정과도 동일합니다.

주성분분석은 $\mathbf{w}^T\mathbf{w} = 1$ 조건에서 $\mathbf{w}^T\mathbf{S}\mathbf{w}$ 식의 최댓값을 구하는 것이었으므로 고윳값(Eigenvalue)이 큰 순서대로 $d$개를 뽑아 사용하였습니다. 하지만 지역적 선형 임베딩은 $\mathbf{y}^T\mathbf{y} = 1$ 조건에서 $\mathbf{y}^T\mathbf{M}\mathbf{y}$ 의 최솟값을 구하는 것이므로 고윳값이 작은 순서대로 사용하게 됩니다. 이 때 가장 아래의 고유벡터는 버리기 때문에 $d$차원으로 줄이기 위해서는 고윳값이 작은 순서대로 $d+1$개의 고유벡터를 추출하면 됩니다.

해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

Multidimensional Scaling

다차원 척도법(Multidimensional Scaling, MDS)의 목적은 $d$ 차원 공간 상에 있는 객체의 거리를 최대한 보존하는 저차원의 좌표계를 찾는 것입니다. 주성분분석(Principal Component Analysis, PCA)와 다차원 척도법을 비교하면서 다차원 척도법에 대해서 알아보겠습니다.

Procedure

Step 1.

다차원 척도법을 수행하는 과정을 알아보겠습니다. 가장 첫 번째 스텝은 인스턴스 사이의 근접도(거리) 행렬을 만드는 것입니다. 객체의 좌표값이 존재한다면 근접도 행렬을 계산해낼 수 있습니다. 거리 행렬의 각 요소 $d_{ij}$는 다음과 같은 4개의 조건을 만족해야 합니다.

1. $d_{ij} \geq 0$
2. $d_{ii} = 0$
3. $d_{ij} = d_{ji}$
4. $d_{ij} \leq d_{ik} + d_{jk}$ (삼각부등식)

거리를 계산할 때에는 유클리드 거리(Euclidean)나 맨하탄 거리(Manhattan) 등을 사용하고, 유사도를 계산할 때에는 상관관계(Correlation)나 자카드 유사도(Jaccard)를 사용합니다. 주성분 분석에서 사용했던 $d \times n$ 크기의 Column-wise 행렬 $\mathbf{X}$로부터 $n \times n$ 크기의 근접도 행렬 $\mathbf{D}$를 계산한다면 아래의 식을 사용하여 각 요소의 값을 구할 수 있습니다.

[d_{rs}^2 = (\mathbf{x}_r-\mathbf{x}_s)^T(\mathbf{x}_r-\mathbf{x}_s)]

Step 2.

두 번째로 해야 하는 일은 거리 정보를 최대한 보존하는 좌표 시스템을 찾는 것입니다. 다차원 축소법의 주된 알고리즘이 개입되는 부분이기도 합니다. 근접도 행렬 $\mathbf{D}$로부터 이들의 거리를 최대한 보존하는 $d$ 차원의 좌표계 $\mathbf{X}$를 바로 찾는 것은 어렵습니다. 그렇기 때문에 각 인스턴스의 내적값을 요소로 갖는 $\mathbf{B}$라는 행렬을 매개체로써 한 번 거쳐가도록 합니다. 간단하게 나타내면 아래와 같습니다.

[\mathbf{D} \text{ (Proximity matrix)} \Rightarrow \mathbf{B} \text{ (Inner product matrix)} \Rightarrow \mathbf{X} \text{ (Coordinate matrix)}
b_{rs} = \mathbf{x}_r^T\mathbf{x}_s]

이제 $\mathbf{D}$로부터 $\mathbf{B}$를 만들겠습니다. 실질적인 계산을 하기 전에 가정해야 할 사항이 있습니다. 모든 변수의 평균이 $0$이 된다는 점입니다. 따라서, 아래의 식이 성립하게 됩니다.

[\sum_{r=1}^n x_{ri} = 0, (i=1,2, \cdots, p)]

이제 준비도 마쳤으니 $\mathbf{B}$의 요소인 $\mathbf{x}_r^T\mathbf{x}_s$를 본격적으로 찾아보도록 하겠습니다. 먼저 위에서 알아본 거리 행렬 요소에 관한 식을 전개해보겠습니다.

[\begin{aligned} d^2_{rs} &= (\mathbf{x}_r-\mathbf{x}_s)^T(\mathbf{x}_r-\mathbf{x}_s)\ &= \mathbf{x}_r^T\mathbf{x}_r + \mathbf{x}_s^T\mathbf{x}_s - 2\mathbf{x}_r^T\mathbf{x}_s \end{aligned}]

우리의 목적은 우변의 마지막 항인 $\mathbf{x}_r^T\mathbf{x}_s$을 구하는 것이므로 나머지 항을 하나의 문자로 치환하기 위해서 수학적 트릭을 사용하겠습니다. 트릭의 첫 번째 과정으로 각 문자 $r,s$에 대해서 각 항의 평균값을 구해보겠습니다. 먼저 $r$에 대한 평균을 구할 때의 수식은 아래와 같이 변하게 됩니다.

[\frac{1}{n}\sum^n_{r=1} d^2{rs} = \frac{1}{n}\sum^n{r=1}\mathbf{x}r^T\mathbf{x}_r + \frac{1}{n}\sum^n{r=1}\mathbf{x}s^T\mathbf{x}_s - \frac{2}{n}\sum^n{r=1}\mathbf{x}r^T\mathbf{x}_s = \frac{1}{n}\sum^n{r=1}\mathbf{x}r^T\mathbf{x}_r + \mathbf{x}_s^T\mathbf{x}_s
\color{blue}{\therefore \mathbf{x}_s^T\mathbf{x}_s = \frac{1}{n}\sum^n{r=1} d^2{rs} - \frac{1}{n}\sum^n{r=1}\mathbf{x}_r^T\mathbf{x}_r}]

마찬가지로 $s$에 대한 평균을 구할 때의 수식은 아래와 같이 변하게 됩니다.

[\frac{1}{n}\sum^n_{s=1} d^2{rs} = \frac{1}{n}\sum^n{s=1}\mathbf{x}r^T\mathbf{x}_r + \frac{1}{n}\sum^n{s=1}\mathbf{x}s^T\mathbf{x}_s - \frac{2}{n}\sum^n{s=1}\mathbf{x}r^T\mathbf{x}_s = \mathbf{x}_r^T\mathbf{x}_r + \frac{1}{n}\sum^n{s=1}\mathbf{x}s^T\mathbf{x}_s
\color{red}{\therefore \mathbf{x}_r^T\mathbf{x}_r = \frac{1}{n}\sum^n{s=1} d^2{rs} - \frac{1}{n}\sum^n{s=1}\mathbf{x}_s^T\mathbf{x}_s}]

트릭을 통해서 두 항 $\mathbf{x}_s^T\mathbf{x}_s, \mathbf{x}_r^T\mathbf{x}_r$ 은 치환할 수 있게 되었지만 치환 과정에서 다른 항들이 나오게 됩니다. 이 항을 처리하기 위해서 또 다른 트릭을 한 번 더 사용합니다.

[\begin{aligned} \frac{1}{n^2}\sum^n_{r=1}\sum^n_{s=1} d^2{rs} &= \frac{1}{n^2}\sum^n{r=1}\sum^n_{s=1}\mathbf{x}r^T\mathbf{x}_r + \frac{1}{n^2}\sum^n{r=1}\sum^n_{s=1}\mathbf{x}s^T\mathbf{x}_s - \frac{2}{n^2}\sum^n{r=1}\sum^n_{s=1}\mathbf{x}r^T\mathbf{x}_s
&= \frac{1}{n}\sum^n{r=1}\mathbf{x}_r^T\mathbf{x}_r

• \frac{1}{n}\sum^n_{s=1}\mathbf{x}s^T\mathbf{x}_s = \frac{2}{n}\sum^n{r=1}\mathbf{x}r^T\mathbf{x}_r \end{aligned}
  \color{olive}{\therefore \frac{2}{n}\sum^n{r=1}\mathbf{x}r^T\mathbf{x}_r = \frac{1}{n^2}\sum^n{r=1}\sum^n_{s=1} d^2_{rs}}]

이제 모든 항을 처리할 수 있게 되었습니다. 이제 처음에 $d^2_{rs}$에 대해서 나타냈던 식을 활용하여 $b$ 를 나타내보도록 하겠습니다.

[\begin{aligned} b_{rs} &= \mathbf{x}r^T\mathbf{x}_s
&= - \frac{1}{2}(d^2{rs}-\mathbf{x}r^T\mathbf{x}_r - \mathbf{x}_s^T\mathbf{x}_s) \qquad \because d^2{rs} = \mathbf{x}r^T\mathbf{x}_r + \mathbf{x}_s^T\mathbf{x}_s - 2\mathbf{x}_r^T\mathbf{x}_s
&= - \frac{1}{2}(d^2{rs} - \frac{1}{n}\sum^n_{s=1} d^2{rs} + \frac{1}{n}\sum^n{s=1}\mathbf{x}s^T\mathbf{x}_s - \frac{1}{n}\sum^n{r=1} d^2{rs} + \frac{1}{n}\sum^n{r=1}\mathbf{x}r^T\mathbf{x}_r)
&= - \frac{1}{2}(d^2{rs} - \frac{1}{n}\sum^n_{s=1} d^2{rs} - \frac{1}{n}\sum^n{r=1} d^2{rs} + \frac{1}{n^2}\sum^n{r=1}\sum^n_{s=1} d^2_{rs}) \end{aligned} \]

마지막 식을 다른 형태로 치환하여 나타낼 수 있습니다.

[\begin{aligned} b_{rs} &= - \frac{1}{2}(d^2{rs} - \frac{1}{n}\sum^n{s=1} d^2{rs} - \frac{1}{n}\sum^n{r=1} d^2{rs} + \frac{1}{n^2}\sum^n{r=1}\sum^n_{s=1} d^2{rs})
&= a{rs} - a_{r\cdot} - a_{\cdot s} + a_{\cdot\cdot} \end{aligned}]

$a_{rs}$ 를 행렬 $\mathbf{A}$의 성분이라 하면 우리가 구하려던 행렬 $\mathbf{B}$는 아래와 같이 구할 수 있습니다.

[\mathbf{B} = \mathbf{HAH} \qquad \mathbf{H} = \mathbf{I} - \frac{1}{n}\mathbf{11}^T]

이렇게 구한 행렬 $\mathbf{B}$는 아래와 같이 나타낼 수 있습니다.

[\mathbf{B} = \mathbf{XX}^T]

행렬 $\mathbf{B}$는 대칭행렬이며 양의 준정부호 행렬(Positive semi-definite matrix)이기 때문에 행렬 $\mathbf{X}$ 의 랭크가 $p$ 라면 $\mathbf{B}$ 는 $p$ 개의 양수인 고윳값과 $n-p$ 개의 $0$인 고윳값을 가지고 있습니다. 따라서 고윳값 분해(Eigenvalue factorization)를 통해서 아래와 같이 분해할 수 있습니다.

[\mathbf{B}_1 = \mathbf{V}_1\mathbf{\Lambda}_1\mathbf{V}_1^T
\mathbf{\Lambda}_1 = \text{diag}(\lambda_1, \lambda_2, \cdots ,\lambda_p)]

고윳값 분해로 만들어 낸 식을 아래와 같이 나타낼 수 있으므로 우리가 구하고자 하는 좌표 행렬 $\mathbf{X}$를 구할 수 있게 됩니다.

[\mathbf{B}_1 = \mathbf{V}_1\mathbf{\Lambda}_1\mathbf{V}_1^T = (\mathbf{V}_1\mathbf{\Lambda}_1^{1/2})(\mathbf{V}_1\mathbf{\Lambda}_1^{1/2})^T
\therefore \mathbf{X} = \mathbf{V}_1\mathbf{\Lambda}_1^{1/2}]

해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

Principal Component Analysis

차원 축소의 목적은 주어진 태스크를 수행하는 모델을 만들기 위해서 원래의 데이터가 가진 정보를 최대한 보존하면서도 더욱 차원이 적은 데이터셋을 구성하는 것이었습니다. 이전 시간까지 알아본 전진 선택, 후진 제거, Stepwise, 유전 알고리즘 등은 특성 선택(Feature selection)을 위한 알고리즘이었습니다. 특성 선택은 원래 존재하는 특성 중에서 더 중요한 특성의 부분 집합만을 선택하는 방법입니다.

반대로 오늘 알아볼 주성분 분석, 다음 시간에 등장할 다차원 척도법 등은 특성 추출(Feature extraction)을 위한 알고리즘입니다. 특성 추출은 데이터가 가지고 있는 특성을 모두 보존하는 방향으로, 각 특성들을 결합하여 새로운 특성을 생성하는 방법입니다. 이 중 주성분 분석(Principal Component Analysis, PCA)은 원래 데이터를 사영시켰을 때 원래 데이터의 분산을 최대한 보존하는 기저 벡터를 찾는 방법입니다. 주성분분석을 이미지로 살펴보도록 하겠습니다.

이미지 출처 : stackexchange.com

위의 원래 데이터는 2차원 평면상에 펼쳐져 있습니다. 만약 이 데이터를 1차원인 직선상에 나타낸다면 어떤 직선을 선택하는 것이 가장 좋을 지를 알아내는 방법이 바로 주성분분석입니다. 위 그림에서는 분홍색 선과 이어지는 직선으로 결정되는 것을 볼 수 있습니다. 만약 다른 축을 선택했다면 어떻게 되었을까요? 아래 그림은 다양한 방향의 직선에 대해서 사영되는 데이터의 모습을 보여주고 있습니다.

이미지 출처 : stackexchange.com

위 이미지에 등장하는 직선과 그에 사영되는 점을 보겠습니다. 위와 같이 분홍색과 이어지는 직선에서는 데이터가 퍼진 형태를 잘 보존하고 있는 것을 알 수 있습니다. 반대로 그와 직교하는 직선의 방향이 에서는 모든 점이 가운데로 모여 데이터가 퍼져있는 모습을 잘 나타내지 못하는 것을 볼 수 있습니다. 이러한 축을 주성분 이라고 하며 주성분에 데이터를 사영하는 것이 주성분 분석의 목적입니다.

Background Knowledge

주성분분석에 사용되는 수리적 배경에 대해서 알아보겠습니다. 첫 번째는 공분산 행렬(Covariance matrix) $\text{Cov}$ 입니다. $\text{Cov}$ 는 $n \times n$ 사이즈의 행렬입니다. 수식으로는 다음과 같이 정리됩니다.

[\text{Cov}(\mathbf{X}) = \frac{1}{n}(\mathbf{X} - \bar{\mathbf{X}})(\mathbf{X} - \bar{\mathbf{X}})^T]

위 식에서 $\mathbf{X}_{d \times n}$ 는 데이터셋을 Column-wise vector의 행렬로 나타낸 것입니다. 일반적으로 데이터셋을 행렬로 나타낼 때에는 인스턴스(Instance)를 각 행(Row)에, 특성을 각 열(Column)에 배치하는 Row-wise vector 방식으로 표현합니다. $d$ 는 특성의 개수이며 $n$ 은 데이터의 개수입니다. 하지만 공분산 행렬을 구할 때에는 이를 전치하여 나타낸 Column-wise vector 방식의 표현을 사용합니다. 이렇게 구해진 공분산 행렬의 사이즈는 $n \times n$ 이며 대칭 행렬(Symmetric matrix)입니다. 이렇게 구해진 공분산 행렬의 대각 성분(Diagonal term)을 모두 더한 Trace를 구하면 원래 데이터셋의 분산을 구할 수 있습니다.

다음으로 알아야 하는 개념은 사영(Projection)입니다. 아래 그림은 특정 벡터 $\vec{a}$를 다른 벡터 $\vec{b}$ 에 사영했을 때의 벡터를 $\vec{a_1}$ 으로 나타낸 그림입니다.

이미지 출처 : wikipedia.org/wiki/Vector_projection

이 때 사영의 과정을 미지수 $p$로 나타내면 $\vec{a_1} = p\vec{b}$ 라고 나타낼 수 있고 $\vec{a_2} = \vec{a} - p\vec{b}$로 나타낼 수 있으므로 다음과 같은 식이 성립하게 됩니다.

[\begin{aligned} \vec{a_2}^T\vec{b} = (\vec{a} - p\vec{b})^T\vec{b} &= 0
\vec{a}^T\vec{b} - p\vec{b}^T\vec{b} &= 0
\end{aligned}
\begin{aligned} &\therefore p = \frac{\vec{a}^T\vec{b}}{\vec{b}^T\vec{b}}
&\because \vec{a_2} \perp \vec{b} \end{aligned}]

구해낸 $p$를 사용하여 $\vec{a_1}$을 표현할 수 있습니다.

[\vec{a_1} = p\vec{b} = \frac{\vec{a}^T\vec{b}}{\vec{b}^T\vec{b}}\vec{b}]

만약 $\vec{b}$ 가 단위 벡터(unit vector)라면 $\Vert\vec{b}\Vert = 1$ 이므로 다음과 같은 식이 성립하게 됩니다.

[\vec{a_1} = p\vec{b} = (\vec{a}^T\vec{b})\vec{b}
\because \vec{b}^T\vec{b} = \Vert\vec{b}\Vert^2 = 1]

마지막으로 알아야 할 개념은 고윳값(eigenvalue)과 고유벡터(eigenvector)입니다. 행렬 $A$를 사용하여 모든 벡터를 선형 변환(Linear transformation)하면 방향이 바뀌는 벡터가 있고 그렇지 않은 벡터가 있습니다. 아래 그림을 보겠습니다.

이미지 출처 : commons.wikimedia.org

위 그림에서 빨간색으로 나타나는 벡터는 선형 변환에 의해서 방향이 바뀝니다. 반대로 파란색으로 나타나는 벡터는 크기는 변할지언정 방향은 변하지 않고, 핑크색으로 나타나는 벡터는 크기도 방향도 변하지 않는 것을 볼 수 있습니다. 이들처럼 방향이 변하지 않는 벡터를 고유벡터(Eigenvector)라고 하며 파란색 벡터처럼 고유벡터의 크기가 원래의 벡터보다 $k$ 배 변할 때 이 값 $k$를 해당 고유벡터의 고윳값(Eigenvalue)라고 합니다.

How to find PC

위 지식을 사용하여 주성분을 어떻게 찾는 지에 대해서 알아보겠습니다. 첫 번째 과정으로 데이터셋의 평균이 0이 되도록 변환(Centering)합니다. 위에서 공분산 행렬을 구했던 과정과도 비슷합니다. $\mathbf{X} - \bar{\mathbf{X}}$ 를 해주어 모든 데이터셋의 평균을 0으로 만들어줍니다. 지금부터는 이렇게 변환된 행렬을 다시 $\mathbf{X}$라고 나타내겠습니다.

우리의 목표는 차원을 축소한 행렬의 분산을 구하는 것입니다. 따라서 변환한 행렬 $\mathbf{X}$를 특정 기저 벡터 $\mathbf{w}$ 에 사영한 행렬의 공분산 행렬을 구합니다. 식은 위에서 구했던 것과 동일하므로 아래와 같이 나타낼 수 있습니다. 아래 식에서 $\mathbf{S}$는 변환된 행렬 $\mathbf{X}$ 의 표본 공분산 행렬(Sample covariance matrix)입니다.

[V = \frac{1}{n}(\mathbf{w}^T\mathbf{X})(\mathbf{w}^T\mathbf{X})^T = \frac{1}{n}\mathbf{w}^T\mathbf{X}\mathbf{X}^T\mathbf{w} = \mathbf{w}^T\mathbf{S}\mathbf{w}]

우리의 목표는 $V$를 최대화 하는 지점, 즉 $\max \mathbf{w}^T\mathbf{S}\mathbf{w}$ 를 찾는 것이므로 라그랑주 승수법(Lagrangian multiplier)을 사용하여 아래와 같이 구할 수 있습니다.

[\max \mathbf{w}^T\mathbf{S}\mathbf{w} \qquad s.t. \mathbf{w}^T\mathbf{w} = 1
L = \mathbf{w}^T\mathbf{S}\mathbf{w} - \lambda(\mathbf{w}^T\mathbf{w} - 1)
\frac{\part L}{\part \mathbf{w}} = 0 \Rightarrow \mathbf{S}\mathbf{w} - \lambda\mathbf{w} = (\mathbf{S} - \lambda\mathbf{I})\mathbf{w} = 0]

예를 들어, 2차원 데이터에 대하여 $\mathbf{S}, \lambda$ 가 각각 아래와 같이 나왔다고 해보겠습니다.

[\mathbf{S} = \left[\begin{array}{cc} 0.6779 & -0.7352 \ 0.7352 & 0.6779 \end{array} \right] \qquad \lambda = \left[\begin{array}{cc} 1.2840 & 0.0491 \end{array} \right]]

이중 $\lambda_1 = 1.2840, \lambda_2 = 0.0491$ 이라 하면 $e_1 = \left[\begin{array}{cc} 0.6779 & 0.7352 \end{array} \right]^T$ 를 주성분으로 선택했을 때 보존되는 분산의 비율을 아래와 같이 구할 수 있습니다.

[\frac{\lambda_1}{\lambda_1+\lambda_2} = \frac{1.2840}{1.2840 + 0.0491} \approx 0.96]

위와 같이 2차원 데이터를 1차원으로 축소하더라도 원래 데이터 분산의 96% 정도를 보존하는 것을 알 수 있습니다.

Issues

다음으로 주성분 분석을 수행할 때 고려해야 할 몇 가지 이슈에 대해서 알아보겠습니다. 몇 개의 차원으로 축소할 것인가, 즉 몇 개의 변수를 택할 것인가에 대한 문제입니다. 사실 이 문제에 대한 명시적인 해는 없습니다. 해를 찾기 위한 방법으로는 정성적인 방법과 정량적인 방법이 있습니다. 먼저 해당 도메인 지식이 풍부한 전문가가 판단하는 정성적 방법이 있습니다.

정량적인 방법은 2가지로 나뉩니다. 첫 번째는 엘보우 지점(Elbow point)을 찾는 것입니다. 이 지점은 아래의 $n$개의 주성분을 선택할 때 $n$번째의 주성분이 보존하는 분산의 비율을 나타낸 것입니다. 아래 그림에서 첫 번째 주성분은 원래 데이터 분산의 약 10%를 보존하고 있으며, 점점 주성분이 추가될 때마다 그 주성분에 의해 추가되는 분산의 비율은 줄어드는 것을 볼 수 있습니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

위 그림에서 빨간색 표시가 되어있는 지점, 즉 하나의 주성분을 더 추가하더라도 분산을 많이 보존하지 못하는 지점을 엘보우 지점이라고 하며 엘보우 지점의 바로 앞 단계 만큼의 주성분을 보존하는 것이 하나의 방법입니다. 두 번째 방법은 보존 하고자 하는 분산 비율의 기준점을 정하고 그 기준을 넘기는 지점까지의 주성분을 선택하는 방법입니다. 위에서 보았던 그림을 누적 그래프로 나타낸 그림입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

위 그림에서는 원래 데이터 분산의 80%를 기준점으로 사용하였고 그 이상의 분산을 보존하는 지점까지만 주성분을 선택합니다.

다음 이슈는 주성분 분석에서 고려해야 할 점입니다. 주성분 분석은 대상이 되는 데이터가 가우시안 분포(Gaussian distribution)를 이루고 있음을 가정하고 있습니다. 그렇기 때문에 가우시안 분포를 가지지 않는 데이터에 주성분 분석을 사용한다면 결과물이 유효하다고 할 수 없습니다.

마지막 이슈는 주성분 분석이 데이터의 결정 경계를 찾기 위해 사용하는 방법은 아니라는 점입니다. 아래 그림은 특정 데이터셋에 대하여 주성분 분석을 사용했을 때 찾아지는 기저와 분류를 위한 방법인 FLDA(Fisher’s Linear Discriminant Analysis)를 사용했을 때 찾아지는 축을 나타낸 것입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

위 그림의 데이터를 더 잘 분류할 수 있는 방법은 FLDA입니다. PCA는 분산을 최대화 하는 기저를 찾는 것 뿐이므로 결정 경계를 찾는 데에 적절한 방법론은 아님을 알 수 있습니다.