CNN

합성곱 신경망(Convolutional Neural Network, CNN)은 컴퓨터 비전(Computer vision)분야에서 특히 많이 쓰이는 신경망입니다. 합성곱 신경망이 주목을 받게 된 것도 2012년 이미지넷(ImageNet) 데이터셋을 분류하는 ILSVRC대회에서 우승한 AlexNet 덕분이었습니다.

이미지 분류에서 합성곱 신경망이 주목받게 된 이유는 무엇일까요? 이미지는 위치에 맞는 공간적인 특성을 가지고 있습니다. 하지만 일반적인 완전 연결층(Fully connected layer)은 모든 입력 값을 동등하게 취급하기 때문에 이런 공간적 특성을 잘 살려내지 못합니다. MNIST 손글씨 데이터를 완전 연결층으로 분류해본 분이라면 $(24,24)$ 데이터를 $(768,)$ 로 펼친 뒤에 신경망에 넣어본 적이 있을 것입니다. 물론 손글씨 데이터는 색상도 흑백인데다가 패턴이 간단하기 때문에 완전 연결 층으로도 꽤 좋은 분류기를 구현할 수 있습니다. 하지만 패턴이 복잡한 컬러 이미지를 이런 방식으로 분류하는 것은 쉬운일이 아닙니다.

반면 합성곱 신경망은 학습 과정에서 이런 공간적 특성을 보존하며 학습할 수 있습니다. 합성곱 층은 완전 연결 층과 달리 3차원 데이터를 입력받아 다시 3차원 데이터를 내놓습니다. 덕분에 층이 깊어지더라도 공간적 특성을 최대한 보존하며 학습할 수 있습니다.

Structure

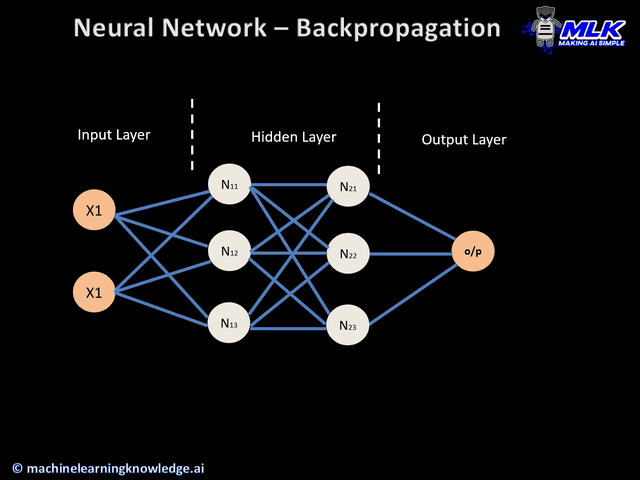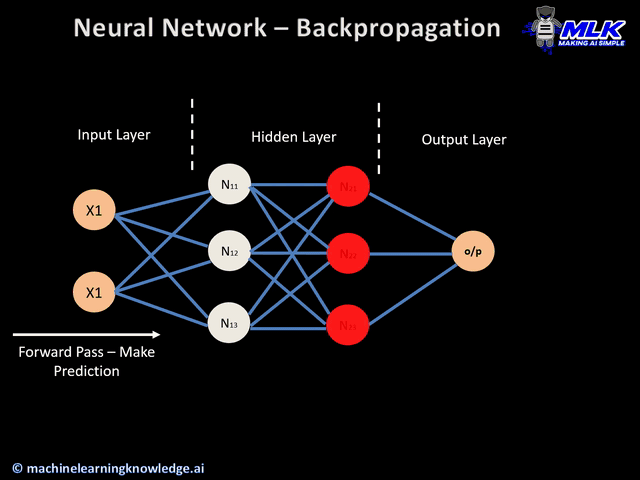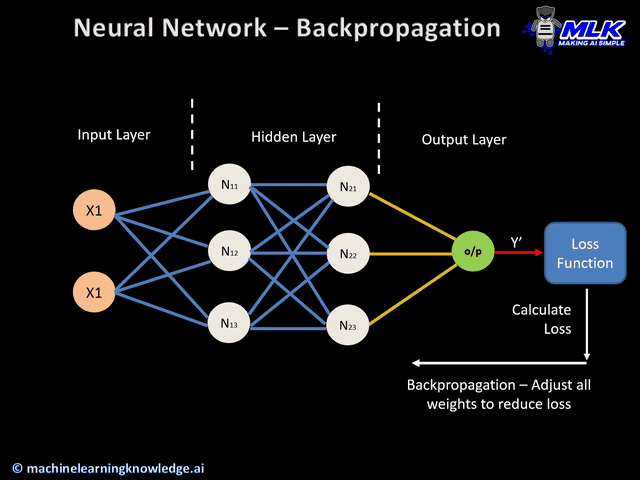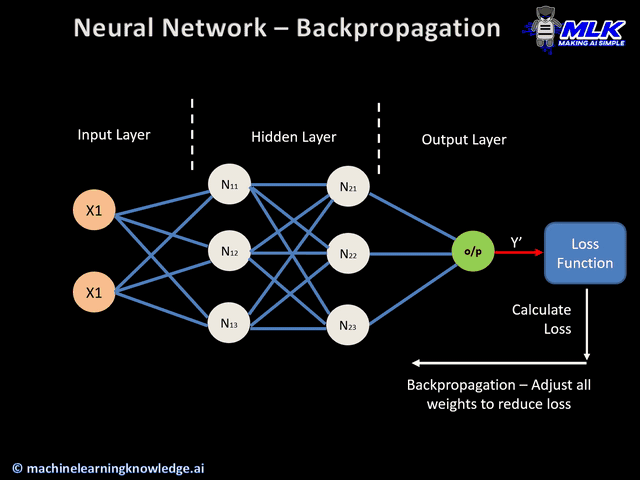
합성곱 신경망의 구조가 어떻기에 이런 공간적 특성을 보존할 수 있는 것일까요? 먼저 합성곱 신경망의 구조를 살펴보겠습니다.

이미지 출처 : medium.com/@sdoshi579

합성곱 신경망은 크게 두 종류의 층으로 이루어져 있습니다. 하나는 위 그림에서 하늘색에 해당하는 합성곱 층(Convolutional layer)이고 나머지 하나는 주황색에 해당하는 풀링 층(Pooling layer)입니다. 마지막에는 분류를 위해 완전 연결 층을 하나 결합하여 사용합니다. 각 층에서 어떤 일이 일어나는지 하나씩 알아보도록 하겠습니다.

Conv Layer

합성곱 층은 입력 데이터에 특정 크기의 커널(Kernal matrix)을 적용하여 새로운 출력값을 계산하는 역할을 합니다. 아래 그림은 합성곱 층에서 입력 데이터로부터 합성곱 연산을 수행하는 과정을 나타낸 것입니다.

이미지 출처 : stackoverflow.com

커널은 왼쪽 위부터 시작하며 오른쪽 끝까지 행렬 원소끼리의 곱을 수행한 후에 다시 아래쪽 열 왼쪽부터 오른쪽으로 동일한 과정을 수행합니다. 커널에 있는 $0, -1, 5$와 같은 숫자는 파라미터이며 학습을 통해서 갱신됩니다. 합성곱 신경망에는 커널 외에도 편향을 적용할 수 있습니다. 커널과의 합성곱을 통해 나온 행렬의 모든 원소에 편향을 더하여 적용합니다. 합성곱 층에는 커널의 크기 외에도 옵션으로 적용할 수 있는 패딩과 스트라이드가 있습니다. 먼저 패딩의 역할부터 알아보겠습니다.

패딩(Padding)은 위 예시에서 볼 수 있는 것처럼 입력 데이터 주변을 특정 값으로 채우는 것을 패딩이라고 합니다. 위 예시에서는 값이 0이고 폭이 1인 패딩이 적용되었습니다. $1 \times 1$ 보다 큰 크기의 커널을 사용하면 합성곱 연산의 특성상 입-출력 크기가 많이 달라집니다. 패딩은 이런 크기 변화를 완화해주는 역할을 합니다. 위 예시에서도 폭이 1인 패딩을 사용하지 않았다면 출력되는 행렬의 크기는 $5 \times 5$ 가 아니라 $3 \times 3$ 으로 줄어들 것입니다. 패딩은 행렬 바깥에 특정한 값을 둘러줌으로써 이미지 가장자리 부분의 특성을 보존할 수 있다는 장점이 있습니다.

스트라이드(Stride)는 필터를 적용하는 위치의 간격입니다. 위에서 살펴본 예시에서는 스트라이드가 $1$로 오른쪽으로 $1$칸씩 이동하면서 합성곱을 수행한 뒤에 $1$칸 아래로 이동하여 같은 과정을 반복합니다. 스트라이드가 $2$이면 오른쪽으로 $2$칸씩 이동하면서 합성곱을 수행하고 오른쪽 끝에 닿으면 $2$칸 아래로 이동하여 같은 과정을 반복하게 됩니다.

패딩은 합성곱의 대상이 되는 행렬을 확장해주는 반면, 스트라이드는 일정 간격으로 합성곱을 건너뜁니다. 이 때문에 패딩을 늘리면 출력 크기가 늘어나게 되고, 스트라이드를 늘리면 출력 크기는 줄어들게 됩니다. 입력 데이터의 높이와 너비를 각각 $H, W$라 하고 커널의 높이와 너비를 $KH, KW$ 그리고 패딩과 스트라이드를 각각 $P, S$ 라 하면 출력 데이터의 크기는 아래와 같은 수식을 통해 구할 수 있습니다.

[OH = \frac{H+2P-FH}{S}+1 \qquad OW = \frac{W+2P-FW}{S}+1]

위 예시에서 입력 데이터의 사이즈는 $5 \times 5$ 이며 커널의 크기는 $3 \times 3$ 이었습니다. 패딩은 $1$이 적용되었고 스트라이드도 $1$이므로 아래 수식을 통해서 출력 데이터의 크기를 구할 수 있습니다.

[OH = \frac{5+2\cdot 1-3}{1}+1=5 \qquad OW = \frac{4+2\cdot 1-3}{1}+1=5]

위 수식으로 출력데이터의 크기 $5 \times 5$를 정확히 구해낼 수 있습니다.

with Channels

컬러 이미지인 경우에는 이미지의 차원이 더 늘어납니다. RGB값을 각각 적용하기 때문입니다. 이렇게 채널이 많아지는 경우에는 채널 갯수만큼의 커널을 각각 적용하여 병렬 연산을 한 뒤에 그 합을 출력데이터에 입력합니다. 아래의 그림은 3개의 채널로 구성된 입력 데이터의 합성곱 연산이 수행되는 과정을 이미지로 나타낸 것입니다.

이미지 출처 : thelearningmachine.ai

Pooling Layer

풀링 층에서는 가로, 세로 방향의 공간을 줄이기 위한 풀링(Pooling)을 수행합니다. 풀링 방법에는 최대 풀링(Max pooling)과 평균 풀링(Average pooling)이 있습니다. 최대 풀링은 정해진 범위 내에서 가장 큰 값을 꺼내오는 방식이며 평균 풀링은 정해진 범위 내에 있는 모든 요소의 평균을 가져오는 방식입니다. 일반적으로 이미지를 처리할 때에는 각 부분의 특징을 최대로 보존하기 위해서 최대 풀링을 사용하고 있습니다. 아래 그림은 $2 \times 2$ 크기의 최대 풀링과 평균 풀링을 처리하는 과정을 비교하여 나타낸 것입니다.

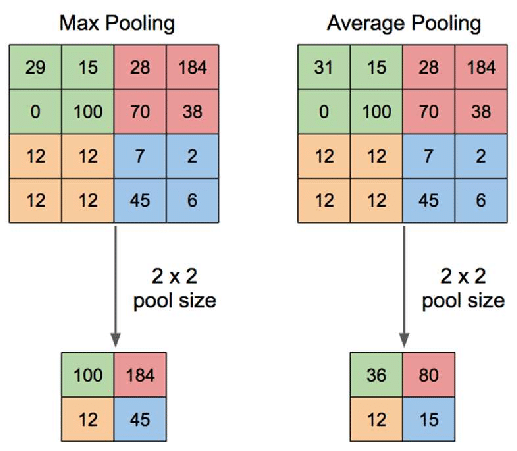
이미지 출처 : quora.com

위 그림에서 왼쪽은 최대 풀링으로 각각의 $2 \times 2$의 범위 내에서 가장 큰 요소인 $100, 184, 12, 45$ 출력 데이터로 가져옵니다. 오른쪽은 평균 풀링으로 각각의 $2 \times 2$의 범위 내 요소의 평균값인 $36, 80, 12, 15$ 를 출력 데이터로 가져옵니다. 풀링 층은 학습해야 할 매개변수가 없고 채널 수가 변하지 않으며 강건(Robust)하기 때문에 입력 변화에 영향을 적게 받는다는 특징을 가지고 있습니다.

Deep CNN

합성곱 신경망에서는 층을 깊게 쌓으면 어떤 이점이 있을까요? 각 합성곱 층마다 어떤 패턴을 학습하는 지를 시각화 해보면 신경망이 이미지를 어떤 방식으로 바라보는 지를 알 수 있습니다. 합성곱 신경망에서 연산이 일어나는 과정을 생각해보면 입력 데이터와 가까운 쪽의 합성곱 층은 이미지의 극히 일부 밖에 볼 수 없습니다. 하지만 층이 깊어지면 한 번에 이미지의 많은 부분을 볼 수 있습니다. 풀링 과정을 여러 번 거치면서 많은 픽셀 정보가 응축되기 때문입니다.

대표적인 합성곱 신경망 모델 중 하나인 알렉스넷(Alexnet)의 경우 1번째 합성곱 층에서는 엣지(Edge)나 블롭(Blob)등을 학습하고 3번째 층은 텍스쳐(Texture)를 학습합니다. 5번째 층에 다다르면 사물의 일부를 학습한다는 것으로 알려져 있습니다. 아래는 임의의 합성곱 신경망 내부에 있는 합성곱 층에서 학습하는 패턴을 시각화한 것입니다.

이미지 출처 : deeplizard.com

위 이미지는 입력 데이터와 가장 가까운 층으로 세로, 가로, 대각선 등의 엣지(Edge)를 학습하는 것을 알 수 있습니다.

이미지 출처 : deeplizard.com

위 이미지는 입력 데이터와 가장 멀리 떨어진 층, 즉 완전 연결 층과 연결된 합성곱 층으로 추상화된 사물의 형태를 패턴으로 학습하고 있는 것을 볼 수 있습니다.

이번 게시물은 “An overview of gradient descent optimization algorithms” 와 그의 번역인 “Gradient Descent Overview”를 참조하여 작성하였습니다.

Optimizer

가중치 초기화(Parameter initialization)를 통해서 시작점을 정했으니 하강하는 방법에 대해서 알아보겠습니다. 옵티마이저(Optimizer)는 최적화 방법을 결정해주는 방식입니다. 이번 게시물에서는 옵티마이저에 대해 알아보도록 하겠습니다. 우선 아래 이미지를 통해 어떤 옵티마이저가 있는지부터 알아보겠습니다.

이미지 출처 : slideshare.net/yongho

위 그림에서 위쪽 방향(파란색 화살표)은 어떤 방향으로 내려갈지를 개선하는 과정에서 탄생한 옵티마이저입니다. 아래쪽 방향(빨간색 화살표)는 얼마나 내려갈지(학습률)를 개선하는 과정에서 탄생한 옵티마이저이지요. 우리에게 익숙한 경사 하강법(Gradient descent, GD)을 개선한 확률적 경사 하강법부터 알아보도록 하겠습니다.

확률적 경사 하강법(Stochastic Gradient Descent, SGD)

경사 하강법은 학습에 모든 데이터를 다 사용합니다. 이 방법은 데이터셋이 커질수록 훨씬 더 많은 시간을 필요로합니다. 사용할 데이터셋이 100만건이라면 100만건의 데이터에 대해 모두 순전파를 계산하고 손실을 구한 뒤 이를 개선하는 방향으로 파라미터가 한 번 갱신됩니다. 당연히 시간이 많이 걸릴 수밖에 없겠지요. 이런 문제를 해결하기 위해서 등장한 것이 확률적 경사 하강법(Stochastic Gradient Descent, SGD)입니다.

확률적 경사 하강법

확률적 경사 하강법에서는 전체 데이터셋에서 하나의 데이터를 선택합니다. 그리고 이 데이터만을 사용하여 경사 하강법으로 개선해나갑니다. 대신 파라미터를 개선할 때마다 다른 데이터가 선택됩니다. 하나의 인스턴스만을 선택하여 학습하기 때문에 보통의 경사 하강법 보다 학습 속도가 훨씬 빠릅니다. 하지만 선택된 데이터가 아웃라이어일 수도 있겠지요. 이런 경우 오차가 급격히 증가하며 학습이 불안정해지는 단점을 가지고 있습니다. 아래는 확률적 경사 하강법과 경사 하강법을 비교하여 나타낸 그림입니다.

이미지 출처 : ankit-ai.blogspot.com

오른쪽에 있는 보통의 경사 하강법은 5번의 파라미터 갱신을 통해 최적점을 찾았습니다. 하지만 학습 데이터셋이 컸다면 한 번 갱신하는데 엄청난 시간이 걸렸을 것입니다. 반대로 확률적 경사 하강법은 17번이나 파라미터 갱신한 끝에 최적점을 찾았네요. 하지만 17개의 인스턴스만을 계산하여 얻어낸 결과입니다. 한 번 갱신할 때마다 데이터를 하나만 사용하기 때문에 계산이 매우 빠르지요. 확률적 경사 하강법의 수식은 아래와 같습니다.

[\theta \leftarrow \theta - \eta \nabla_\theta J(\theta;x^i;y^i)]

미니배치 경사 하강법

데이터를 하나만 사용하는 것은 상당히 불안합니다. 아웃라이어가 학습에 사용되는 날에는 최적점으로부터 엄청나게 멀어지게 되지요. 이런 단점을 해결하기 위한 것이 미니배치 경사 하강법(Mini-batch gradient descent)입니다. 하나의 인스턴스는 너무 불안정하니 $n$ 개의 인스턴스로 이루어진 미니배치를 학습 단위로 사용하자는 것이 미니배치 경사 하강법의 기본 아이디어입니다. 여러 개의 데이터를 사용하기 때문에 불안정성을 줄일 수 있다는 장점이 있습니다. 만약 배치 사이즈가 $100$이라면 그 안에 있는 데이터가 모두 아웃라이어일 확률은 매우 적어지겠지요.

$n$개의 인스턴스로 구성된 미니배치를 사용하는 미니배치 경사 하강법의 수식은 아래와 같이 나타낼 수 있습니다.

[\theta \leftarrow \theta - \eta \nabla_\theta J(\theta;x^{i:i+n};y^{i:i+n})]

한계점

확률적 경사 하강법은 한계점도 가지고 있습니다. 비등방성¹ 함수, 즉 방향에 따라 기울기 변화가 다른 함수에서 비효율적인 탐색 경로를 보여준다는 것이지요. 위 그림에서도 확률적 경사 하강법은 최적점까지 가는 데 훨씬 더 많은 갱신 횟수를 필요로 했습니다. 일반적인 경사 하강법보다는 빠르지만 여전히 비효율적이지요. 게다가 경향성에서 많이 벗어나는 데이터가 선택될 경우 국지적 최소점(Local minima)에 빠질 수 있다는 단점도 가지고 있습니다.

모멘텀(Momentum)

이런 한계점을 극복하기 위해 등장한 방법이 모멘텀(Momentum)입니다. 모멘텀의 우리말 뜻은 ‘운동량’입니다. 말 그대로 운동량을 최적화 과정에 적용합니다. 기울기가 큰 곳, 즉 그래디언트의 변화가 심한 구간에서는 값을 더 많이 개선합니다. 반대로 완만한 곳에서는 파라미터를 미세하게 개선해나가지요.

비등방성 함수에서 모멘텀을 적용했을 때와 그렇지 않을 때 확률적 경사 하강법이 어떻게 파라미터를 갱신하는지 알아보겠습니다.

이미지 출처 : researchgate.net

모멘텀을 적용했을 때 기울기가 급격하게 변하는 쪽(X축 방향)으로 더 많이 움직이는 것을 볼 수 있습니다. 덕분에 더 적은 갱신 횟수로도 최적점 가까이에 다가갈 수 있었지요. 수식을 통해 어떻게 최적점으로 빠르게 다가갈 수 있는지 알아보겠습니다.

[\begin{aligned} v_t &= \gamma v_{t-1} + \eta\nabla_\theta J(\theta)
\theta & \leftarrow \theta - v_t \end{aligned}]

위 식에서 $v_t$는 각 지점에서의 속도입니다. 확률적 경사 하강법의 식에 $\gamma \cdot v_{t-1}$ 이 더해졌습니다. 이전 갱신에서 구한 속도가 다음 속도에 영향을 미치게 되지요. $\gamma$ 는 모멘텀의 영향력을 얼마나 크게 할 것인지에 대한 하이퍼파라미터입니다. $\gamma = 0$ 이면 모멘텀을 적용하지 않은 확률적 경사 하강법과 같아지게 되며 이 값이 커질수록 모멘텀의 영향을 더 많이 받게 됩니다.

NAG

모멘텀을 다르게 적용하는 NAG(Nesterov Accelerated Gradient)라는 옵티마이저도 있습니다. NAG의 식은 다음과 같습니다.

[\begin{aligned} v_t &= \gamma v_{t-1} + \eta\nabla_\theta J(\theta - \gamma v_{t-1})
\theta &\leftarrow \theta - v_t \end{aligned}]

NAG 옵티마이저는 그래디언트의 변화를 그 자리에서 계산하지 않고 모멘텀에 의해서 이동한 곳에서 계산합니다. 모멘텀에 의해서 변화된 $\gamma \cdot v_{t-1}$ 을 빼준 곳, 즉 $(\theta - \gamma v_{t-1})$ 에서 그래디언트의 변화를 구합니다. NAG를 고안한 이유는 기존 모멘텀 적용 방식에 한 가지 문제가 있기 때문입니다. 최소점 부근에서 그래디언트 변화가 갑자기 클 때 최소점을 지나쳐 버리게 되지요. 하지만 NAG는 이전 위치에서 그래디언트를 계산하여 이런 사태에 대한 위험도를 낮추었습니다. 이런 개선을 통해 NAG는 오히려 최소점에 더욱 빠르게 도달할 수 있다는 장점을 가지고 있습니다. 다양한 NAG에 대한 설명은 이곳을 참고하면 좋습니다.

지금까지 확률적 경사 하강법과 이를 개선한 모멘텀, NAG를 알아보았습니다. 이 옵티마이저들은 모두 학습 방향을 어떻게 조정할 지 개선하는 과정에서 나왔습니다. 텐서플로우와 파이토치에서는 위 옵티마이저를 사용하기 위해서 아래와 같은 메서드를 제공하고 있습니다.

#TensorFlow
tf.keras.optimizers.SGD(
    learning_rate=0.01, momentum=0.0, nesterov=False, name='SGD', **kwargs
)

#Pytorch
torch.optim.SGD(
    params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False
)

Adagrad

다음으로 학습률(Learning rate)을 조정하여 성능을 개선한 몇 가지 옵티마이저에 대해서 알아보겠습니다. 이렇게 개선된 옵티마이저의 대표격이 바로 Adagrad(아다그라드)입니다. Adagrad는 ‘Ada’ptive ‘Grad’ient의 줄임말입니다. 적응형 그래디언트, 즉 파라미터마다 다른 학습률을 적용하겠다는 뜻이지요.

Adagrad는 자주 등장하는 특성의 파라미터에 대해서는 낮은 학습률을, 가끔 등장하는 특성의 파라미터에 대해서는 높은 학습률을 적용합니다. 희소한 데이터에 대해 이 방법을 적용할 경우 훨씬 더 강건(Robust)하다는 장점이 있지요.

Adagrad의 수식을 살펴보겠습니다. 특성의 파라미터마다 다른 값을 적용하므로 $i$ 번째 특성의 그래디언트를 $g_{t,i}$를 아래와 같이 표기하겠습니다.

[g_{t,i} = \nabla_\theta J(\theta_{t,i})]

각 파라미터 $\theta_i$의 갱신은 다음과 같은 식을 통해서 진행됩니다.

[\theta_{t+1, i} = \theta_{t, i} - \frac{\eta}{\sqrt{G_{t,ii}+\epsilon}}\cdot g_{t,i}]

아래 식에서 $G_t$는 $t$번째 학습에서 $\theta_i$에 대한 그래디언트 제곱의 합을 나타낸 것입니다. $\epsilon$은 계산의 안정성을 위한 작은 상수로 일반적으로는 $10^{-8}$을 사용합니다. 이를 모든 파라미터에 대한 식으로 일반화하면 다음과 같습니다.

[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{G_t+\epsilon}}\odot g_t]

위 식에서 $\odot$은 행렬의 원소별 곱셈을 의미합니다. 아래에서 일반적인 행렬곱과 원소별 곱을 비교해보겠습니다.

\[\begin{aligned} &\left[\begin{array}{cc} 1 & 2 \\ 3 & 4\end{array}\right] \cdot \left[\begin{array}{cc} 1 & 2 \\ 3 & 4\end{array}\right] = \left[\begin{array}{cc} 1\times1+2\times3 & 1\times2+2\times4 \\ 3\times1+4\times3 & 3\times2+4\times4\end{array}\right] = \left[\begin{array}{cc} 7 & 10 \\ 15 & 22\end{array}\right] \\ &\left[\begin{array}{cc} 1 & 2 \\ 3 & 4\end{array}\right] \odot \left[\begin{array}{cc} 1 & 2 \\ 3 & 4\end{array}\right] = \left[\begin{array}{cc} 1\times1 & 2\times2 \\ 3\times3 & 4\times4\end{array}\right]=\left[\begin{array}{cc} 1 & 4 \\ 9 & 16\end{array}\right] \end{aligned}\]

Adagrad는 학습률을 조정해주지 않아도 알아서 적절한 학습률을 적용한다는 장점이 있습니다. 하지만 단점도 존재합니다. $G_t$ 에 계속 양수가 더해지기 때문에 학습이 진행될수록 $G_t$값이 커지고 학습률이 점점 줄어들게 되지요. 이 때문에 많은 반복 학습 이후에는 파라미터가 거의 갱신되지 않는 문제가 발생합니다.

Adadelta & RMSprop

이런 문제를 해결하기 위해서 등장한 옵티마이저가 Adadelta와 RMSprop입니다.

Adadelta

먼저 Adadelta부터 알아보겠습니다. Adadelta는 학습률이 0에 가까워지는 문제를 해결하기 위해 모든 그래디언트의 제곱합인 $G_t$대신 이전 $w$개 만큼을 제곱하여 더한 값의 평균인 $E[g^2]_t$를 사용합니다. $E[g^2]_t$ 를 구하는 수식은 다음과 같습니다. $\gamma$은 비율을 조정하는 하이퍼파라미터이며 $0.9$ 정도로 설정합니다.

[E[g^2]t = \gamma E[g^2]{t-1} + (1-\gamma)g^2_t]

Adagrad의 수식을 먼저 써보고 Adadelta가 어떤 방식으로 이를 개선하는지 알아보겠습니다. 위에서 살펴본 Adagrad의 수식은 아래와 같았습니다.

[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{G_t+\epsilon}}\odot g_t]

Adadelta는 더 이상 $G_t$를 사용하지 않으므로 아래와 같이 식이 바뀌게 됩니다.

[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2]_t+\epsilon}}\cdot g_t]

분모 부분은 그래디언트의 제곱합에 루트를 취해준 것으로 간단히 제곱합의 제곱근(Root Mean Square)을 뜻하는 $RMS[g]_t$ 를 사용하여 아래와 같이 표현할 수도 있습니다.

[\theta_{t+1} = \theta_t - \frac{\eta}{RMS[g]_t}\cdot g_t]

Adagrad 논문의 저자는 단위를 맞추기 위해 그래디언트 $g_t$ 대신 파라미터의 변화량 $\Delta\theta$ 으로 표기하도록 하였습니다. 바꿔쓴 식은 아래와 같습니다.

[E[\Delta\theta^2]t = \gamma E[\Delta\theta^2]{t-1} + (1-\gamma)\Delta\theta^2t
RMS[\Delta\theta]_t = \sqrt{E[\Delta\theta^2]_t+\epsilon}
\theta{t+1} = \theta_t - \frac{\eta}{RMS[\Delta\theta]_t}\cdot g_t]

RMSprop

RMSprop은 Adadelta와 비슷한 시기에 등장한 옵티마이저입니다. 독립적으로 등장했지만 Adagrad에서 학습률이 사라지는 문제를 해결하고자 고안된 것이기 때문에 형태가 거의 동일합니다. RMSprop 옵티마이저의 수식 형태는 다음과 같습니다.

[E[g^2]t = 0.9 E[g^2]{t-1} + 0.1g^2t
\theta{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2]_t+\epsilon}}\cdot g_t]

위 식이 Adadelta의 첫번째 식에서 $\gamma = 0.9$로 고정한 것과 같음을 알 수 있습니다. 그래디언트의 변화를 조정하는 것도 동일합니다. RMSprop을 제시한 제프리 힌튼은 적정한 학습률 값으로 $\eta = 0.001$을 제시하였습니다.

Adam

Adam(Adaptive moment estimation, 아담)은 그래디언트 조정법(모멘텀, NAG 등)과 학습률 조정법(Adagrad, Adadelta, RMSprop)의 장점을 융합한 옵티마이저입니다. Adam은 그래디언트 $g_t$ 에 의해 변하는 중심(1차) 모멘텀 $m_t$와 분산(2차) 모멘텀 $v_t$를 사용합니다. 각 모멘텀은 다음과 같이 구할 수 있습니다.

[m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t
v_t = \beta_2 v_{t-1} + (1-\beta_2)g^2_t]

Adam의 저자들은 $m_t, v_t$ 를 단순히 위와 같이 설정할 때, 학습 초반 $(t \sim 0)$ 에서 $\beta_1,\beta_2 \approx 1$ 일 때의 값이 $0$ 으로 편향됨을 발견했습니다. 실제 식에는 편향을 보정한 $\hat{m_t}, \hat{v_t}$를 정의하여 사용하였습니다.

[\hat{m_t} = \frac{m_t}{1-\beta^t_1}
\hat{v_t} = \frac{v_t}{1-\beta^t_2}]

이를 활용한 Adam의 수식은 아래와 같습니다.

[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}\cdot \hat{m_t}]

저자들은 $\beta_1$ 의 기본값으로는 $0.9$ 를, $\beta_2$의 기본값으로 $0.999$ 를, $\epsilon$의 적정한 값은 $10^{-8}$ 을 제안했습니다.

Comparison

지금까지 알아본 옵티마이저가 아래는 2가지 형태의 손실 함수에서 최적화하는 방향과 속도를 시각화한 이미지입니다.

이미지 출처 : rnrahman.com/blog

지금까지 알아본 것 이외에도 AdaMax, Nadam, AdamW등 다양한 옵티마이저가 있습니다. 여러가지 옵티마이저 중 무엇을 사용하는 것이 좋을까요? Adam은 이전 옵티마이저의 문제를 해결하고자 나온 것이기에 초기에 고안된 SGD보다 대부분의 상황에서 좋은 성능을 보입니다.

하지만 “공짜 점심은 없다”라는 말은 모델뿐만 아니라 옵티마이저에도 적용되는 말입니다. 우선 데이터셋마다 가장 좋은 성능을 보이는 옵티마이저가 다릅니다. 손실 함수가 정말 단순한 형태를 가지고 있다면 Adam을 사용하는 것은 오히려 수렴을 늦추는 결과를 가져올 수도 있습니다. 같은 옵티마이저를 사용하더라도 하이퍼파라미터를 어떻게 설정하느냐에 따라서도 성능이 달라집니다. 그렇기 때문에 최대한 많은 방법을 시도해보고 그 중 가장 좋은 결과를 내주는 옵티마이저를 선택하는 것이 올바른 방법이라 할 수 있겠습니다.

이번 게시물은 “밑바닥부터 시작하는 딥러닝”과 “Weight Initialization Techniques in Neural Networks”를 참조하여 작성하였습니다.

Parameter Initialization

신경망 모델의 목적은 손실(Loss)을 최소화하는 과정, 즉 파라미터 최적화(Parameter optimization)입니다. 이를 위해서 손실함수에 대해 경사 하강법을 수행했습니다.

이를테면, 어떤 데이터셋의 손실 함수 그래프가 아래와 같이 생겼다고 해보겠습니다. 그런데 동일하게 경사 하강법을 따라서 내려가더라도 도달하는 최저점이 다른 것을 볼 수 있습니다.

이미지 출처 : medium.com/coinmonks

만약에 오른쪽 봉우리 어딘가에서 시작한다면 같은 지점에서 시작한다면 아래 새로 생긴 경로를 따라서 학습될 수도 있겠지요. 이 경로를 따라 나온 최저점은 앞선 두 결과의 최저점보다 훨씬 더 큽니다. 제대로 최적화되지 못한 것이지요.

이처럼 첫 위치를 잘 정하는 것도 좋은 학습을 위한 조건 중 하나입니다. 이 때문에 학습 시작 시점의 가중치를 잘 정해주어야 하지요. 상황에 맞는 적절한 가중치 초기화(Weight initialization)방법을 사용하게 됩니다. 고성능의 신경망 모델을 구축하기 위해 꼭 필요한 작업이지요. 그렇다면 가중치 초기화 방법에는 어떤 것이 있을까요?

Zero initialization

가장 먼저 떠오르는 생각은 “모든 파라미터 값을 0으로 놓고 시작하면 되지 않을까?” 입니다. 하지만 이는 너무나도 단순한 생각입니다. 좀 더 자세히 말하자면 신경망의 파라미터가 모두 같아서는 안됩니다.

파라미터의 값이 모두 같다면 역전파(Back propagation)를 통해서 갱신하더라도 모두 같은 값으로 변하게됩니다. 신경망 노드의 파라미터가 모두 동일하다면 여러 개의 노드로 신경망을 구성하는 의미가 사라집니다. 결과적으로 층마다 한 개의 노드만을 배치하는 것과 같기 때문이지요. 그래서 초깃값은 무작위로 설정해야 합니다.

Random Initialization

파라미터에 다른 값을 부여하기 위해서 가장 쉽게 생각해 볼 수 있는 방법은 확률분포를 사용하는 것이지요. 정규분포를 이루는 값을 각 가중치에 배정하여 모두 다르게 설정할 수 있습니다. 표준편차를 다르게 설정하면서 정규분포로 가중치를 초기화한 신경망의 활성화 함수 출력 값을 시각화해보겠습니다. 신경망은 100개의 노드를 5층으로 쌓았습니다.

먼저 표준편차가 $1$인 케이스를 알아보겠습니다. 활성화 함수로는 시그모이드(로지스틱) 함수를 사용하였습니다.

그림으로 보면 활성화 함수로부터 0과 1에 가까운 값만 출력되는 것을 볼 수 있습니다. 활성화 값이 0과 1에 가까울 때 로지스틱 함수의 미분값은 거의 0에 가깝습니다. 이렇게 되면 학습이 일어나지 않는 기울기 소실(Gradient vanishing) 현상이 발생하게 됩니다. 그렇다면 이렇게 값이 양 극단으로 치우치지 않도록 표준편차를 줄여보겠습니다. 아래는 표준편차를 $0.01$ 인 정규분포로 가중치를 초기화한 뒤에 활성화 함수의 출력값을 시각화한 것입니다.

하고자 했던 대로 기울기 소실 효과는 발생하지 않았습니다. 하지만 대부분의 출력값이 $0.5$ 주변에 위치하고 있네요. Zero initialization에서도 말했던 것처럼 모든 노드의 활성화 함수의 출력값이 비슷하면 노드를 여러 개로 구성하는 의미가 사라지게 됩니다.

Xavier Initialization

사비에르 초기화(Xavier initialization)는 위에서 발생했던 문제를 해결하기 위해 고안된 초기화 방법입니다. 사비에르 초기화에서는 고정된 표준편차를 사용하지 않습니다. 이전 은닉층의 노드 수에 맞추어 변화시킵니다. 이전 은닉층의 노드의 개수가 $n$ 개이고 현재 은닉층의 노드가 $m$ 개일 때, $\frac{2}{\sqrt{n+m}}$ 을 표준편차로 하는 정규분포로 가중치를 초기화합니다.

이전과 동일한 신경망에 가중치를 사비에르 초깃값으로 초기화한 뒤 활성화 값 그래프가 어떻게 나오는지 시각화 해보겠습니다.

활성값이 이전 두 방법보다 훨씬 더 고르게 퍼져있음을 볼 수 있습니다. 층마다 노드 개수를 다르게 설정하더라도 이에 맞게 가중치가 초기화되기 때문에 고정된 표준편차를 사용하는 것보다 훨씬 더 강건(Robust)합니다. 사비에르 초기화는 논문을 발표했던 사비에르 글로로트(Xavier Glorot)의 이름을 따서 만들어졌는데요. 성을 따서 글로로트 초기화로 불리기도 합니다. 텐서플로우와 파이토치에서는 각각 아래와 같이 사비에르 초기화를 적용할 수 있습니다.

# TensorFlow
tf.keras.initializers.GlorotNormal()

# PyTorch
torch.nn.init.xavier_normal_()

He Initialization

He 초기화(He Initialization)는 ReLU함수를 활성화 함수로 사용할 때 추천되는 초기화 방법입니다. 컴퓨터 비전(Computer vision) 분야의 대표적인 Pre-trained 모델인 VGG도 활성화 함수로 ReLU를 사용하고 있는데요. 그렇기 때문에 He 초기화를 적용하고 있습니다. He 초기화는 $\sqrt{\frac{2}{n}}$ 를 표준편차로 하는 정규분포로 초기화합니다.

아래는 활성화 함수가 ReLU 함수인 5층 신경망에서 사비에르 초기화를 적용했을 때 활성값이 어떻게 변하는 지를 나타낸 그래프입니다.

첫 번째 층에서는 활성화 값이 골고루 분포되어 있지만 층이 깊어질수록 분포가 치우치는 것을 볼 수 있습니다. 만약 층이 더 깊어진다면 거의 모든 값이 $0$에 가까워지면서 기울기 소실이 발생하게 됩니다. 그렇다면 He 초기화를 사용했을 때는 활성값이 어떻게 변하는지 알아보겠습니다.

층이 깊어지더라도 모든 활성값이 고른 분포를 보이는 것을 알 수 있습니다. 사비에르 초기화와 마찬가지로 He 초기화 역시 카이밍 히(Kaiming He)의 성을 따서 지어졌습니다. 이름을 따서 카이밍 초기화로 부르기도 합니다. 텐서플로우와 파이토치에서는 각각 아래와 같이 He 초기화를 적용할 수 있습니다.

# TensorFlow
tf.keras.initializers.HeNormal()

# PyTorch
torch.nn.init.kaiming_normal_()

Choice

지금까지 살펴본 것처럼 사용하는 활성화 함수에 따라 적절한 초기화 방법이 달라집니다. 일반적으로 활성화 함수가 시그모이드 함수일 때는 사비에르 초기화를, ReLU류의 함수일 때는 He 초기화를 사용합니다. 하지만 가중치 초기화 방법은 이외에도 많으며 절대적인 답이 정해져 있는 것은 아닙니다.

Back Propagation

이번 게시물에서는 신경망 정보 전달의 핵심인 순전파와 역전파에 대해서 알아보겠습니다. 이 두 가지가 잘 일어나야 정보가 제대로 전달되어 손실을 줄이는 방향으로 학습이 잘 일어날 수 있겠지요. 아래는 신경망의 대략적인 흐름을 나타낸 이미지입니다.

이미지 출처 : machinelearningknowledge.ai

Forward Propagation

순전파(Forward Propagation)은 (입력층 → 출력층)의 방향으로 계산하는 과정입니다. 신호와 가중치를 곱한 값 출력층까지 차례대로 계산합니다. 아래 이미지를 보면서 순전파의 계산이 어떻게 진행되는지를 알아보겠습니다. 입력층의 노드가 2개이고 은닉층의 노드가 3개, 출력층의 노드가 1개인 신경망이 있다고 해보겠습니다. 이 인스턴스의 신호 $x_1, x_2$ 의 값은 1이며 레이블 $y$ 는 0입니다.

이미지 출처 : packtpub.com/book/big_data_and_business_intelligence

모든 층에 활성화 함수로 시그모이드(로지스틱) 함수를 사용한다면 은닉층의 히든노드에 들어갈 값 $\text{Sigmoid}(h)$는 아래의 수식을 통해서 구할 수 있습니다. $h_1,h_2,h_3$ 은 위쪽 노드부터 활성화 함수에 들어가는 값을 나타냅니다.

[h_1 = 1 \times 0.8 + 1 \times 0.2 = 1.0, \quad \text{Sigmoid}(h_1) = 0.73
h_2 = 1 \times 0.4 + 1 \times 0.9 = 1.3, \quad \text{Sigmoid}(h_2) = 0.79
h_3 = 1 \times 0.3 + 1 \times 0.5 = 0.8, \quad \text{Sigmoid}(h_3) = 0.69]

이제 은닉층에 들어갈 값을 모두 구했으니 출력되는 값 $\hat{y}$ 를 구해보겠습니다.

[\hat{y} = 0.73 \times 0.3 + 0.79 \times 0.5 + 0.69 \times 0.9 = 1.235]

이렇게 출력값을 구해내기 까지의 과정을 순전파라고 합니다.

Back Propagation

위 순전파 과정에서 실제의 레이블 $y=0$ 이지만 예측 레이블은 $\hat{y} = 1.235$ 입니다. $1.235$ 의 오차가 발생했네요. 이제 손실 함수(Loss function)을 통해 계산한 손실을 줄이는 방향으로 학습할 차례입니다. 각 노드에 손실 정보를 전달하는 과정을 역전파(Back propagation)라고 합니다. 손실 정보는 (출력층 → 입력층)의 방향으로 전달되기 때문에 ‘역’전파라는 이름이 붙었습니다.

먼저 연쇄 법칙(Chain rule)에 대해 알아보겠습니다. 미분값을 전달하는 역전파를 이해하기 위해서는 필수적으로 알아야 하는 개념이지요. 연쇄 법칙은 합성 함수의 도함수를 각 함수의 도함수의 곱으로 나타내는 방식입니다. 간단한 예를 들어보겠습니다. 함수 $z = (x+y)^2$ 가 있다고 해보겠습니다. 이 함수를 전개한 뒤에 $x$ 로 편미분하면 아래와 같은 편도함수를 구할 수 있습니다.

[\frac{\partial z}{\partial x} = \frac{\partial (x^2 + 2xy+y^2)}{\partial x} = 2x + 2y]

이를 $t = x+y$ 를 사용하여 아래와 같이 치환한 뒤에 연쇄 법칙을 사용하여 편도함수를 구해보겠습니다.

[z = t^2, \quad t=x+y]

연쇄 법칙을 사용하면 $\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \frac{\partial t}{\partial x}$ 로 나타낼 수 있으므로 아래와 같이 편도함수를 구할 수 있습니다.

[\begin{aligned} \frac{\partial z}{\partial x} &= \frac{\partial z}{\partial t} \frac{\partial t}{\partial x}
&= 2t \cdot 1 = 2t \end{aligned}]

이제 본격적으로 역전파에 대해 알아보지요. 순전파에서 신경망이 수행하는 연산을 단순화하여 가중치 $x,y$ 로부터 출력 $z$를 내어 놓는 임의의 함수 $z = f(x,y)$ 라고 해보겠습니다. 원래의 손실 함수를 $L$이라고 하면 이를 개선하기 위한 미분은 $\frac{\partial L}{\partial z}$ 가 됩니다.

이를 각 가중치 $x, y$ 에 대하여 편미분한 값으로 나누어 가지게 됩니다. 아래는 이 과정을 잘 보여주는 그림입니다.

이미지 출처 : bishwarup307.github.io

역전파는 이 과정을 신경망의 모든 노드에 대해서 실행합니다. 예시를 통해 역전파가 일어나는 과정을 알아보겠습니다. 아래는 이진분류 문제에 대해서 100번의 반복 학습 동안의 노드의 가중치, 손실값, 결정 경계가 변하는 모습을 보여주는 이미지입니다.

이미지 출처 : tamaszilagyi.com

다음으로 가중치가 어디서부터 어떻게 개선되는 지를 결정하는 가중치 초기화(Weight initialization)와 옵티마이저(Optimizer)에 대해서 알아보도록 하겠습니다.

Learning

신경망(Neural net)은 파라미터를 더 좋은 방향으로 개선하도록 학습해나갑니다. 여기서 ‘더 좋은 방향’이란 무엇일까요? 우리가 길을 갈 때에도 목적지를 정하고 그 방향대로 나아가야 하듯 신경망에게도 나아가야 하는 ‘방향’이 있습니다. 이 때 방향을 결정하는 기준이 되는 것이 바로 손실 함수(Loss function)입니다. 이번 시간에는 손실 함수에 대해서 알아보도록 하겠습니다.

Loss function

신경망 노드 내의 파라미터가 어느 방향으로 개선되어야 할 지 판단하는 지표로 손실(Loss, Cost)을 사용합니다. 어떤 작업을 수행할 지에 따라 손실을 구하기 위한 손실 함수(Loss function, Cost function)이 달라집니다.

Mean Square Error (MSE)

회귀(Regression)에서는 손실 함수로 대개 평균 제곱 오차(Mean square error, MSE)를 사용합니다. 평균 제곱 오차는 실제 값과 예측값의 차이를 구한 뒤 제곱한 값을 모든 인스턴스에 대해 더한 것입니다. 아래는 평균 제곱 오차의 수식입니다.

[\text{Loss}_{MSE} = \frac{1}{2}\sum_k{(\hat{y}_k - y_k)^2}]

위 식에서 $\hat{y}_k$는 신경망이 출력하는 값, 즉 예측값입니다. $y_k$는 실제 데이터가 가지고 있는 레이블입니다. $k$는 데이터의 개수입니다. 아래는 각 인스턴스에 대해 평균 제곱 오차를 시각화하여 나타낸 것입니다. 아래 이미지에서 빨간 막대의 길이를 제곱한 뒤 모두 더해준 값을 반으로 나눈 값이 평균 제곱 오차값이 됩니다.

이미지 출처 : freecodecamp.org

평균 제곱 오차는 직관적이고 이해하기 쉽습니다. 도함수 식의 계산도 쉽기 때문에 회귀의 손실 함수로 주로 사용됩니다.

Cross-Entropy Error

이진 분류(Classification)에서는 교차 엔트로피 오차(Cross-entropy error, CEE)를 주로 사용합니다. 교차 엔트로피 오차를 사용하여 구한 오차를 수식으로 나타내면 아래와 같습니다.

[\text{Loss}_{CEE} = -\sum_k{y_k\log_2{\hat{y}_k}}]

교차 엔트로피 오차는 어떻게 작용할까요? 실제 레이블이 $\left[\begin{array}{ccccc}1 & 0 & 0 & 0 & 0\end{array}\right]$ 인 5개의 인스턴스에 대하여 2개의 분류기가 각각 다음과 같이 예측값을 내놓았다고 가정하겠습니다.

[\text{Classifier 1} : \left[\begin{array}{ccccc}1 & 0 & 0 & 0 & 0\end{array}\right]
\text{Classifier 2} : \left[\begin{array}{ccccc}0 & 0 & 0 & 0 & 0\end{array}\right]]

분류기1은 실제 레이블과 동일한 예측값을 내놓았습니다. 하지만 분류기2는 하나의 인스턴스에 대해 잘못 예측했네요. 각 분류기에 대해 교차 엔트로피 오차를 구해보겠습니다. ( $\log_2 0 = -\infty$ 이므로 $0$ 대신 매우 작은 값인 $2^{-10^{10}}$을 대입하여 $\log_2 2^{-10^{10}} = -10^{10}$으로 대체하겠습니다.)

[\begin{aligned} L_1 &= -(1\log1 + 0\cdot \log 2^{-10^{10}} + 0\cdot \log 2^{-10^{10}} + 0\cdot \log 2^{-10^{10}} + 0\cdot \log 2^{-10^{10}})
&= - (1\cdot 0 + 0\cdot -10^{10} +0\cdot -10^{10}+0\cdot -10^{10}+0\cdot -10^{10})= 0
L_2 &= -(1\cdot \log 2^{-10^{10}} + 0\cdot \log 2^{-10^{10}} + 0\cdot \log 2^{-10^{10}} + 0\cdot \log 2^{-10^{10}} + 0\cdot \log 2^{-10^{10}})
& = - (1\cdot -10^{10} + 0\cdot -10^{10} +0\cdot -10^{10}+0\cdot -10^{10}+0\cdot -10^{10})= 10^{10} \end{aligned}]

레이블을 모두 맞춘 첫 번째 분류기의 교차 엔트로피 오차는 $0$ 이 나옵니다. 하지만 하나를 틀린 두 번째 분류기의 교차 엔트로피 오차는 매우 큰 값이 나왔습니다. 교차 엔트로피 오차의 식에는 로그 함수 $\log_2x$ 가 있습니다. 로그 함수는 $0$으로 갈 때 급격하게 값이 $-\infty$로 발산하는 특성이 있습니다. 교차 엔트로피 오차는 이런 특성을 사용하여 레이블을 잘못 예측했을 때 엄청 큰 손실 값을 배정합니다. 아래는 로그 함수의 그래프입니다.

이미지 출처 : wikipedia - Logarithm

Gradient Descent

손실 함수의 값은 말 그대로 손실(Loss)입니다. 이 값이 크면 신경망 모델의 성능이 좋지 않다는 뜻입니다. 그렇기 때문에 학습은 손실 함수의 값을 줄이는 방향으로 진행해야 하지요. 신경망에서는 파라미터를 개선하는 방법으로 경사 하강법(Gradient descent method)을 사용합니다.

Gradient

경사 하강법이 뭐길래 손실 함수의 값을 낮추기 위해 이 방법을 사용하는 것일까요? 실제 고차원 데이터를 다룰 때 손실 함수의 그래프는 아래와 같이 생겼습니다. 손실 함수의 최솟값은 아래 그림에서 가장 낮은 지점이 됩니다. 이 지점을 찾기 위해서 점점 아래로 구슬이 굴러가듯 경사를 따라 내려가는데 이를 경사 하강법이라고 합니다.

이미지 출처 : medium.com

경사 하강법을 하려면 우선 경사(기울기)를 먼저 알아야겠죠. 경사는 미분을 사용하여 구합니다. 임의의 미분가능한 함수 $f(x)$의 도함수는 다음과 같이 구할 수 있습니다.

[\frac{df(x)}{dx} = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}]

변수가 2개 이상일 때는 편미분(Partial derivative)을 사용합니다. 편미분은 특정 변수 하나에 초점을 맞추어 미분을 하는 방식입니다. 다른 모든 변수는 상수로 취급하고 일변수 함수의 미분 방법을 적용합니다. 간단한 예를 들어보겠습니다. 다변수 함수 $g(x, y, z) = 3 x^2 y + x y^2 z + 2x + yz$ 가 있다고 해보겠습니다. 이를 $x$ 에 대해 편미분하면 다음과 같은 식이 도출됩니다.

[\frac{\partial g(x,y,z)}{\partial x} = 6xy + y^2z + 2]

손실 함수의 변수가 여러 개일 때 각 변수에 대한 편미분을 벡터로 묶어 정리한 것을 그래디언트(Gradient)라고 합니다. 예를 들어, $h(x_1, x_2, \cdots, x_n)$ 과 같이 변수가 $n$ 개인 함수의 그래디언트는 다음과 같이 나타나게 됩니다.

[\nabla_x h(x) = \bigg[\frac{\partial h(x)}{\partial x_1}, \frac{\partial h(x)}{\partial x_2}, \cdots, \frac{\partial h(x)}{\partial x_n}\bigg]]

Descent

그래디언트를 알았으니 이제 하강(Descent)을 알아볼 시간입니다. 실제로 맞닥뜨리는 손실 함수는 부분적으로 컨벡스(Convex, 볼록) 함수입니다. 컨벡스 함수가 무엇인지는 아래의 그래프를 통해서 알아보겠습니다.

이미지 출처 : wikipedia - convex function

2차원 평면상에서 컨벡스 함수 $f(x)$는 다음의 조건을 만족합니다. $f(x)$ 위의 두 점 $(x_1, f(x_1)), (x_2, f(x_2))$ 을 잇는 직선을 $g(x)$ 라 하겠습니다. 이 때, 구간 $(x_1, x_2)$ 사이의 점 $x_m$ 에서 $f(x) < g(x)$ 입니다. 3차원 컨벡스 함수는 어떻게 생겼을까요? 아래에 3차원 컨벡스 함수가 있습니다.

이미지 출처 : wikipedia - convex function

우리 목적은 구슬이 굴러 내려가듯 내리막길을 따라 최저점(Minimum)에 다다르는 것이었습니다. 컨벡스 함수에서는 어떤 점에서 시작하더라도 내리막으로만 움직인다면 최저점에 도착할 수 있지요. 함수 $f(x)$의 기울기를 따라 내려가는 과정, 즉 경사 하강법을 수식으로 나타내면 다음과 같습니다. 아래 식에서는 변수 $x_i$ 에 대해서 편미분한 기울기만을 사용하였습니다.

[x_{i,j+1} := x_{i,j} - \eta \frac{\partial f(x)}{\partial x_{i,j}}]

구슬이 굴러가는 비유대신 한 발짝씩 산을 내려가는 과정으로 생각해보겠습니다. 위 식에서 좌변에 있는 $x_{i,j+1}$ 는 새로 발을 내딛을 위치입니다. 우변에 있는 $x_i$ 는 현재 자신이 서있는 위치입니다. $\frac{\partial f(x)}{\partial x_i}$ 는 그 위치에서의 기울기가 되겠지요. 우리는 내려가야 하므로 원래 위치 $x_{i,j}$ 에 기울기를 빼주어 새로운 위치 $x_{i,j+1}$ 을 정하게 됩니다.

그렇다면 $\eta$ 는 무엇일까요? $\eta$ 는 학습률(Learning rate)입니다. 이 하이퍼파라미터(Hyperparameter)는 기울기를 따라 얼마만큼 내려갈지를 결정합니다. 이 값이 너무 작으면 최저점을 찾아가는데 오랜 시간을 필요로합니다. 심한 경우에는 주어진 반복(iteration) 내에서 최저점을 찾지 못하기도 하지요. 반대로 학습률이 너무 크면 최저점을 지나쳐버립니다. 제대로 된 학습을 하지 못하거나 발산해버리는 문제가 발생하지요.

반지름이 1m인 구덩이가 있을 때, 개미와 공룡이 이 구덩이의 최저점을 향해 나아간다고 생각해보겠습니다. 개미가 중심까지 가려면 엄청 오랜 시간이 걸릴 것이고, 공룡은 중심을 지나보지도 못하고 휙 지나쳐 버리겠지요. 아래는 학습률이 너무 작을 때와 클 때 $x_j$ 가 어떻게 변하는지를 보여주는 이미지입니다.

이미지 출처 : srdas.github.io

제대로된 학습을 위해서는 적절한 학습률 찾아야만 합니다. 그렇기 때문에 처음에는 큰 학습률을 사용하다가 점점 줄이는 학습률 감쇠(Learning rate decay) 등의 다양한 전략을 사용합니다. 이곳에서 경사 하강법에 대한 더 자세히 알아볼 수 있습니다.