해당 포스트는 스탠포드 대학교의 cs224w 를 바탕으로 작성하였습니다.

Graph Representation

이전 게시물에서 알아본 바와 같이 그래프는 노드와 엣지로 구성되어 있습니다. 노드(Node)는 특정 객체(Objects)를 나타내며 앞 스펠링을 따서 $N$ 으로 표현합니다. 엣지(Edge)는 링크(Link)라고도 불리며 노드 사이의 상호작용(Interaction)을 나타냅니다. 엣지 역시 맨 앞 스펠링을 따서 $E$로 표현합니다. 객체와 객체 간 상호작용으로 이루어진 시스템을 그래프라고 하며 $G(N,E)$ 로 나타냅니다. 그래프는 공용 언어이기 때문에 다양한 도메인에서의 시스템을 그래프로 설명할 수 있습니다.

우리가 접하게 되는 시스템을 그래프로 나타내고자 한다면 어떤 것을 노드로 나타내고, 어떤 것을 엣지로 나타낼 지를 결정해야 합니다. 물론 객체와 그 상호작용이 명확하고 유일한 시스템도 있지만, 그렇지 않은 시스템도 많습니다. 후자의 경우 어떤 노드로 설정하고 그 사이의 어떤 상호작용을 어떻게 나타낼 지, 즉 적절한 그래프 표현을 찾는 지가 굉장히 중요한 문제가 됩니다.

Directed vs Undirected

그래프를 구분하는 여러가지 범주 중 하나는 해당 그래프의 엣지가 방향성을 가지는가 입니다. 먼저 엣지가 방향성을 가지지 않는 그래프에 대해서 알아보겠습니다. 이런 그래프를 무향 그래프(Undirected graph)라고 합니다. 예를 들어, 페이스북에서의 친구 관계가 여기에 해당합니다. 반대로 엣지가 방향성을 가지는 그래프도 있는데 이런 그래프를 유향 그래프(Directed graph)라고 합니다. 트위터에서의 팔로우 관계나 금융 거래 등을 유향 그래프로 나타낼 수 있습니다. 아래는 유향 그래프와 무향 그래프의 구조를 나타낸 이미지입니다.

이미지 출처 : raywenderlich.com

Node degree

Node degree란 특정 노드 $i$ 와 인접한 노드의 수를 나타내는 척도로 $k_i$ 로 나타냅니다. 예를 들어, 아래와 같은 무향 그래프가 있을 때 붉은 색으로 표시된 노드의 Node degree는 $k_{\text{red}} = 4$ 입니다.

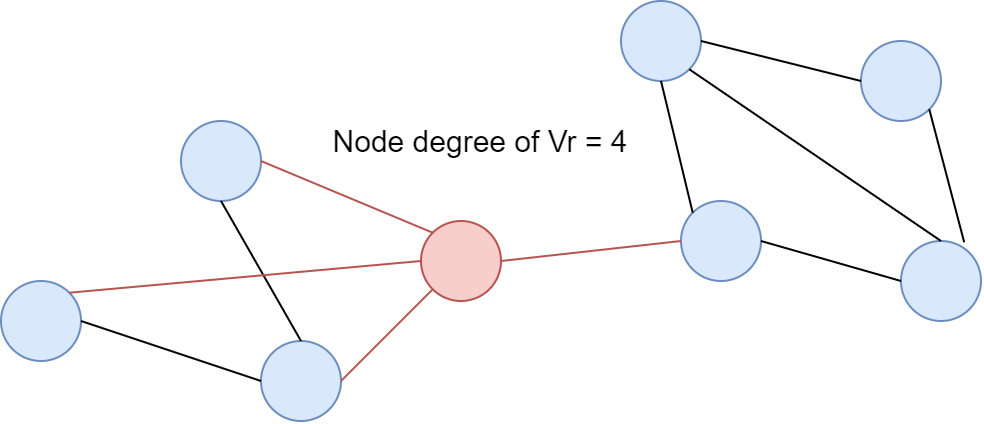
이미지 출처 : laptrinhx.com

이로부터 그래프 전체에서의 평균 Node degree, $\bar{k}$ 도 구할 수 있습니다. 엣지의 개수가 $E$ 이고 노드의 개수가 $N$ 일 때, 평균 Node degree는 아래 식을 사용하여 구할 수 있습니다.

[\bar{k} = \frac{1}{N} \sum_{i=1}^N k_i = \frac{2E}{N}]

유향 그래프(Directed graph)에서는 엣지 방향에 따라 in-degree, $k^{\text{in}}$ 와 out-degree, $k^{\text{out}}$ 를 따로 정의할 수 있습니다. 해당 노드로 들어오는 엣지의 개수를 in-degree 라고 하며, 해당 노드로부터 나가는 엣지의 개수를 out-degree 라고 합니다. 아래와 같은 유향 그래프가 있다고 해보겠습니다.

위 그림에서 붉은 색으로 표시된 $C$ 노드의 in-degree, $k_{\text{red}}^{\text{in}}=0$ 이고 out-degree $k_{\text{red}}^{\text{out}}=4$ 입니다. $C, D$ 처럼 $k^{\text{in}}=0$ 인 노드를 Source 라고 하고 $A,B,E$ 처럼 $k^{\text{out}}=0$ 인 노드를 Sink 라고 합니다. 유향 그래프에서의 Node degree는 다음과 같은 식을 만족합니다.

[k_c = k^{\text{in}} + k^{\text{out}}
\bar{k}^{\text{in}} = \bar{k}^{\text{out}} = \frac{E}{N}]

Bipartite Graph

이번에는 특이한 형태의 그래프인 이분 그래프(Bipartite graph)에 대해서 알아보도록 하겠습니다. 이분 그래프의 노드는 겹치지 않는 2개의 집합 $U, V$ 로 나눌 수 있습니다. 엣지는 $U$ 와 $V$ 사이만을 연결합니다. 즉, $U$ 에 속하는 노드 사이, $V$ 에 속하는 노드 사이에는 엣지 연결이 없습니다. 그림으로 나타내면 다음과 같습니다.

이미지 출처 : wikipedia.org

이분 그래프로 표현할 수 있는 관계는 논문 저자-논문, 출연배우-영화 등이 있습니다. 이분 그래프를 알아야 하는 이유는 이분 그래프로부터 $U,V$ 에 속하는 노드의 관계를 사영(Projection)할 수 있기 때문입니다. 아래와 같이 파란색으로 나타낸 사용자(Users) 노드 집합과 빨간색을 나타낸 상품(Items) 노드 사이의 관계를 나타낸 이분 그래프가 있다고 해보겠습니다.

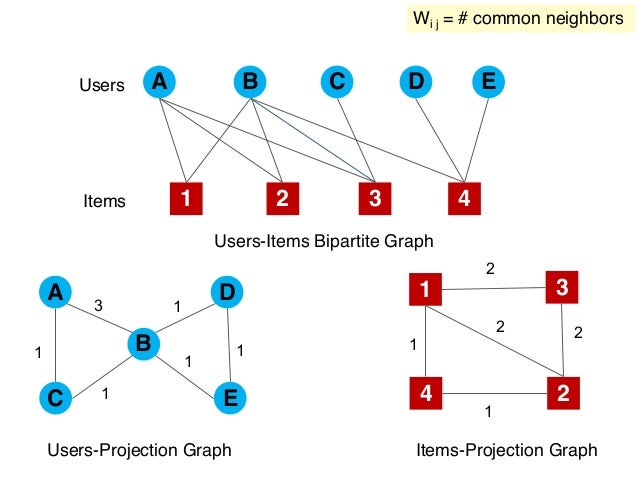
이미지 출처 : slideshare.net

사용자-상품 이분 그래프로부터 유저 간의 관계, 상품 간의 관계를 나타낸 그래프를 사영할 수 있습니다. 예를 들어, 유저 $A, B$ 는 3개의 상품을 공유하고 있으므로 3의 관계를 나타내는 노드로 연결합니다. 유저 $B, D$ 는 1개의 상품을 공유하고 있으므로 1의 관계를 나타내는 노드로 연결하며 유저 $A, D$ 는 아무런 상품도 공유하고 있지 않으므로 연결되지 않습니다. 상품 간의 관계를 나타낸 사영 그래프 역시 해당 상품이 몇 명의 유저를 공유하는 지를 바탕으로 서로의 관계를 나타냅니다.

Adjacency Matrix

이제는 위와 같이 나타나는 그래프를 컴퓨터가 이해할 수 있는 숫자로 표현해 줄 차례입니다. 그래프의 표현은 인접 행렬(Adjacency matrix)을 사용합니다. 가장 간단한 표현 방법은 연결 유무에 따른 이진 행렬(Binary matrix)입니다. 두 노드가 연결되어 있으면 1로, 그렇지 않으면 0으로 표현하는 방법이지요. 무향 그래프를 인접 행렬로 나타내면 아래와 같습니다.

이미지 출처 : thecrazyprogrammer.com

무향 그래프는 이어진 노드의 관계가 서로 동일하므로 인접 행렬 $A$ 의 대칭 성분이 동일합니다. 그렇기 때문에 무향 그래프를 나타낸 인접 행렬은 대칭 행렬(Symmetric matrix)이라는 특징이 있습니다. 그렇다면 유향 그래프는 인접 행렬로 어떻게 나타낼 수 있을까요? 유향 그래프를 나타낸 인접 행렬은 다음과 같습니다.

이미지 출처 : thecrazyprogrammer.com

유향 그래프를 나타낸 인접 행렬의 요소는 $i$ 번째 행의 노드가 $j$ 행의 노드를 가리킬 때에만 1의 값을 갖습니다. 예를 들어, 노드 2는 노드 1을 가리키기 때문에 $A_{21} = 1$ 로 나타냅니다. 하지만 노드 1은 노드 2를 가리키지 않기 때문에 $A_{12} = 0$ 으로 나타냅니다. 그렇기 때문에 유향 그래프를 나타낸 인접 행렬은 대부분 비대칭(Asymmetric)입니다.

현실 세상에 있는 네트워크를 나타낸 인접 행렬은 매우 희소합니다. 아래는 실제 네트워크에서의 노드 개수 $N$ 와 엣지 개수 $L$ , 평균 Node degree를 나타낸 표입니다.

인접 행렬에서 1의 비율은 $E/N^2$ 로 나타낼 수 있습니다. 위에 나온 대부분의 네트워크가 $10^{-4}$ 이하의 값을 가지므로 매우 희소한 인접 행렬로 나타난다는 것을 알 수 있습니다.

Attributes

각 노드와 엣지에는 여러 속성이 추가될 수 있습니다. 속성의 종류에는 다음과 같은 것들이 있습니다.

• 가중치(Weight) : 객체 간 의사소통을 나타낸 네트워크에서 네트워크의 빈도를 가중치로 표현할 수 있습니다.
• 순위(Ranking) : 객체 간 관계에 순위가 있을 경우 순위 속성을 사용하여 나타낼 수 있습니다.
• 유형(Type) : 객체 간 관계의 유형이 다를 경우 이를 속성으로 추가하여 표현할 수 있습니다.
• 부호(Sign) : 우호 관계, 적대적 관계와 같이 완전히 반대의 관계를 가질 경우 부호 속성을 추가하여 Positive/Negative 관계를 표현할 수 있습니다.

More Types of Graph

더욱 다양한 유형의 그래프에 대해서 알아보겠습니다. 첫 번째는 속성이 추가된 그래프입니다. 이 경우 인접 행렬은 $0,1$ 외에 다른 값을 가지게 됩니다. 가중치 속성이 추가된 행렬을 인접 행렬로 나타낸 그래프는 다음과 같습니다.

이미지 출처 : thecrazyprogrammer.com

Self-loops 가 추가된 형태의 그래프도 있습니다. Self-loops 가 없는 경우 인접 행렬의 대각(Diagonal) 성분은 항상 0이 되지만, 있을 경우에는 대각 성분 $A_{ii} \neq 0$ 이 됩니다.

이미지 출처 : quora.com

위 그래프에서 노드 1에 자기 자신을 가리키는 엣지가 하나있기 때문에 $A_{11} = 1$ 의 값을 갖습니다.

마지막으로 1개 이상의 노드로 연결된 다중 그래프(Multigraph)가 있습니다. 다중 그래프의 인접 행렬은 가중치 속성이 추가된 그래프와 같이 1이상의 값을 갖습니다.

이미지 출처 : math.stackexchange.com

Connectivity

그래프의 표현을 위해 마지막으로 알아볼 것은 연결성(Connectivity)입니다. 어떤 두 노드를 선택하더라도 둘을 연결하는 경로를 찾을 수 있을 경우 이 그래프를 연결된 그래프(Connected graph)라고 합니다. 위에서 예시로 살펴본 모든 그래프는 연결된 그래프입니다. 아래는 연결된 그래프와 연결되지 않은 그래프(Disconnected grpah)를 나타낸 이미지입니다.

이미지 출처 : algorithms.tutorialhorizon.com

유향 그래프에서 특정한 연결을 가진 노드 관계를 강한 연결(Strong connectivity)로 나타낼 수 있습니다. 아래와 같이 어떤 두 노드 $A, B$ 를 선택하더라도 두 노드 사이의 경로 $A \rightarrow B, B \rightarrow A$ 가 모두 정의될 경우 강하게 연결된 그래프(Strongly connected graph)라고 합니다.

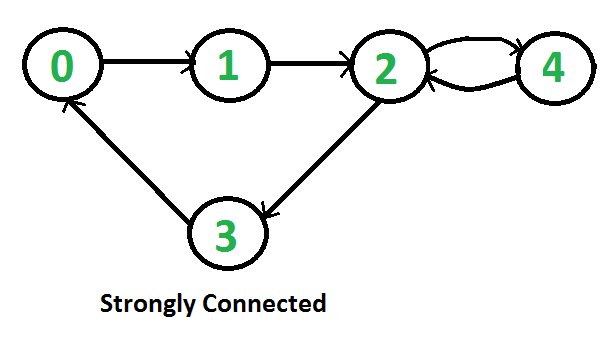
이미지 출처 : geeksforgeeks.org

예를 들어, 위 그래프에서 노드 1과 노드 3 사이의 경로는 $1 \rightarrow 3 \quad (=1\rightarrow2\rightarrow3)$ 과 $3 \rightarrow 1 \quad (=3\rightarrow0\rightarrow1)$ 이 모두 정의됩니다. 위 그래프의 어떤 두 노드를 선택하더라도 서로 간 경로가 정의되므로 강한 연결성(Strong connectivity)을 가진다고 할 수 있습니다.

범위를 좁혀 일반 그래프 내에서 강하게 연결된 부분(Strongly connected components, SCCs)을 정의할 수 있습니다. 일반 그래프에서 강한 연결을 가지는 노드 부분을 찾을 수 있는데 이를 SCC라고 합니다. 아래는 특정 그래프에서 SCC를 나타낸 이미지입니다.

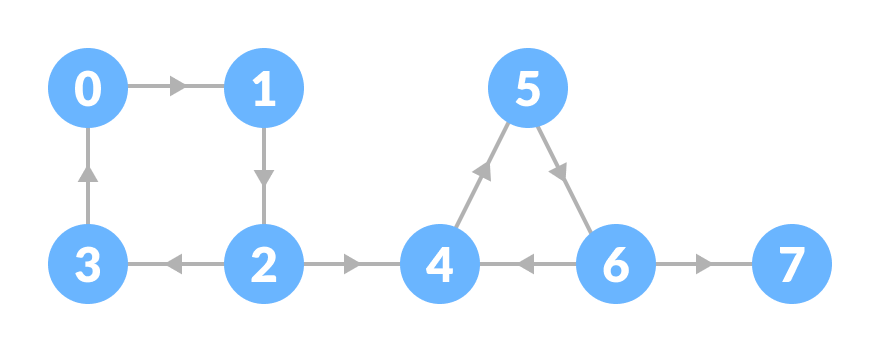
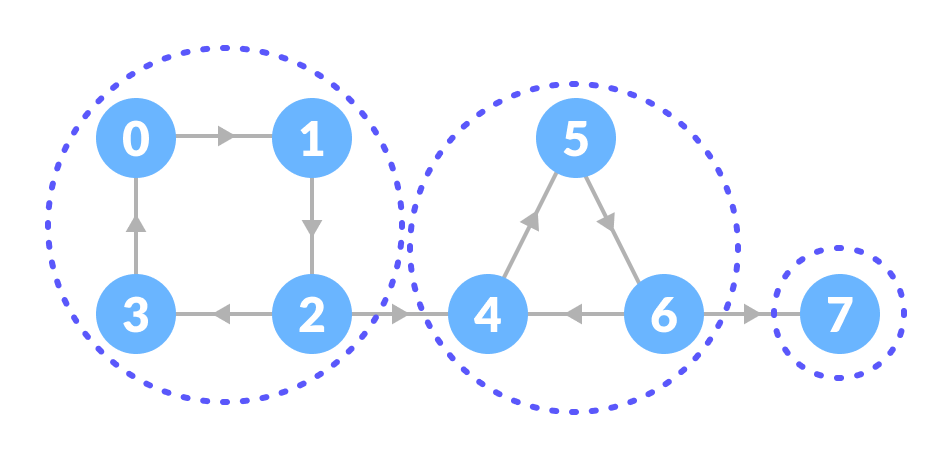
이미지 출처 : programiz.com

해당 포스트는 스탠포드 대학교의 cs224w 를 바탕으로 작성하였습니다.

Introduction to Graph ML

앞으로 그래프를 사용한 머신러닝 방법에 대해서 배워볼 것입니다. 그래프를 알아야 하는 이유는 무엇일까요?

Why Graph?

그래프는 노드(Node)와 엣지(Edge)의 형태로 구성되어 있는데요. 이와 같은 구조는 개체, 그리고 개체 사이에 상호작용을 묘사하고 분석하는 데 효과적입니다. 그래프로 나타내어지는 정보는 굉장히 많은데요. 대표적으로는 아래와 같은 것이 있습니다. 모두 해당 도메인 내에 있는 개체, 그리고 개체 사이에 일어나는 상호작용을 나타내고 있습니다.

이미지 출처 : web.stanford.edu/class/cs224w/slides/01-intro.pdf

작게는 원자와 원자 사이의 상호작용을 통해 형성되는 분자(Molecule)부터, 크게는 우주에서 별과 별, 별과 행성 등 다양한 개체가 이루는 상호작용을 그래프로 나타낼 수 있습니다. 소셜 네트워크를 나타내는 그래프는 우리에게 상당히 친숙한 그래프 구조 중 하나입니다.

크게는 두 가지 형태로 나누어 볼 수 있습니다. 첫 번째는 자연스럽게 그래프로 표현되는 것들입니다. 이를 Network라고 부르며 Natural Graph라고 부르기도 합니다. 소셜 네트워크, 커뮤니케이션 네트워크, 뉴런의 네트워크 등이 있습니다. 두 번째는 그래프로 표현 지어진 것들입니다. 대표적으로 지식 그래프나 3D shape가 이에 속합니다. 물론 둘 사이의 경계가 희미하기 때문에 모든 그래프 구조를 두 범주 내에 굳이 넣어야 하는 것은 아닙니다.

그렇다면 그래프 구조를 바탕으로 학습을 진행했을 때 얻을 수 있는 이점은 무엇이 있을까요? 가장 큰 이점은 관계가 명시적으로 드러나 있기 때문에 모델의 성능을 더욱 높일 수 있다는 것입니다. 하지만 그래프 형태의 단점 역시 존재하는데요. 기존 딥러닝이 잘 처리하는 텍스트나 이미지와는 다른 특성 때문에 모델에 집어넣기가 힘들다는 단점이 있습니다. 기존 딥러닝 모델은 텍스트-음성과 같은 선형 구조의 데이터나 이미지와 같은 그리드 형태의 데이터 처리에 특화되어 있지요. 하지만 그래프는 크기와 위상이 모호하며 공간적 지역성이 없기 때문에 딥러닝 모델에 바로 학습시키기 어렵다는 단점이 있습니다.

Application of Graph ML

머신 러닝은 무언가를 예측(Prediction)하는 일을 수행합니다. 그렇다면 Graph ML은 어떤 것을 예측할까요? Graph ML의 예측 범위는 다양합니다. 간단하게는 노드 혹은 엣지 수준의 예측을 수행할 수 있습니다. 하지만 이를 넘어 노드 쌍, 서브 그래프(Subgraph), 그리고 그래프 전체 수준의 예측이나 생성을 하기도 합니다.

노드 수준의 분류 태스크의 예시로는 추천 시스템에서 특정 유저에게 추천할 아이템의 범주를 예측하는 것이 있겠습니다. 다음으로 링크 수준의 예측은 지식 그래프에서 두 노드 사이에 어떤 관계가 있는 지를 예측할 때 사용됩니다. 복잡한 분자의 성질(Molecule property)을 예측할 때에는 그래프 수준의 분류가 사용됩니다. 특정 노드들이 집단을 형성하는지 알고 싶을 때에는 군집(Clustering) 태스크를 하기도 합니다. 또한 신약을 발견하기 위한 연구에서는 그래프 생성(Graph generation)이 사용되기도 합니다. 각각에 대해 조금 더 자세한 예시를 통해 알아보겠습니다.

Node-level Tasks

노드 레벨의 예측 태스크 중 주목할 만한 사례는 단백질의 3D 접힘 구조 예측입니다. 지난 2020년, DeepMind 팀은 알파폴드2를 발표했습니다. 해당 블로그 에서 알 수 있는 것처럼 연구진은 단백질 구조 예측에 Graph ML 방법론을 적용하였습니다. 단백질은 각각의 아미노산의 배열(Sequence)로 이루어지지만 어떤 배열을 가지는지에 따라 지역적으로 서로가 상호작용하는 정도가 달라집니다. 그래서 3차원 공간 상에서 각 단백질은 매우 다른 구조를 띠게 되고 이에 따라 단백질의 성질이 결정됩니다. 아래는 단백질 구조가 바뀌는 것을 잘 나타낸 그림입니다.

이미지 출처 : deepmind.com

그렇기 때문에 특정 아미노산 배열로 이루어진 단백질의 3차원 구조를 예측하는 것은 생물학에서 굉장히 중요한 연구 주제였는데요. 알파폴드는 이를 공간상에서의 그래프(Spatial graph)로 해석하면서 풀어낼 수 있었습니다.

Edge-level Tasks

추천 시스템을 만들 때 특정 유저가 아직 만나지 않은 특정 상품에 대해 어떤 반응을 보일 지 예측하는 것은 중요합니다. 예를 들어 서비스에 새로 등록된 상품이 있을 때, 굳이 이 상품을 좋아할 것 같지 않은 유저에게 먼저 보여줄 필요는 없겠지요. 그렇기 때문에 아직 연결고리가 없는 유저-상품에 대해 어떤 상호작용을 배정할지는 추천 시스템에서 중요한 문제입니다. 이런 문제를 풀기 위해서 유저라는 노드와 상품이라는 노드를 잇는 엣지를 예측하는 태스크가 사용됩니다.

약물의 부작용을 예측하고자 할 때에도 엣지 레벨의 예측 방법이 적용됩니다. 예를 들어, 2가지 약물을 동시에 복용했을 때 두 약물 이 몸 속 단백질과 특정 상호작용을 일으켜 부작용을 일으킬 수 있습니다. 따라서 두 약물이 동시에 복용하여도 아무런 문제가 없을지에 대해서 약물과 단백질을 노드로 설정한 다음, 약물-약물, 약물-단백질, 단백질-단백질 사이의 상호작용 중에서 아무런 문제가 발생하지 않는 지를 엣지 레벨 수준에서 예측합니다.

Subgraph-Level, Graph Level Tasks

도심의 교통 체증을 예측하는 태스크는 서브 그래프 수준의 예측을 수행합니다. 도로 사이의 특정 지점을 노드로 설정한 뒤에 해당 지점 사이의 도로를 링크로 연결합니다. 그리고 어떤 부분에서 정체가 발생할 지, 추후 교통 상황이 어떻게 변할 지를 서브 그래프 수준에서 예측하게 됩니다.

신약 개발에서는 그래프 전체 수준의 예측을 수행합니다. 각 원자를 노드로 설정하고 원자 사이의 화학 결합을 링크로 설정하여 원하는 성질을 가지기 위한 분자 구조를 예측하는 등의 태스크를 수행합니다. 이외에도 입자가 공간 상에서 어떻게 움직이는지에 대해 물리 시뮬레이션하는 태스크에서도 그래프 수준의 태스크가 사용됩니다.

해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

Gradient Boosting Machine

이번에 알아볼 그래디언트 부스팅 머신(Gradient Boosting Machine, GBM)은 경사 하강법(Gradient descent)을 결합한 새로운 부스팅(Boosting) 알고리즘입니다. Adaboost는 이전 약한 모델의 오답에 가중치를 부여하여 새로운 모델을 학습하는 방법이었는데요. 그래디언트 부스팅 머신은 잔차(Residual)에 집중합니다. 이 잔차를 최소화하는 과정에서 경사 하강법을 사용하기 때문에 이런 이름이 붙었습니다.

Residual

그래디언트 부스팅 머신이 작동되는 방식에 대해서 알아보겠습니다. 먼저 첫 번째 약한 모델(Weak Model) $f_1(\mathbf{x})$ 를 만듭니다. 다음으로 정답과 예측값의 차이, 즉 잔차 $R_1$ 을 계산합니다.

[y = f_1(\mathbf{x}) + R_1
R_1 = y - f_1(\mathbf{x})]

다음으로는 잔차 $R_1$ 을 예측하는 두 번째 약한 모델 $f_2(\mathbf{x})$ 을 만듭니다. 그리고 $R_1$ 과 $f_2(\mathbf{x})$ 의 잔차 $R_2$ 를 구합니다.

[R_1 = f_2(\mathbf{x}) + R_2
R_2 = R_1 - f_2(\mathbf{x})]

이렇게 $t$ 번째 약한 모델 $f_t(\mathbf{x})$ 는 $t-1$ 번째의 잔차를 근사하는 함수입니다. 이를 $T$ 번 반복한 뒤 정리하면 다음과 같은 식이 될 것입니다. 첫 $R_1$ 은 꽤 크지만 이를 반복해서 근사하는 모델을 더해나가면 마지막 잔차 $R_T$ 는 매우 작아집니다.

[y = f_1(\mathbf{x}) + f_2(\mathbf{x}) + \cdots + f_T(\mathbf{x}) + R_{T}]

만약 오차로 평균 제곱 오차(Mean square error, MSE)를 사용하는 회귀 문제라면 아래 이미지와 같이 생각해 볼 수도 있겠습니다.

이미지 출처 : github.com/topics/gradient-boosting-machine

반복 과정동안 잔차를 줄이는 것이 목적이므로 경사 하강법을 사용하여 잔차를 반복해서 줄여나갑니다. 아래는 Stump Tree를 약한 모델로 하는 그래디언트 부스팅 머신으로 회귀 함수를 근사하는 예시입니다. 아래는 1~3회 반복했을 때의 근사 함수와 잔차를 나타낸 이미지입니다.

이미지 출처 : medium.com/mlreview

낮은 반복수에서는 잔차가 꽤 크게 나오고 있습니다. 동일한 반복을 계속하면 함수 개형과 잔차가 어떻게 변하는 지 알아보겠습니다. 아래는 18~20회 반복했을 때의 근사 함수와 잔차를 나타낸 이미지입니다.

이미지 출처 : medium.com/mlreview

이전보다 잔차가 훨씬 더 줄어든 것을 볼 수 있습니다. 자세히 보면 함수도 좀 더 구불구불해진 것도 볼 수 있습니다. 동일한 과정을 50번 반복하면 아래와 같이 잔차가 더 줄어들고 함수도 더 복잡해집니다.

이미지 출처 : medium.com/mlreview

Loss Function

손실 함수(Loss function)의 기울기를 최소화하는 방향으로 추가적인 모델이 순차적으로 생성되기 때문에 어떤 손실 함수를 사용하는 지에 따라 최종으로 생성되는 함수가 달라집니다. 크게는 풀고자하는 문제가 회귀인지 분류인지에 따라서 다른 선택지를 갖게 됩니다.

Regression

회귀를 위한 손실 함수는 제곱 오차, 절대 오차, Huber 오차, Quantile 오차 등이 있습니다. 각각의 식은 아래와 같으며 일반적으로는 제곱 오차 $(L_2)$ 를 많이 사용합니다.

Huber 오차에서의 $\delta$ 와 Quantile 오차에서의 $\alpha$ 는 하이퍼파라미터로서 어떤 값을 지정하는지에 따라서 생성되는 함수의 개형이 달라집니다. 아래는 각 손실 함수의 개형과 싱크 함수(sinc function) ¹에 노이즈를 추가하여 생성한 데이터셋에 각 손실함수에 따라 생성되는 최종 함수를 비교한 결과입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

Classification

분류를 위한 손실 함수는 베르누이 오차, Adaboost 오차 등이 있습니다. 각각의 식은 아래와 같습니다. Adaboost와 마찬가지로 이진 분류시에 $y$ 의 레이블은 ${-1, 1}$ 로 합니다.

아래는 두 손실 함수의 개형을 나타낸 그래프입니다. Adaboost 손실 함수가 베르누이 손실 함수보다 더 빠르게 감소하는 것을 알 수 있습니다.

Regularization

그래디언트 부스팅 머신은 과적합(Overfitting)에 대한 문제를 가지고 있습니다. 정답 레이블을 $y$, 우리가 최종적으로 근사하고자 하는 함수를 $F(x)$, 소음으로 인해 발생하는 오차를 $\epsilon$ 이라 하면 $y = F(x) + \epsilon$ 으로 나타낼 수 있는데요. 근사하는 목적은 $F(x)$ 인데 반복수가 많아지다 보면 $\epsilon$ 까지 잔차로 인식해서 근사해버리는 과적합 문제가 발생합니다. 그래디언트 부스팅 머신의 과적합을 방지하기 위해서 적용하는 정칙화(Regularization) 방법에 대해 알아보겠습니다.

Subsampling

첫 번째 방법은 서브 샘플링(Subsampling)입니다. 이는 원래 데이터셋의 일부만을 추출하는 방법인데요. 원래의 데이터셋을 $D_0$ 이라 하면 이 데이터셋으로 첫 번째 약한 모델 $f_0$ 을 근사하게 되는데요. 다음 약한 모델 $f_1, \cdots$ 을 근사하기 위한 $D_1, \cdots$ 는 $D_0$ 를 전부 사용하지 않고 일부를 추출하는 방법입니다. 추출 방법으로는 기본적으로 비복원 추출을 기반으로 하고 있지만 복원 추출을 사용하여도 상관은 없습니다.

Shrinkage

수축법(Shrinkage)은 뒤쪽에 생성되는 모델의 영향력을 줄여주는 방법입니다. 아래 식에 있는 $\lambda$ 는 새로 생성되는 알고리즘의 영향을 얼마나 할 것인지를 정하는 하이퍼파라미터입니다. 이 값을 조정하여 뒤쪽에 생성되는 모델의 영향력이 줄어들면 뒤쪽에 생성되는 함수가 $\epsilon$ 까지 과하게 근사하지 못하도록 할 수 있습니다.

[\hat{f}t \leftarrow \hat{f}{t-1} + \color{red}{\lambda} \rho_t h(x, \theta_t)]

Early stopping

조기 종료(Early stopping)는 일반적으로 많이 사용되는 과적합 방지 방법입니다. 학습 오차와 검증 오차를 비교한 뒤에 검증 오차가 줄어들다가 다시 커지게 되면 반복을 종료하여 모델이 학습 데이터에 과적합 되는 현상을 막습니다.

Variable importance

랜덤 포레스트와 마찬가지로 그래디언트 부스팅 머신에서도 변수의 중요도를 측정할 수 있습니다. 일단 하나의 의사 결정 나무 $T$ 에서 변수 $j$ 의 중요도는 해당 변수를 사용했을 때 얻어지는 정보 획득량(Information gain, IG)을 모두 더하여 측정합니다. 수식으로 나타내면 아래와 같습니다. 아래 식에서 $L$ 은 해당 트리의 리프 노드의 개수이며 분기(Split) 횟수는 리프 노드 개수보다 1개 적기 때문에 $i = 1, \cdots, L-1$ 이 됩니다. $\mathbf{1}(S_i = j)$ 은 지시 함수(Indicator function)로 뒤 조건이 일치할 때는 $1$, 그렇지 않을 때는 $0$의 값을 가집니다. 여기서는 $i$ 번째 분기에 사용된 변수 $S_i$ 가 $j$ 가 동일할 때에만 $1$ 의 값을 나타냅니다.

[\text{Influence}j(T) = \sum^{L-1}{i=1} (IG_i \times \mathbf{1}(S_i = j))]

그래디언트 부스팅 머신에서 변수의 중요도는 각 트리마다 변수 $j$ 의 중요도를 평균내어 구합니다.

[\text{Influence}j = \frac{1}{M}\sum^{M}{k=1} \text{Influence}_j(T_k)]

Conclusion

Adaboost에 이은 새로운 부스팅 알고리즘인 그래디언트 부스팅 머신에 대해서 알아보았습니다. 그래디언트 부스팅 머신은 보다 좋은 성능을 보이지만 계속해서 근사 함수를 만들어 내야 하기 때문에 실행 시간이 오래 걸리고 많은 컴퓨팅 자원이 필요하다는 단점을 가지고 있습니다. 그래서 이후로 단점을 해결하기 위한 알고리즘이 계속해서 고안되었는데요. 다음에는 이를 개선한 XGBoost, LightGBM, CatBoost 등에 대해 알아보도록 하겠습니다.

해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

Boosting

이번에는 앙상블 방법 중 하나인 부스팅(Boosting)에 대해서 알아보고 부스팅의 시초격인 Adaboost(Adaptive Boosting)에 대해서 알아보도록 하겠습니다.

Weak Model

부스팅을 이해하기 위해서는 약한 모델(Weak Model)에 대해서 알아야 합니다. 약한 모델이란 말 그대로 성능이 낮은 모델을 가리킵니다. 약한 모델의 성능은 랜덤 추측(Random guessing)보다 약간 더 나은 수준이지요. 예를 들어, 이진 분류라면 랜덤 추측의 정확도는 약 $50\%$ 가 될 텐데요. 약한 모델의 정확도는 $60\%$ 정도가 되는 수준입니다. 우리가 성능 좋은 모델이라고 일컫는 $80\%$ 이상의 정확도를 보이는 모델보다는 확실히 성능이 떨어지지요.

부스팅은 약한 모델을 결합하면 임의의 강한 모델의 성능 이상으로 끌어올릴(Boosting) 수 있지 않을까 하는 아이디어에서 시작되었습니다. 먼저 약한 모델을 만든 후에 학습 결과를 바탕으로 이를 보완해 줄 수 있는 모델을 반복해서 생성합니다. 그리고 최종적으로 이를 결합한 모델을 만들어내지요. 잠시 다른 이야기로 빠져보겠습니다.

Weighted on wrong cases

학창 시절에 오답 노트를 만들어 보신 적이 있으신가요? 오답 노트는 틀린 문제를 모아 놓는 노트인데요. 완벽히 알고 푼 문제라면 다음에 다시 볼 필요가 없습니다. 틀린 문제를 중심으로 학습해야 점수가 오르겠지요. 예를 들어, 수능수학 범위에서 공부를 하다보니 ‘확률과 통계’ 단원이 약한 학생은 해당 단원의 문제가 오답 노트에 모입니다. 오답노트로 공부하다 보니 통계 단원은 금방 학습했는데 ‘확률’은 계속 틀립니다. ‘확률’ 단원의 문제가 계속 오답 노트에 모이게 되고 이를 바탕으로 학습하다 보니 이번에는 ‘중복조합’ 관련 문제를 계속 틀리네요. 이 학생은 이제 전체 수학에서 ‘중복조합’만 공부하면 되는 학생이 될 것입니다.

갑자기 이런 이유를 하는 이유는 부스팅 알고리즘이 학습하는 이유도 이와 유사하기 때문입니다. 일단 첫 번째 약한 모델이 학습 결과를 내놓으면 이를 바탕으로 오답 노트를 만듭니다. 두 번째 모델은 오답 노트를 바탕으로 공부하게 되며 이런 과정을 계속 반복하게 됩니다. 이와 같이 순차적으로 진행되기 때문에 병렬 처리(Parallel processing)가 불가능하다는 단점을 가지고 있습니다. 다만 Stump tree(결정 경계를 하나만 형성하는 의사 결정 나무)와 같은 약한 모델을 기반으로 하므로 결정 경계가 없어도 복잡도가 높은 모델을 사용하는 배깅보다 빠르게 학습이 진행되곤 합니다.

이미지 출처 : quantdare.com

Adaboost

Adaboost는 여러 부스팅 알고리즘 중에서 초기에 사용된 알고리즘 중 하나입니다. 해당 알고리즘은 틀리게 예측한 인스턴스에 가중치(Weight)를 부여한다는 아이디어를 기본으로 하고 있습니다. 특이한 점은 이진 분류 문제에서 레이블을 ${0, 1}$ 이 아니라 ${-1, 1}$ 로 구분한다는 것인데요. 이는 서포트 벡터 머신에서도 그랬듯이 알고리즘에서 사용되는 수식 때문입니다. 일단 이렇게 구분한다는 것만 염두에 두고 설명을 이어나가도록 하겠습니다.

가장 먼저 데이터셋을 준비합니다. 부스팅의 첫 번째 데이터셋은 배깅처럼 균일한 분포 $D_1(i)$ 로 구성합니다. 샘플링은 비복원 추출(Sampling without replacement)을 기본으로 하지만 복원 추출을 사용해도 됩니다. 이렇게 구성된 데이터셋을 바탕으로 학습을 진행하지요. $t(단, 1 \leq t \leq T)$ 번째 모델 $h_t$ 는 분포가 $D_t(i)$ 를 바탕으로 학습합니다. 일반적으로 약한 모델로는 Stump tree를 사용합니다.

$h_t$ 가 결과를 내놓으면 이를 바탕으로 $\epsilon_t$ 과 $\alpha_t$ 를 계산합니다. $\epsilon_t$ 는 훈련 데이터셋 중에서 $h_t$ 가 틀리게 판단한 데이터의 비율입니다. 예를 들어, 10개의 데이터 중 3개를 잘못 판단했다면 $\epsilon = 0.3$ 이 됩니다. 그리고 이 값을 아래 식에 대입하여 가중치 $\alpha_t$ 를 구합니다. (참고로 랜덤 추측보다 성능이 떨어질 경우 $\epsilon > 0.5$는 break 됩니다.)

[\alpha_t = \frac{1}{2} \ln \bigg(\frac{1 - \epsilon}{\epsilon}\bigg)]

$\alpha_t$ 값에 대해 좀 더 탐색해보겠습니다. 만약 $\epsilon_t \approx 0$, 즉 거의 모든 데이터가 제대로 판단되었다면 $\alpha_t$ 값은 매우 커지게 됩니다. 반대로 $e_t \approx 0.5$, 즉 랜덤 추측과 비슷한 상태라면 $\alpha_t$ 의 값은 $0$ 에 가까워지지요. 이렇게 구해진 $\alpha_t$ 는 $t+1$ 번째 학습에 사용될 데이터의 분포를 구하는 데 사용됩니다. $t+1$ 번째 학습에 사용될 데이터의 분포 $D_{t+1}(i)$ 는 다음과 같습니다.

[D_{t+1}(i) = \frac{D_t(i) \exp(-\alpha_t y_i h_t(x_i))}{Z_t}]

위 식에서 $Z_t$ 는 정규화를 위한 상수입니다. 분자의 각 항에 대해서 어떤 것을 의미하는 지 알아보겠습니다. 먼저 첫 번째 항은 $D_t(i)$ 입니다 $t+1$ 번째 데이터셋의 분포는 $t$ 번째 학습 데이터셋을 기반으로 함을 알 수 있습니다. 다음으로 $\exp$ 내에 있는 값을 하나씩 살펴보겠습니다. 일단 $\alpha_t$ 가 앞에 있네요. 해당 값에 대해서는 위에서 알아보았습니다. 마지막은 $y_ih_t(x_i)$ 입니다. 이 항은 ${-1, 1}$ 의 2가지 값을 가질 수 있습니다. 아래 수식을 보겠습니다.

[y_ih_t(x_i) = \begin{cases} 1 \qquad &\text{if} \quad y_i = h_t(x_i)
-1 \qquad &\text{if} \quad y_i \neq h_t(x_i) \end{cases}]

이 항은 정답 레이블과 예측 레이블 $(y_i, h_t(x_i))$ 이 동일한 경우 $(1,1) \text{ or } (-1,-1)$ 에는 $1$ 이 됩니다. 반대로 예측 레이블이 정답 레이블과 $(1,-1) \text{ or } (-1,1)$ 처럼 다르면 $-1$ 값을 나타내지요. 이제 $\exp(-\alpha_t y_i h_t(x_i))$ 값이 어떻게 변하는지 예측해 볼 수 있습니다. 아래 표를

일단은 틀리게 판단한 인스턴스에는 무조건 1보다 큰 값을 곱합니다. 그렇게 판단한 분류기가 성능이 좋을 수록 이 가중치는 커지게 되지요. 이런 인스턴스는 다음 분포에 포함될 확률이 높아집니다. 반대로 맞춘 인스턴스는 무조건 1보다 작은 값이 곱해집니다. 성능 좋은 분류기가 맞춘 경우에는 거의 0에 가까운 값이 곱해지며 다음 데이터셋에는 거의 포함될 확률이 낮아집니다.

이 과정을 $T$ 번 반복한 다음에는 각 단계에서 구해진 가중치 $\alpha_t$ 와 예측 레이블 $h_t(x)$ 를 모두 더하여 최종 레이블을 결정합니다. 즉 새로운 테스트 데이터 $(x^\prime, y^\prime)$ 에 대한 예측값은 아래와 같이 구합니다.

[H(x^\prime) = \text{sign}\bigg(\sum^T_{t=1} \alpha_t h_t(x^\prime)\bigg)]

Example

사실 글로만 이해하기에는 복잡한 알고리즘입니다. 예시를 바탕으로 Adaboost가 어떻게 작동하는 지 알아보도록 하겠습니다. 아래는 첫 번째 데이터셋의 분포인 $D_1$ 과 첫 번째 Stump tree인 $h_1$ 을 나타내고 있습니다. 그리고 이 결과에 따라 다음 데이터셋의 분포 $D_2$ 가 변하는 모습도 보여주고 있습니다.

이미지 출처 : cse.buffalo.edu

총 10개의 인스턴스 중 $h_1$ 이 잘못 판단한 인스턴스가 3개이므로 $\epsilon_1 = 3/10 = 0.3$ 입니다. 그리고 이를 대입하여 구하면 $\alpha_1 = 0.42$ 가 됩니다. $(e^{0.42} = 1.52, e^{-0.42} = 0.66)$ 이므로 정답과 예측 레이블이 일치하는 7개의 인스턴스는 $D_2$ 에서 덜 $(\times 0.66)$ 중요하게 샘플링되고, 불일치하는 3개의 인스턴스는 더 $(\times 1.52)$ 중요하게 샘플링됩니다.

이미지 출처 : cse.buffalo.edu

두 번째 결과에 대해서도 마찬가지로 판단합니다. 대신 2번째 부터는 가중치가 부여되어 추출되었으므로 정확히 개수로는 판단할 수 없고 위와 같은 결과 $\epsilon_2 = 0.21, \alpha_2 = 0.65$ 가 나왔다고 하겠습니다. $(e^{0.65} = 1.92, e^{-0.65} = 0.52)$ 이므로 정답과 예측 레이블이 일치하는 인스턴스는 $D_3$ 에서 덜 $(\times 0.52)$ 중요하게 샘플링되고, 불일치하는 인스턴스는 더 $(\times 1.91)$ 중요하게 샘플링됩니다.

이미지 출처 : cse.buffalo.edu

두 번째 결과에 대해서도 마찬가지로 판단합니다. 이 3개의 결과를 조합하면 다음과 같은 결정 경계가 만들어집니다.

이미지 출처 : cse.buffalo.edu

3개의 약한 모델(여기서는 Stump tree)을 결합하여 그럴듯한 결정 경계를 만들어냈습니다. 이 과정을 반복하면 다음과 더욱 정확한 모델을 만들어 낼 수 있습니다. 아래는 해당 과정을 50번 반복하면서 만들어지는 결정 경계를 시각화한 동영상입니다. 50번의 반복으로 비선형 결정 경계를 만든 것을 확인할 수 있습니다.

이미지 출처 : gfycat.com

Conclusion

이상으로 부스팅 알고리즘의 개요와 부스팅 알고리즘 중 하나인 Adaboost에 대해 알아보았습니다. 틀린 인스턴스에 가중치를 부여한다는 다소 간단한 아이디어를 적용했음에도 딥러닝 기법이 나오기 전까지 실시간 얼굴 추적(Real-time Face detection) 등 다양한 곳에 사용된 뛰어난 기법이기도 합니다. 다음 시간에는 새로운 부스팅 기법이자 XGBoost, LightGBM, CatBoost 등 최근 좋은 성능을 보이는 부스팅 알고리즘의 기반이 되는 그래디언트 부스팅 머신(Gradient Boosting Machine, GBM)에 대해 알아보도록 하겠습니다.

해당 게시물은 고려대학교 강필성 교수님의 강의를 바탕으로 작성한 것입니다.

Random Forest

랜덤 포레스트(Random Forest)는 자주 사용되는 앙상블 기법 중 하나입니다. 기본 모델로 의사 결정 나무(Decision tree)를 사용하기 때문에 배깅(Bagging)의 특수한 형태입니다. 배깅은 기본 모델로 무엇을 설정하든 상관없지만 랜덤 포레스트는 의사 결정 나무를 사용해야 합니다. 다수의 의사 결정 나무(Tree)를 결합한 모델이기에 Forest라는 이름이 붙었습니다.

이미지 출처 : unsplash.com

Why Random?

그렇다면 Forest 앞에 붙은 Random은 무슨 의미일까요? 변수를 임의(Random)로 선택한다는 뜻인데요. 이것이 랜덤 포레스트와 의사 결정 나무를 사용한 배깅의 차이점입니다. 원래의 의사 결정 나무는 결정 경계를 탐색할 때 모든 변수를 고려하여 정보 획득량(Information Gain, IG)이 가장 높은 지점을 찾아냅니다. 랜덤 포레스트는 이 중 일부의 변수만을 선택하여 정보 획득량이 최고인 지점을 탐색합니다.

아래는 25개의 변수 중에서 임의로 5개의 변수를 택할 때 변수가 어떻게 선택되는 지를 나타낸 그림입니다.

이미지 출처 : github.com/pilsung-kang/Business-Analytics-IME654

첫 번째 결정 경계를 만들 때에는 임의로 5개의 특성 $(x_2, x_{10}, x_{23}, x_{17}, x_9)$ 이 선택되었습니다. 하지만 Depth가 2일 때에는 각각 $(x_1, x_{13}, x_{21}, x_{11}, x_7), (x_{24}, x_{15}, x_2, x_7, x_{19})$ 이 선택된 것을 확인할 수 있습니다.

Effect

이렇게 변수를 랜덤하게 선택하는 이유는 무엇일까요? 오히려 의사 결정 나무의 성능이 떨어질 텐데 말이지요. 그 이유는 다양성에 있습니다. 배깅만을 적용한 트리는 데이터 셋은 조금 다를 수 있어도 모든 변수를 탐색하기 때문에 비슷한 모델이 생성될 확률이 매우 높습니다. 하지만 랜덤 포레스트는 매번 다른 특성을 고려하기 때문에 훨씬 더 다양한 모델을 만들어낼 수 있습니다.

이해를 도울 수 있는 예시를 들어보겠습니다. 아래는 A반과 B반 학생 3명의 성적을 나타낸 표입니다.

학생 각각의 평균은 A반이 월등히 높습니다. B반 학생들의 평균은 모두 72점인데 A반 학생들의 평균은 약 90점이나 됩니다. 하지만 3명이 머리를 맞대고 국어, 영어, 수학을 풀어야 하는 상황이라면 결과는 조금 다릅니다. 각 과목의 최고점을 모아보면 A반은 $(91, 92, 94)$ 점이고 B반은 $(96, 96, 96)$ 점입니다. 개개인의 퍼포먼스는 A반이 더 높지만 집단 지성의 관점에서 봤을 때에는 B반의 퍼포먼스가 더 높겠네요.

완전히 동일한 예시는 아니겠습니다만 랜덤 포레스트가 변수를 선택하여 사용하는 이유도 이와 유사합니다. 특정 변수를 제약함으로써 전체적인 성능은 떨어지더라도 몇몇 특성에 전문화된 의사 결정 나무를 최대한 많이 만들지요. 그리고 이들을 한데 모았을 때의 시너지 효과를 기대하는 것입니다.

Generalization Error

랜덤 포레스트는 트리의 개수(Population size)가 일정 수준 이상으로 커졌을 때 일반화 오차(Generalization error)를 구할 수 있습니다. 일반화 오차의 상한선(Upper bound)는 다음과 같이 결정됩니다.

[\text{Generalization error} \leq \frac{\bar{\rho}(1-s^2)}{s^2}]

위 식에서 $\bar{\rho}$ 는 각 트리 사이의 상관계수를 구한 뒤 평균을 구한 값입니다. $s^2$ 는 마진값으로, 이진 분류에서는 $\vert P(y=1) - P(y=0) \vert$ 이 됩니다. 개별 트리가 정확할수록 $s^2$ 이 커지기 때문에 일반화 오차는 감소합니다. 그리고 트리 사이의 상관관계가 적을수록 $\bar{\rho}$ 가 줄어들어 일반화 오차가 감소하게 됩니다.

Permutation Importance

랜덤 포레스트에서는 특정 변수의 중요도를 측정할 수 있습니다. 변수의 중요도를 측정하는 방식은 다음과 같습니다. 먼저 아무것도 건드리지 않을 때의 검증 오차(OOB Error)를 측정합니다. 이 값을 $e_i$ 로 나타내겠습니다. 중요도를 측정하고자 하는 변수를 섞어준(Permutation) 뒤에 검증 오차를 측정합니다. 이 값을 $p_i$ 로 나타내겠습니다.

즉, $p_i$ 는 해당 변수에 해당하는 값을 엉망으로 만든 뒤에 측정한 값입니다. 결정 경계를 형성할 때 해당 변수를 많이 사용했다면 $p_i$ 와 $e_i$ 의 차이가 커지겠지요. 그래서 모든 트리에 대해 $p_i - e_i$ 의 값을 구해주어 중요도를 측정합니다.

$m$ 번째 트리에서 두 값의 차이를 $d^m_i = p^m_i - e^m_i$ 라 하면 $i$ 번째 변수가 중요할수록 $d_i$ 의 평균은 증가하고, 분산은 작아집니다. 따라서 아래와 같이 해당 변수의 중요도 $v_i$ 를 구할 수 있습니다.

[\bar{d}i = \frac{1}{m}\sum^m{i=1}d_i^m, \quad s_i^2 = \frac{1}{m-1}\sum^m_{i=1}(d_i^m - \bar{d}_i)^2
\therefore v_i = \frac{\bar{d}_i}{s_i^2}]

이렇게 구한 $v_i$ 는 변수의 상대적인 중요도를 나타낼 뿐 절대적인 의미는 없습니다. $v_i$ 값이 높은 변수가 다른 변수에 대해 상대적으로 중요할 뿐이지요. 아래는 특정 데이터의 중요도를 구한 뒤 시각화한 예시입니다.

이미지 출처 : www.researchgate.net

Conclusion

의사 결정 나무를 활용한 배깅에 랜덤 변수 선택을 더하여 다양성을 극대화하는 랜덤 포레스트(Random forest)에 대해 알아보았습니다. 다음부터는 데이터셋이나 변수 설정에서 다양성을 확보하는 방법이 아닌 먼저 생성된 모델의 추정치로부터 또 다른 모델을 생성하여 다양성을 확보하는 부스팅(Boosting) 계열의 알고리즘에 대해서 알아보도록 하겠습니다.